Main

Quantum-information tasks requiring high-dimensional bipartite entanglement include teleportation using qudits10,11, generalized dense coding (that is, with pairs of entangled d-level systems; ref. 12) and some quantum key distribution protocols13. More generally, schemes such as quantum secret sharing14 and measurement-based quantum computation15 apply multiparticle entanglement. These are promising applications, especially in view of recent progress in the development of quantum repeaters (see ref. 16 and references therein). However, practical applications of such protocols are only conceivable when it is possible to experimentally prepare, and moreover detect, high-dimensional entangled states. Therefore, the ability to verify high-dimensional entanglement between physical qudits is of crucial importance. Indeed, much progress has generally been made on the generation and detection of high-dimensional entangled states (please see ref. 17 and references within).

Here we report the experimental investigation of high-dimensional, two-photon entangled states. We focus on photon orbital angular momentum (OAM) entangled states generated by spontaneous parametric down-conversion (SPDC), and demonstrate genuine high-dimensional entanglement using violations of generalized Bell-type inequalities6. Previously, qutrit Bell-type tests have been carried out using photon OAM to verify three-dimensional entanglement (see ref. 18 and references within). In addition to testing whether correlations in nature can be explained by local realist theories19, the violation of Bell-type inequalities may be used to demonstrate the presence of entanglement. Bell-type experiments have been carried out using two-dimensional subspaces of the OAM state space of photons20,21 and experimentalists have demonstrated two-dimensional entanglement using up to 20 different two-dimensional subspaces22. Careful studies have also been carried out to describe how specific detector characteristics bound the dimensionality of the measured OAM states in photons generated by SPDC using Shannon dimensionality23.

Our experimental study of high-dimensional entanglement is based on the theoretical work of Collins et al. 6, which was applied in experiments for qutrits encoded in the OAM states of photons18,24. We encode qudits using the OAM states of photons, with eigenstates defined by the azimuthal index ℓ. These states arise from the solution of the paraxial wave equation in its cylindrical co-ordinate representation, and are the Laguerre–Gaussian modes L Gp,ℓ, so called because they are light beams with a Laguerre–Gaussian amplitude distribution.

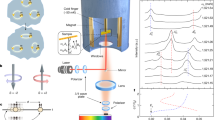
In our set-up (Fig. 1), OAM entangled photons are generated through a frequency-degenerate type-I SPDC process, and the OAM state is manipulated with computer-controlled spatial light modulators (SLMs) acting as reconfigurable holograms. Conservation of angular momentum ensures that, if the signal photon is in the mode specified by |ℓ〉, the corresponding idler photon can only be in the mode |−ℓ〉. Assuming that angular momentum is conserved9, a pure state of the two-photon field produced will have the form

where subscripts A and B label the signal and idler photons respectively, |cℓ|2 is the probability to create a photon pair with OAM ±ℓℏ and |ℓ〉 is the OAM eigenmode with mode number ℓ.

Figure 1: Schematic representation of experimental set-up for violations of Bell-type inequalities.
figure 1

C(Aa=v,Bb=w) or C(θAa,θBb) is the coincidence count rate when SLM A is in state |v〉aA or |θAa〉 and SLM B is in state |w〉bB or |θBb〉 respectively.

Full size image

It has been shown6 that, for correlations that can be described by theories based on local realism1, a family of Bell-type parameters Sd satisfies the inequalities

Alternatively, if quantum mechanics is assumed to hold, then the violation of an inequality of type (1) indicates the presence of entanglement. Sd can be expressed as the expectation value of a quantum mechanical observable, which we denote as . The expressions for Sd, and the operators and are provided in Supplementary Section SI.

The parameters Sd are calculated using coincidence probabilities for measurements made locally by two observers, Alice and Bob, on their respective subsystems, which in our case are the signal and idler photons from the SPDC source. Alice’s detector has two settings labelled by a∈{0,1} with d outcomes for each setting, and similarly for Bob’s detector with settings b∈{0,1}. The measurement bases corresponding to the detector settings of Alice and Bob are defined as

where v and w both run from 0 to d−1 and denote the outcomes of Alice’s and Bob’s measurements respectively, and the parameters α0=0, α1=1/2, β0=1/4 and β1=−1/4.

The measurement bases {|v〉aA} and {|w〉aA} have been shown5,25 to maximize the violations of inequality (1) for the maximally entangled state of two d-dimensional systems given by It turns out that we are able to parameterize these d-dimensional measurement basis states with ‘mode analyser’ angles θA and θB, and write them in the form

where

The function g(ℓ) is defined as

where [x] is the integer part of x, and u(ℓ) is the discrete unit step function.

Figure 2 shows an example of the experimental data points for the self-normalized coincidence rates as function of the relative angle (θA−θB) using d=11 (see also Supplementary Fig. S1). For a maximally entangled state

where h(ℓ)=1 for all ℓ when d is odd, and h(ℓ≠0)=1, h(0)=1 when d is even, the coincidence rate of detecting one photon in state |θA〉 and the other in state |θB〉 is proportional to

Figure 2: Coincidence count rate (self-normalized) as a function of the relative orientation angle between state analysers (θA−θB).
figure 2

Equation (5) for a state with maximal 11-dimensional entanglement is fitted to the experimental data with the vertical offset and amplitude left as free parameters. Errors were estimated assuming Poisson statistics.

Full size image

The key result of our paper is shown in Fig. 3, which shows a plot of experimental values of parameter Sd as a function of the number of dimensions d. The plot compares theoretically predicted violations for a maximally entangled state, the experimental readings and the local hidden variable (LHV) limit. The maximum possible violations (shown in Supplementary Table S1) are slightly larger than the corresponding violations produced by a maximally entangled state. Violations persist up to as much as d=12 when entanglement concentration26 is applied. We find S11=2.39±0.07 and S12=2.24±0.08, which clearly violate Sd≤2 (see also Supplementary Table S4). In the corresponding experiment using L Gp,ℓ modes with only p=0, violations are obtained up to d=11. Without entanglement concentration, we observe violations only up to d=9 (please see Supplementary Fig. S2 in Section SIV). Above d∼11, the strength of the signal becomes so low that noise begins to overshadow the quantum correlations. In Fig. 2, the theoretical prediction in equation (5) for a state with maximal 11-dimensional entanglement is fitted to the experimental coincidence data obtained using the mode analyser settings defined in equation (4) for d=11, with only the vertical offset and amplitude left as free parameters. The observed fringes are seen to closely match those theoretically obtained for a state with maximal 11-dimensional entanglement.

Figure 3: Experimental Bell-type parameter Sd versus number of dimensions d.
figure 3

Sd>2 violates local realism for any d≥2. The plot compares the theoretically predicted violations by a maximally entangled state and the LHV limit with the experiments. Violations are observed for up to d=12. Errors were estimated assuming Poisson statistics.

Full size image

The violation of a Bell inequality in d×d dimensions directly indicates that the measured state was entangled. It remains to determine how many dimensions were involved in the entanglement. Measuring the coincidence probabilities, that is, of there being the joint state (Fig. 4), together with the parameters Sd for different d, can be seen as a partial tomography of the SPDC source state. Numerical investigations indicate that a state with the experimentally observed coincidence probabilities and parameters S2,S3,…,S11 must contain genuine 11-dimensional entanglement. In other words, it is not possible to obtain the observed levels of violation with a state that contains entanglement involving only 10 dimensions or less. Our analysis assumes a special form of the states, based on the coincidence measurement results shown in Fig. 4. Further details are given in Supplementary Section SII.

Figure 4: Experimental coincidence rates proportional to the probability of measuring the state with ℓs,ℓi=−5,…,+5.
figure 4

The coloured and greyed-out bars depict the measurement results with and without the application of Procrustean filtering respectively. The measurement time was 20 s for each combination of ℓs and ℓi.

Full size image

Our results hold much promise for applications requiring entangled qudits in general. As mentioned earlier, progress in the development of quantum repeaters (see ref. 16 and references therein) would make quantum key distribution using high-dimensional entangled states13 a possible application. Conventional quantum communication will fail for sufficiently large transmission distances because of loss, and quantum repeaters are one possible solution to this problem. Although experimental quantum key distribution has been demonstrated with OAM qutrits24, our findings provide experimental evidence that such protocols could be implemented using photons entangled in OAM in up to 11 dimensions, resulting in a considerable increase in information coding density.

A possible extension to our work would be to investigate the generation of multiphoton, high-dimensional OAM entanglement. We can conceive of achieving this using a cascade of down-conversion crystals for generating multipartite entangled photons, which has been done for polarization entangled photons17. It also seems to be within reach to combine the high-dimensional photon OAM entanglement with entanglement in the polarization and path degrees of freedom, creating even larger hyper-entangled states (see ref. 17 and references within).

On a more fundamental note, Bell test experiments carried out so far have one or both of two main loopholes, namely the locality and detection loopholes. However, a recent theoretical work reveals that even low-dimensional qudits can provide a significant advantage over qubits for closing the detection loophole5. In fact, it was found that as much as 38.2% loss can be tolerated using four-dimensional entanglement. Our results raise interesting possibilities regarding the role higher-dimensional entangled qudits could play in closing this loophole. We emphasize that neither the detection nor the locality loophole has been closed in our experiments, because the overall efficiency of our experimental set-up is 1–2%, and the switching time for our measurement devices (SLMs) is of the order of tens of milliseconds. However, closing these loopholes was not the immediate goal of our experiments. We are instead using the violation of Bell inequalities, up to fair sampling assumptions, as a means of verifying the presence of high-dimensional entanglement, within the framework of quantum mechanics.

In summary, we have been able to experimentally demonstrate violations of Bell-type inequalities generalized to d-dimensional systems6 with up to d=12, enough to indicate genuine 11-dimensional entanglement in the OAM of signal and idler photons in parametric down-conversion. It seems that this could be extended to even higher dimensions by using a brighter source of entangled photons.

Methods

In our experiments, we use computer-controlled SLMs (Hamamatsu) operating in reflection mode with a resolution of 600×600 pixels. In the detection, the SLMs are prepared in the states defined in equation (4) respectively. An SLM prepared in a given state transforms a photon in that state to the Gaussian |ℓ=0〉 mode. The reflected photon is then coupled into a single-mode fibre which feeds a single photon detector. As only the |ℓ=0〉 mode couples into the fibre, a count in the detector indicates a detection of the state in which the SLM was prepared. The hologram generation algorithm introduced in ref. 27 is applied to configure the SLMs.

Figure 1 shows a schematic diagram of the experimental set-up as well as examples of SLM settings used where d=1. For the SPDC, we use a pump beam, with ℓ=0, produced by a frequency-tripled, mode-locked Nd-YAG laser with an average output power of 150 mW at 355 nm. The collimated laser beam is normally incident on a 3-mm-long β-barium borate (BBO) crystal cut for type-I collinear phase matching. A 50:50 beam splitter (BS) then separates the co-propagating OAM entangled photons probabilistically into the signal and idler paths. Spectral filters with 10 nm bandwidth are used to reduce the detection of noise photons. The coincidence resolving time is 10 ns and an integration time of 20 s is used for the measurements.

For tests within a d-dimensional subspace and for odd d, we choose the modes ℓ=−(d−1)/2,…,0,…,(d−1)/2 as the computational basis states |j〉 in equations (2) and (3), where j=0,…,d−1. For even d, we use ℓ=−d/2,…,−1,1,…,d/2, omitting the ℓ=0 mode. A projection of the SPDC output state onto a d-dimensional subspace results in a non-maximally entangled state owing to the limited spiral bandwidth28. To enhance the entanglement, we use the so-called Procrustean method of entanglement concentration26. This is generally done by means of a filtering technique that equalizes the mode amplitudes, thereby probabilistically enhancing the entanglement of the two-photon state29. This can be achieved by applying local operations to one or both of the signal and idler photons. We choose local operations matched to the spiral bandwidth measurement for our SPDC source (please see Supplementary Section SIV), so as to obtain a close approximation to a maximally entangled state. The method applied in ref. 30 uses lenses for equalizing amplitudes in a superposition of three OAM modes. We however use alterations of the diffraction efficiencies of blazed phase gratings in the SLMs to achieve this goal for up to 14 modes. Figure 4 contrasts the results of coincidence measurements with and without Procrustean filtering, with the SLMs in the state where ℓA,ℓB∈{−5,…,+5}. The disadvantage of the Procrustean method is the associated reduction in the number of detected photons (see Supplementary Section SIII for further details).