Main

The possibility of a phase transition between two forms of the liquid phase in some pure substances has attracted considerable interest and research activity in recent years1,2,3,4,5,6,7,8,9,10. Among the substances investigated are water6,8,9, silica10, silicon1,11,12,13,14,15,16,17, germanium, carbon and hydrogen—these substances together form a very significant component of our natural world, living organisms and technology. A phenomenon common to these is therefore of wide general interest. Furthermore, as illustrated in ref. 18, liquid–liquid transitions offer an avenue for interesting applications that exploit the different properties of distinct liquid phases.

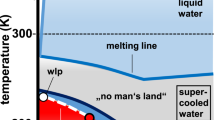
Although the liquid–liquid phase transition (LLPT) had been discussed in the context of silicon11 earlier, the considerable current interest stems from various proposals for understanding the anomalies of water2,4,6,7,8,19,20. These scenarios have alternately invoked the approach to a spinodal4, a liquid–liquid critical point6,8, general thermodynamic constraints without the presence of any singular behaviour7, and the presence of a transition without a critical point2, in rationalizing experimentally observed behaviour. In spite of substantial investigations, a general consensus has still to be reached on the interpretation of the observed behaviour2,19. In particular, recent experiments on confined water20 and issues surrounding their interpretation2 indicate the need to ascertain the existence of a critical point even when sufficient evidence exists for a liquid–liquid transition.

The possibility of a transition in supercooled silicon was suggested12 on the basis of estimates of the excess Gibbs free energies of amorphous and liquid silicon, implying an ‘amorphous-liquid’ phase transition near 1,450 K (below the freezing point of the liquid, 1,685 K). Clear evidence of a transition between two liquids in the supercooled region was shown in ref. 1 from molecular dynamics simulations using the Stillinger–Weber (SW) potential21. A first order transition at zero pressure was found at T=1,060 K, substantially below the experimental estimate. However, recent electrostatic levitation experiments performed down to T=1,382 K have not found evidence for a transition22. Apart from the uncertainties in the experimental value, such a difference may be expected to arise from the neglect in the empirical potential of significant changes in the electronic structure associated with structural change16,17, although first principles simulations17 appear to confirm the transition temperature obtained from the classical simulations. Furthermore, a recent experimental investigation of the LLPT in silicon using femtosecond pump–probe spectroscopy by Beye et al.23,24 observed electronic structure features similar to those in ref. 16, although without precise temperature measurements.

A detailed comparison of experimental data (to be described elsewhere) indicates that the SW potential captures qualitatively, and to a large degree quantitatively, the changes in the structure and thermodynamics of silicon in the liquid state, albeit with noticeable shifts in the themophysical properties (for example the density). We therefore expect the results obtained with the SW potential to give a good representation of the behaviour of real silicon, but with shifts in the temperature and pressure of the transition. Keeping this in mind, along with the large uncertainty and scarcity of experimental data, the precise location of the transition must be viewed as tentative at present, requiring further investigation to determine it precisely.

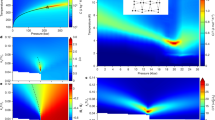
In the present work, we carry out molecular dynamics (MD) simulations using the SW potential for silicon to locate the liquid–liquid critical point, and show that it lies at negative pressures. We perform constant pressure and temperature (NPT) and constant volume and temperature (NVT) simulations of 512 atoms, using the protocols described in Methods. Pressure versus density isotherms generated in the temperature range 1,070–1,510 K, and the pressure range −3.8 GPa to +3.8 GPa using NPT simulations are shown in Fig. 1a. The isotherms for temperatures above T=1,133 K are continuous, but develop an inflection below T=1,259 K, which becomes more pronounced as the temperature is lowered. The compressibility develops a maximum in this temperature range, which grows as the temperature is lowered. Below T=1,108 K, careful constant pressure simulations always result in a jump in the density as the pressure is varied, suggesting a first order transition. To verify this further, we perform NVT simulations for T=1,108 K,1,082 K and 1,070 K in the density range where NPT simulations show a jump. These results are shown in Fig. 1b. We find that at these temperatures, the isotherms are non-monotonic. Such non-monotonicity in the simulations arises, on the one hand, from metastability, and on the other hand, from incomplete phase separation owing to finite sample sizes in the unstable region, and constitutes a clear indication of a first order transition. Thus, our equation of state data show isotherms with growing compressibility maxima as the temperature is decreased (above T=1,133 K) and first order transitions (below T=1,108 K) between two liquids, the high density liquid (HDL) and the low density liquid (LDL). We thus deduce that the critical point is located between these temperatures. Inspection of Fig. 1b also makes it clear that the critical pressure must be negative. Based on the above data at the temperatures simulated, we estimate the location of the critical point to be at Tc∼1,120±12 K, Pc∼−0.6±0.15 GPa. A more precise estimation of the critical parameters requires an analysis, including finite-size scaling, that is beyond the scope of the present paper, but is being pursued as an extension of the present work.

Figure 1: Equation of state.
figure 1

a, Pressure versus density isotherms from NPT simulations. Isotherms for T≥1,133 K are continuous, and the lines through the data points are polynomial fits used to obtain the compressibility. For 1,133 K≤T≤1,259 K, the isotherms show an inflection, corresponding to a compressibility maximum. For T<1,133 K, the isotherms show a density discontinuity, signalling a first order transition. The crossing of isotherms at positive pressures reflects the presence of density maxima. b, Pressure versus density below the critical point from NPT (open symbols) and NVT (filled symbols) simulations. Pressures from NVT simulations below T=1,133 K exhibit non-monotonic behaviour at intermediate densities, indicating a phase transition, although matching with pressures from NPT simulation at high and low densities. The critical temperature lies between T=1,133 K and T=1,108 K. (Error bars in all figures are calculated from (a minimum of three) independent samples, as σ/(n1/2), where σ is the standard deviation and n is the number of samples.)

Full size image

Approaching the critical point from above leads to increased density fluctuations. In addition to evaluating the compressibility from the equation of state (EOS), we also calculate it directly from density fluctuations. These are shown in Fig. 2 for temperatures above T=1,133 K and show good agreement with EOS estimates for the high density liquid, but poorer agreement for the low density liquid. The high crystallization rates observed near, and at lower pressures than, the compressibility maxima hamper improved sampling (however we report results only from equilibrated runs). The influence of fluctuations and local structure (see below) on nucleation rates25,26 is an interesting issue that is being investigated at present.

Figure 2: Compressibility maxima increase with decrease in temperature.
figure 2

Compressibilities KT versus pressure for different temperatures from NPT simulations. The lines show KT calculated from the derivative of the pressure along isotherms and the symbols show KT calculated from volume fluctuations. The maximum value of KT increases as temperature decreases, indicating an approach to a critical point.

Full size image

Next we describe briefly the temperature and density dependence of diffusivities D and average coordination number (the number of neighbouring atoms in the first coordination shell; see Methods) Nn, which captures important information regarding structural change. In Fig. 3a, Nn is shown as a function of pressure. At high temperatures and pressures, Nn is approximately 5, and decreases as temperature and pressure are lowered, showing a discontinuous change below 1,133 K, with values close to the tetrahedral value of 4 (∼4.1) in the LDL, similar to the observation at zero pressure in ref. 1.

Figure 3: Coordination number and diffusivity.
figure 3

a, Coordination number Nn against pressure for different temperatures as obtained from NPT simulations. In the HDL, Nn is approximately five. In the LDL, Nn approaches four, corresponding to a tetrahedral local structure. b, Diffusivity D against pressure for different temperatures. D is calculated from the mean square displacement, and shows a dramatic drop of over two orders of magnitude as the liquid transforms from the HDL to the LDL.

Full size image

Diffusivities versus pressure for the temperatures studied are shown in Fig. 3b, which increase with pressure for all the temperatures shown, in analogy with the well-known anomaly in water. Similar to coordination number, diffusivities show a discontinuity below T=1,133 K, with a jump of roughly two orders of magnitude from the HDL to the LDL. The diffusivities span a range of over four orders of magnitude.

In Fig. 4, we show the diffusivities D plotted against coordination number Nn. Except at the highest temperature studied, we find the dependence of D on Nn to be remarkably similar irrespective of temperature, including those below the critical temperature. Therefore, the mobility of atoms is very strongly determined by the local structure. This observation is consistent with a previous analysis of the role of ‘bifurcated bonds’ or the ‘fifth neighbour’ in determining molecular mobility in water27. It is tempting to speculate that, apart from trivial thermal effects, a universal dependence exists for atomic mobility on the average number of neighbours in excess of the tetrahedral value of 4. To test this possibility, we show in the inset of Fig. 4 a scaled plot of D, by normalizing to its value at a fixed Nn in the HDL phase for all temperatures. The remarkable data collapse, not previously demonstrated, spans two distinct phases, a wide range of temperature and pressure, and four decades of change in diffusivity. The resulting master curve can be fitted well to a Vogel–Fulcher–Tammann (VFT) form, D(n)=D0exp(−A/(n−n0)), with n0=3.86, and also to a power law D(n)=(n−n0)3, with n0=4.06. Further analysis of this interesting observation is in progress.

Figure 4: Relationship between structure and dynamics.
figure 4

Diffusivity D against coordination number Nn at different temperatures. Lines through the data points are guides to the eye, and highlight the remarkably similar dependence of D on Nn at all temperatures, including those below the critical temperature, where both D and Nn change discontinuously. (Inset) Plot of D (scaled to match at Nn=4.8) versus Nn, showing data collapse. The solid line is a Vogel–Fulcher–Tammann (VFT) fit, with a coordination number of vanishing diffusivity=3.86. The dashed line is a power law fit, with a coordination number of vanishing diffusivity =4.06.

Full size image

Previous studies of the phase behaviour of water and other liquids exhibiting density anomalies have analysed the interplay of various loci of extremal behaviour, namely the spinodal, lines of density maxima (TMD; ref. 4), density minima (TMinD; refs 28, 29), and compressibility minima (TMinC) and maxima (TMC). To obtain a comprehensive picture of the phase behaviour of liquid silicon, we have evaluated these loci, employing, in addition to the MD simulations, parallel tempering (PT) and restricted ensemble (REMC) Monte Carlo simulations to locate the spinodal (details and data are provided in the Supplementary Information) at low temperatures. As shown in Fig. 5, the spinodal we estimate is monotonic in pressure versus temperature T, meaning that it is not ‘reentrant’, as predicted to be the case4 if it intersects with the TMD. The TMD, however, changes slope on intersection with the TMinC, as analysed in ref. 7. Evaluating the relevant equation of state data is particularly challenging in this case, as the TMD approaches the spinodal very closely, but does not intersect it. From available data, it appears that the TMinC will join smoothly with the TMC (line of compressibility maxima) that emanates from the liquid–liquid critical point. Interestingly, we find from PT simulations below the critical temperature and pressure that there exists also a line of density minima, very recently observed in the case of water in experiments and computer simulations28,29. The TMD and the TMinD appear to join smoothly with each other, as required by thermodynamic consistency.

Figure 5: Phase diagram in PT plane.
figure 5

The pressure–temperature phase diagram showing the location of the liquid-crystal phase boundary32, the liquid–gas phase boundary and critical point, the liquid–liquid phase boundary and critical point, the liquid spinodal, the tensile limit obtained from two different increasing tensile pressure at two different rates, the density maximum (TMD) and minimum (TMinD) lines, and the compressibility maximum (TMC) and minimum (TMinC) lines. Lines joining TMD and TMinD (dot–dashed), TMC and TMinC (dashed) are guides to the eye. (Inset) Enlargement of box in main panel showing that TMD and spinodal lines do not intersect.

Full size image

At low temperatures T (1,440 K<T<2,000 K), even REMC simulations (which restrict density fluctuations) cavitate at sufficiently low pressure. In these cases, we estimate the spinodal by a quadratic extrapolation of the isotherms. As a further check on our spinodal estimate, we perform simulations to obtain tensile limits, by increasing the tensile pressure on the simulation cell at constant rates, for two different rates (0.1 and 10.0 MPa ps−1). For the faster rate, we find tensile limits that are consistent with our spinodal estimates, whereas for the slower rate, the system cavitates at higher pressures, remaining nevertheless monotonic versus temperature. These simulations also extend our estimate of the spinodal to lower temperatures, and indicate a marked downturn of the spinodal pressure below the temperatures we have studied.

In conclusion, we have performed extensive molecular dynamics and Monte Carlo simulations of supercooled liquid silicon using the SW potential, and, for the first time, we provide evidence for a negative pressure liquid–liquid critical point. We estimate the location of the critical point to be at Tc∼1,120±12 K, Pc∼−0.60±0.15 GPa. We have computed the phase diagram of supercooled liquid silicon. We find no retracing of the spinodal. The phase behaviour of silicon is similar to that observed in simulations of water and silica. The structure of the liquid changes dramatically in going from high temperatures and pressures to low temperatures and pressures. Diffusivities vary by more than four orders of magnitude and exhibit an anomalous pressure dependence. A strong relationship between local geometry, quantified by the coordination number, and diffusivity is seen, suggesting that atomic mobility in both low and high density liquids can usefully be analysed in terms of defects in the tetrahedral network structure.

Methods

We perform MD simulations, with a time step of 0.383 fs, with details as in ref. 1, but employing an efficient algorithm30 for energy and force evaluations. NVT simulations employ the LAAMPS (ref. 31) parallelized MD package. PT and REMC Monte Carlo simulations are described in the Supplementary Information.

In the HDL phase, a minimum of 3–6 independent samples are simulated for ∼100 relaxation times (∼10 ns). In the LDL phase, crystallization (monitored by energy jumps, mean square displacement (MSD) and the pair correlation function) rates are high. We perform around 10–50 initial runs, each of 22 ns. Non-crystallizing samples (an average of 5) were run for up to 10 relaxation times when possible. In all LDL cases, simulations are carried out for the time required for the MSD to reach 1 nm2 (5σ2, where σ is the atomic diameter) or for 100 ns (300 million MD steps), whichever is the larger.

Equilibration is monitored by the MSD and the overlap function Q(t), defined as , where w(r)=1, if r≤0.3σ, zero otherwise. We evaluate relaxation times (τ) by fitting Q(t) to a stretched exponential function. As an indication of its variation, τ varies at P=0 GPa in the HDL phase from 0.3 ps T=1,260 K) to 0.01 ns (T=1,068 K). In the LDL phase at T=1,060 K the value of τ is around 30 ns.

We calculate the compressibility KT from the EOS using:

where ρ is the number density and P is the pressure. Polynomial fits to isotherms are used in calculating the derivatives. We also calculate KT from fluctuations of volume V (NPT simulations) using:

The latter method is computationally very demanding, and the comparison between the two reveals the degree to which sampling is satisfactory. In the HDL the two estimates of KT agree very well, but in LDL, below the KT maximum, the deviations between the two indicate that sampling in the LDL is not sufficient to obtain KT from fluctuations.

The coordination number, Nn, is calculated by integrating the pair correlation function g(r) up to its first minimum. Note that in ref. 1 the integration was performed up to the first minimum of n(r)=ρ4π r2g(r), rather than the g(r) directly, which leads to a small underestimate in the coordination number at high temperatures and pressures.