Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology

Nature Physics volume 7, pages 406–411 (2011)Cite this article

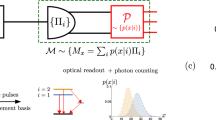
Abstract

The estimation of parameters characterizing dynamical processes is central to science and technology. The estimation error changes with the number N of resources employed in the experiment (which could quantify, for instance, the number of probes or the probing energy). Typically, it scales as . Quantum strategies may improve the precision, for noiseless processes, by an extra factor . For noisy processes, it is not known in general if and when this improvement can be achieved. Here we propose a general framework for obtaining attainable and useful lower bounds for the ultimate limit of precision in noisy systems. We apply this bound to lossy optical interferometry and atomic spectroscopy in the presence of dephasing, showing that it captures the main features of the transition from the 1/N to the behaviour as N increases, independently of the initial state of the probes, and even with use of adaptive feedback.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Set-ups for quantum parameter estimation.
Figure 2: Lower bounds for the phase error.
Figure 3: Numerical test of the tightness of the bound.

Similar content being viewed by others

References

  1. Bolinguer, J. J. et al. Optimal frequency measurements with maximally correlated states. Phys. Rev. A 54, R4649–R4652 (1996).

    Article  ADS  Google Scholar 

  2. Lee, H., Kok, P. & Dowling, J. P. A quantum Rosetta stone for interferometry. J. Mod. Opt. 49, 2325–2338 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  3. Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: Beating the standard quantum limit. Science 306, 1330–1336 (2004).

    Article  ADS  Google Scholar 

  4. Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  5. Kołodyński, J. & Demkowicz-Dobrzański, R. Phase estimation without a priori phase knowledge in the presence of loss. Phys. Rev. A 82, 053804 (2010).

    Article  ADS  Google Scholar 

  6. Knysh, S., Smelyanskiy, V. N. & Durkin, G. A. Scaling laws for precision in quantum interferometry and the bifurcation landscape of the optimal state. Phys. Rev. A 83, 021804(R) (2011).

    Article  ADS  Google Scholar 

  7. Helstrom, C. W. Quantum Detection and Estimation Theory (Academic, 1976).

    MATH  Google Scholar 

  8. Holevo, A. S. Probabilistic and Statistical Aspects of Quantum Theory (North-Holland, 1982).

    MATH  Google Scholar 

  9. Cramér, H. Mathematical Methods of Statistics (Princeton Univ., 1946).

    MATH  Google Scholar 

  10. Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2001).

    MATH  Google Scholar 

  11. Kraus, K. States, Effects, and Operations: Fundamental Notions of Quantum Theory (Springer, 1983).

    Book  Google Scholar 

  12. Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439–3443 (1994).

    Article  ADS  MathSciNet  Google Scholar 

  13. Braunstein, S. L., Caves, C. M. & Milburn, G. J. Generalized uncertainty relations: Theory, examples, and Lorentz invariance. Ann. Phys. (N.Y.) 247, 135–173 (1996).

    Article  ADS  MathSciNet  Google Scholar 

  14. Boixo, S., Flammia, S. T., Caves, C. M. & Geremia, J. M. Generalized limits for single-parameter quantum estimation. Phys. Rev. Lett. 98, 090401 (2007).

    Article  ADS  Google Scholar 

  15. Monras, A. & Paris, M. G. A. Optimal quantum estimation of loss in bosonic channels. Phys. Rev. Lett. 98, 160401 (2007).

    Article  ADS  Google Scholar 

  16. Dorner, U. et al. Optimal quantum phase estimation. Phys. Rev. Lett. 102, 040403 (2009).

    Article  ADS  Google Scholar 

  17. Demkowicz-Dobrzański, R. et al. Quantum phase estimation with lossy interferometers. Phys. Rev. A 80, 013825 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  18. Sarovar, M. & Milburn, G. J. Optimal estimation of one-parameter quantum channels. J. Phys. A 39, 8487–8505 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  19. Huelga, S. F. et al. Improvement of frequency standards with quantum entanglement. Phys. Rev. Lett. 79, 3865–3868 (1997).

    Article  ADS  Google Scholar 

  20. Dowling, J. P. Correlated input-port, matter-wave interferometer: Quantum noise limits to the atom-laser gyroscope. Phys. Rev. A 57, 4736–4746 (1998).

    Article  ADS  MathSciNet  Google Scholar 

  21. Higgins, B. L. et al. Entanglement-free Heisenberg-limited phase estimation. Nature 450, 393–396 (2007).

    Article  ADS  Google Scholar 

  22. Shaji, A. & Caves, C. M. Qubit metrology and decoherence. Phys. Rev. A 76, 032111 (2007).

    Article  ADS  Google Scholar 

  23. Huver, S. D., Wildfeuer, C. F. & Dowling, J. P. Entangled Fock states for robust quantum optical metrology, imaging, and sensing. Phys. Rev. A 78, 063828 (2008).

    Article  ADS  Google Scholar 

  24. Banaszek, K., Demkowicz-Dobrzański, R. & Walmsley, I. Quantum states made to measure. Nature Photon. 3, 673–676 (2009).

    Article  ADS  Google Scholar 

  25. Kacprowicz, M. et al. Experimental quantum-enhanced estimation of a lossy phase shift. Nature Photon. 4, 357–360 (2010).

    Article  ADS  Google Scholar 

  26. Fujiwara, A. & Imai, H. A fibre bundle over manifolds of quantum channels and its application to quantum statistics. J. Phys. A 41, 255304 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  27. Caves, C. M. Quantum-mechanical radiation-pressure fluctuations in an interferometer. Phys. Rev. Lett. 45, 75–79 (1980).

    Article  ADS  Google Scholar 

  28. Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981).

    Article  ADS  Google Scholar 

  29. Ou, Z. Y. Fundamental quantum limit in precision phase measurement. Phys. Rev. A 55, 2598–2609 (1997).

    Article  ADS  Google Scholar 

  30. Ulam-Orgikh, D. & Kitagawa, M. Spin squeezing and decoherence limit in Ramsey spectroscopy. Phys. Rev. A 64, 052106 (2001).

    Article  ADS  Google Scholar 

  31. André, A., Sorensen, A. S. & Lukin, M. D. Stability of atomic clocks based on entangled atoms. Phys. Rev. Lett. 92, 230801 (2004).

    Article  ADS  Google Scholar 

  32. Uhlmann, A. The ‘transition probability’ in the state space of a *-algebra. Rep. Math. Phys. 9, 273–279 (1976).

    Article  ADS  MathSciNet  Google Scholar 

  33. Berry, D. W. & Wiseman, H. M. Optimal states and almost optimal adaptive measurements for quantum interferometry. Phys. Rev. Lett. 85, 5098–5101 (2000).

    Article  ADS  Google Scholar 

  34. Armen, M. A. Adaptive homodyne measurement of optical phase. Phys. Rev. Lett. 89, 133602 (2002).

    Article  ADS  Google Scholar 

  35. Hentschel, A. & Sanders, B. C. Machine learning for precise quantum measurement. Phys. Rev. Lett. 104, 063603 (2010).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors acknowledge financial support from the Brazilian funding agencies CNPq, CAPES and FAPERJ. This work was performed as part of the Brazilian National Institute of Science and Technology for Quantum Information.

Author information

Authors and Affiliations

  1. Instituto de Física, Universidade Federal do Rio de Janeiro, Rio de Janeiro (RJ), 21941-972, Brazil

    B. M. Escher, R. L. de Matos Filho & L. Davidovich

Authors
  1. B. M. Escher
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. L. de Matos Filho
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. L. Davidovich
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed substantially to this work.

Corresponding author

Correspondence to B. M. Escher.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 452 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Escher, B., de Matos Filho, R. & Davidovich, L. General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology. Nature Phys 7, 406–411 (2011). https://doi.org/10.1038/nphys1958

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys1958

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing