Main

Below the Néel temperature, of the order of 150 K, the parent compounds of the iron pnictide superconductors remain metallic with a magnetization density oscillating in space (spin density wave, SDW). The sublattice magnetization is concentrated on iron atoms and its arrangement in space is antiferromagnetic in the x direction and ferromagnetic in the y direction7.

We use the combination of density functional theory and dynamical mean-field theory (DFT+DMFT; ref. 8) to theoretically study the archetypical iron pnictide compound BaFe2As2 in both the magnetic SDW and the paramagnetic (PM) state. The size of the theoretical magnetic moment is 0.90(5) μB, similar to the measured moment of 0.87(3) μB (ref. 9), but much smaller than 1.75 μB (ref. 10) obtained by the local spin density approximation (LSDA) within DFT. The considerably smaller magnetic moment obtained here is due to the fact that the competing PM metallic state is a correlated metal, which contains very fast fluctuating moments in time, but no static moment. Only a small fraction of these fluctuating moments acquire a static component in the ordered state.

The onset of magnetic order has a profound impact on the electronic structure, and these changes are probed by optical spectroscopy. Figure 1a shows the in-plane (averaged over x and y directions) optical conductivity of BaFe2As2 in the SDW and PM states calculated by both DFT+DMFT and by standard DFT. Figure 1b reproduces measured in-plane optical conductivity from refs 11 and 12. Both theory and experiments11,12 show a reduction of the low-frequency Drude peak, which indicates a removal of a large fraction of carriers in the ordered state. Our calculation captures all the important qualitative features measured in experiments. In both PM and SDW states there is a broad peak due to interband transitions centred around 5,500 cm−1(ref. 13). Below 2,000 cm−1 the optical conductivity of the SDW phase shows a few extra excitations appearing as peaks and shoulders centred at 1,250 cm−1 (arrow 2 in cyan), shoulder structure at about 800 cm−1 (arrow 1 in blue) and a small peak at 1,800 cm−1 (arrow 3 in green). These extra excitations appear in experiment at slightly lower energies, as seen in Fig. 1a and b.

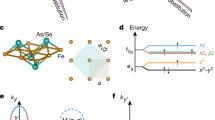
Figure 1: Optical conductivity and DOS of BaFe2As2 in the SDW and PM states.
figure 1

a, Calculated in-plane average optical conductivity. b, Experimental in-plane average optical conductivity. Data are taken from refs 11 and 12. c, The x x, y y and in-plane average optical conductivity in the SDW state. d, Total DOS. e, The projected DOS of Fe 3d x z, y z and x y orbitals in the SDW state calculated by DFT+DMFT, plotting positive (negative) for majority (minority) spin.

Full size image

These extra peaks and shoulders strongly depend on the polarization of light, as shown in Fig. 1c, where we plot separately the x and the y components of the optical conductivity. The first two excitations (blue arrow 1 and cyan arrow 2) are much more pronounced in the x direction, whereas the third peak (green arrow 3) is more pronounced in the y direction. The low-frequency optical conductivity is considerably larger in the x direction below 1,500 cm−1, whereas it becomes larger in the y direction above 1,500 cm−1. Around zero frequency, the optical conductivity of the SDW phase shows Drude-like behaviour, with Drude weight substantially smaller than in the PM phase. The theoretical value of the plasma frequencies ωp,x x, ωp,y y and ωp,z z in the x, y and z directions are 1.19, 0.95 and 0.76 eV, respectively, much smaller than the in-plane plasma frequency of 1.60 eV of DFT+DMFT calculation13 and experimental measurements11,14 in the PM state. The reduction of in-plane plasma frequency in the SDW state was also observed experimentally11. The estimated resistivity ratio along the y and x directions Ry/Rx≃ωp,x x2/ωp,y y2 is about 1.57, which agrees well with recent measurements by Chu et al. 4 and Tanatar and colleagues15. The anisotropy of the in-plane optical conductivity has not been studied experimentally, because of the fairly coarse spatial resolution imposed by the diffraction limit, spanning multiple magnetic domains. Near-field optics16, or techniques to prepare monodomain samples4, are promising avenues to test our prediction.

It is useful to analyse the optical conductivity at various frequency scales. The Drude weight is controlled by the Fermi-surface size, and by the mass enhancement of the low-energy quasiparticles. In the SDW state, the mass enhancement is smaller (2, 1.7, 1.7 and 1.5 for the t2g/majority, t2g/minority, e g/majority, e g/minority orbitals, respectively) than in the PM state (3 and 2 for the t2g and e g orbitals, respectively). Although the quasiparticles become lighter in the SDW phase, the Fermi-surface area is much smaller, and the latter effect dominates, resulting in a reduction of the Drude weight.

We also integrated the in-plane optical conductivity to obtain the effective kinetic energy of a low-energy model in both phases. At very low energies, the onset of magnetism results in an increase of the optical conductivity, because the SDW phase is more coherent than the correlated paramagnetic state. Consequently the very low-energy model gains kinetic energy in the ordered state. At intermediate energies, however, kinetic energy is lost as the result of the SDW gap opening on the Fermi surface.

As the optical conductivity of the PM phase is quite temperature dependent, we compare the SDW phase and PM phase at the same temperature (T=72.5 K), the latter being a metastable state at low temperature. Using this procedure, we find that the missing weight from opening the SDW gap is recovered only around 10,000 cm−1, a many times larger scale than the gap value. This should be contrasted with the classic weakly correlated materials, where the spectral weight is recovered immediately above the SDW gap.

We now turn to the electronic density of states (DOS). Figure 1d shows the total DOS in both the PM and SDW phases. In the SDW phase, the DFT+DMFT DOS shows a clear pseudogap on the energy scale of 0.15 eV around the Fermi level, in good agreement with scanning tunnelling microscopy measurements5. The LSDA DOS also shows a pseudogap at the Fermi level17; however, its width is more than 0.5 eV, therefore LSDA misses the structure below 4,000 cm−1 in the optical conductivity.

The onset of the SDW phase is also accompanied by a rearrangement of the iron crystal-field states, which gives rise to orbital polarization. This polarization is uniform in space (ferro-orbital polarization), as surmised by Singh18. The partial DOS of an Fe atom is shown in Fig. 1e. The minority density is given a negative sign. To extract the anisotropy of the electronic structure, we integrate the partial density of states of x z and y z orbitals (Ax z(ω) and Ay z(ω)) to obtain their occupations, and evaluate their difference . This defines the energy-dependent orbital polarization. For large cutoff Λ, the orbital polarization is close to zero for majority electrons and around 0.13 for minority electrons. At low energy, the anisotropy is enhanced to 1.23 (0.45) for majority (minority) carriers when Λ is 0.15 eV, the size of the optical SDW gap.

The optical conductivity in the x (y) direction comes primarily from excitations among x z (y z) and x y orbitals. The anisotropy of the partial DOS provides a natural explanation for the anisotropy of the optical conductivity; the y z density of states has fewer electronic states at the Fermi level and the main peak of the y z orbital is further away from the Fermi level compared with the x z orbital. We notice that only the low-energy orbital polarization is large, whereas the static orbital polarization (that is, the net imbalance between the static occupations of the x z and y z orbitals) is very small and unimportant for the anisotropy.

In Fig. 2a, we show DFT+DMFT momentum-resolved electronic spectra A(k,ω) in the SDW phase. This quantity is probed by angle-resolved photoemission spectroscopy (ARPES). Figure 2b,c compares the Fermi surface of the PM and SDW states, shown in the PM Brillouin zone.

Figure 2: ARPES and Fermi surface of BaFe2As2.
figure 2

a, A(k,ω) in the Γ plane in the path M′ΓMΓ of the SDW state. In the path MΓ we overlaid ARPES data from ref. 6. b, Fermi surface in the PM state. c, Fermi surface in the SDW state, plotted in the PM Brillouin zone. Blue arrows mark the position of the Dirac cones. d, A(k,ω) in the SDW state with shadow bands plotted by equal intensity for clarity. Arrows mark the three types of optical transition that give rise to the three peaks in the optical conductivity.

Full size image

In the PM state, the topology of the Fermi surface is very similar to DFT predictions19, with three cylinders centred at the Γ point and two at the M point. In the SDW phase, the Fermi surfaces of the LSDA calculation (not shown) and DFT+DMFT are very different. The magnetic order reconstructs the Fermi surface into smaller more three-dimensional pockets. Out of three cylinders centred at the Γ point, one remains in the SDW phase. This cylinder does not intersect the Γ plane within the LSDA (not shown), but has been clearly identified in experiment. The other cylinders reconstruct into more three-dimensional pockets.

In the SDW state, there are two inequivalent directions between Γ and M, here named M and M′, pointing along the antiferromagnetic and ferromagnetic directions of the Fe–Fe bonds, respectively (see Fig. 2b). Graphene-like Dirac points were recently identified by ARPES along the antiferromagnetic direction6. Figure 2a shows that a crossing of two bands occurs very near the Fermi level between Γ and M, at three-quarters of the distance, marked by a white arrow. The crossing is below the Fermi level, hence the pocket is electron-like. In Fig. 2c we mark the same tiny pocket by blue arrows, to show that it has indeed the shape of a Dirac cone. There are two such symmetry-related Dirac cones in the Γ plane and two in the Z plane. Notice that these cones appear only in the path from Γ to M (antiferromagnetic direction) and not in Γ to M′.

In the most right-hand part of Fig. 2a, we overlay our results with ARPES measurements of ref. 6, to emphasize common features. The overall position of the bands is in very good agreement without any need for a shift of the Fermi level or renormalization of the bandwidth, in contrast to the common need for shifts and renormalization when comparing DFT-derived bands with ARPES.

The DFT+DMFT Fermi surface also has good agreement with the ARPES measurement in the Z plane in ref. 20. In particular, the red electron pockets centred at Z, which have a two-fold symmetry and mostly x z character, were identified in ref. 20.

In Fig. 2d we replot the momentum-resolved electronic spectra A(k,ω) without the SDW coherence factors, to enhance the shadow bands. The arrows in this graph connect the features in the electronic structure with the peaks in the optical conductivity. We mark three types of vertical transition corresponding to the three peaks in Fig. 1. The first shoulder comes primarily from transitions within the x z orbital, namely between the flat band around −0.1 eV and the hole pocket at Γ and M. These transitions are between a shadow band and a non-shadow band, hence they appear only in the SDW phase. The second peak in optical conductivity, marked by a cyan arrow, comes primarily from transitions between the x z and x y orbitals, with some transitions between non-shadow bands only, visible also in the PM state, and some extra transitions between a shadow and non-shadow band. Finally, the third peak comes mostly from transitions between the x y and x y orbitals and the x y and y z orbitals, and mostly from transitions between a shadow and a non-shadow band.

In correlated materials, new physics, such as superconductivity, spin and orbital polarizations, emerges from the competition between Coulomb interaction and kinetic energy. A unique physical characteristic of iron arsenic materials is that the kinetic-energy loss in the SDW phase is compensated by a gain in Hund’s-rule coupling energy. Comparison of the SDW and PM histograms, describing the probabilities of different iron configurations in the solid, shows that in the SDW state the high-spin states become more probable. This results in an overall gain of the Hund’s-rule coupling energy of about 50 meV per Fe. Overall kinetic energy is lost in the SDW state at about 30 meV per Fe, resulting in a net energy gain of about 20 meV per Fe. This is different from the classical SDW transition, where kinetic energy is compensated by the reduction of the Hubbard correlations. Therefore, the nature of magnetism in iron pnictides is intermediate between the spin density wave of almost independent particles and the antiferromagnetic state of local moments.

The competition between kinetic and correlation energy takes different forms at different energy scales, and results in an unusual energy dependence of the spin and orbital polarizations. Spin polarization affects most strongly the electrons far below the Fermi level. For example, the exchange splitting—as determined from the frequency-dependent potential (self-energy) at high frequency—is three times larger than at zero frequency (see Supplementary Information). This high-frequency regime is governed by strong Hund’s-rule coupling on the iron atom, enhancing the magnetic moment.

At low energies, in the SDW state, well-defined quasiparticles form, and the residual Hund’s-rule coupling between these quasiparticles is weak. To minimize the kinetic-energy loss in the spatially anisotropic SDW phase, the quasiparticles propagate mainly along the antiferromagnetic x direction, hence the Drude peak is larger in the x direction than in the y direction. However, polarization is large only at low energy, where the quasiparticles are well formed, and the effective Hund’s-rule coupling is weakest (see Supplementary Information).

Our finding that spin polarization is larger at high energy whereas the orbital polarization is most pronounced at low energies leads to definite predictions for the anisotropy of the optical conductivity and can also be tested by scanning tunnelling microscopy.

The dichotomy of polarizations and the different characters (coherent versus incoherent) of the states close to and far from the Fermi surface is not captured by static mean-field theories. These methods can describe the physics in the low-energy range by adjusting one parameter but necessarily fail in the high-energy region. This was recently exemplified in ref. 21, where the static method DFT+U with negative U was used to bring the low-energy optical conductivity to better agreement with experiment than in standard DFT. To achieve this result with a static method, the magnetic moment, a high-energy quantity, has to be reduced to 0.3 μB, substantially below its experimental value, and the resulting higher-energy optical conductivity is not in good agreement with experiment. This failure of DFT is not connected to the proximity to a quantum critical point, but has to do with the well-known fact that, in correlated situations, static mean-field theories capture correlation effects by overemphasizing the ordering tendencies and can only be remedied by a correct treatment of dynamical effects.

In a renormalization-group picture of this material, we observe a different strength of the Hund’s-rule coupling at different energy scales. At high energy, Hund’s-rule coupling is very strong, whereas it fades away at low energy but gives an imprint on the massive and anisotropic low-energy quasiparticles. This is central for a proper description of the magnetic phase, and is likely to be important for the mechanism of the unconventional superconductivity in these materials.

Methods

To show that the origin of the in-plane anisotropy is electronic rather than structural, we use the experimental lattice constants and internal coordinates of the paramagnetic phase7. We use the continuous-time quantum Monte Carlo as the impurity solver in its spin-rotational invariant form, and the fully charge-self-consistent version of DFT+DMFT, described in detail in ref. 22. We use the ab initio-determined Coulomb interaction strength U=5.0 eV, the Hund’s coupling J=0.7 eV (ref. 13), and temperature T=72.5 K. To explore the sensitivity of the magnetic moment to the strength of the Coulomb interaction, we carried out calculations for other values of U and J around the ab initio values. We found that the size of the magnetic moment can be well parameterized by the simple formula m=(0.4 U+7.2 J−6.1 eV) μB eV−1 (see Supplementary Information). Hence, magnetization is most sensitive to the value of J, rather than U.