Abstract
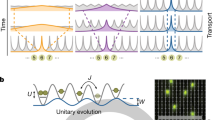
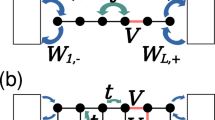
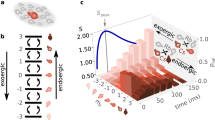
Quantum critical points are characterized by scale-invariant correlations and therefore by long-range entanglement. As such, they present fascinating examples of quantum states of matter and their study is an important theme in modern physics. However, little is known about the fate of quantum criticality under non-equilibrium conditions. Here we investigate the effect of external noise sources on quantum critical points. It is natural to expect that noise will have a similar effect to finite temperature, that is, destroying the subtle correlations underlying the quantum critical behaviour. Surprisingly, we find that the ubiquitous 1/f noise does preserve the critical correlations. The emergent states show an intriguing interplay of intrinsic quantum critical and external-noise-driven fluctuations. We illustrate this general phenomenon with specific examples describing solid-state and ultracold-atoms systems. Moreover, our approach shows that genuine quantum phase transitions can exist even under non-equilibrium conditions.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Winkler, K. et al. Coherent optical transfer of Feshbach molecules to a lower vibrational state. Phys. Rev. Lett 98, 043201 (2007).
Ni, K-K. et al. A high phase-space-density gas of polar molecules. Science 322, 231–235 (2008).
Blatt, R. & Wineland, D. J. Entangled states of trapped atomic ions. Nature 453, 1008–1015 (2008).
Lahaye, T., Menotti, C., Santos, L., Lewenstein, M. & Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 72, 126401 (2009).
Porras, D. & Cirac, J. I. Effective quantum spin systems with trapped ions. Phys. Rev. Lett. 92, 207901 (2004).
García-Mata, I., Zhirov, O. & Shepelyansky, D. Frenkel–Kontorova model with cold trapped ions. Eur. Phys. J. D 41, 325–330 (2007).
Deslauriers, L. et al. Scaling and suppression of anomalous heating in ion traps. Phys. Rev. Lett. 97, 103007 (2006).
Labaziewicz, J. et al. Temperature dependence of electric field noise above gold surfaces. Phys. Rev. Lett. 101, 180602 (2008).
Schmidt, A. Diffusion and localization in a dissipative quantum system. Phys. Rev. Lett. 51, 1506–1509 (1983).
Chakravarty, S. Quantum fluctuations in the tunneling between superconductors. Phys. Rev. Lett. 49, 681–684 (1982).
Leggett, A. J. et al. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 59, 1–85 (1987).
Clarke, J. & Wilhelm, F. K. Superconducting quantum bits. Nature 453, 1031–1042 (2008).
Ithier, G. et al. Decoherence in a superconducting quantum bit circuit. Phys. Rev. B 72, 134519 (2005).
Mitra, A., Takei, S., Kim, Y. B. & Millis, A. J. Nonequilibrium quantum criticality in open electronic systems. Phys. Rev. Lett. 97, 236808 (2006).
Diehl, S. et al. Quantum states and phases in driven open quantum systems with cold atoms. Nature Phys. 4, 878–883 (2008).
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, 1999).
Sondhi, S. L., Girvin, S. M., Carini, J. P. & Shahar, D. Continuous quantum phase transitions. Rev. Mod. Phys. 69, 315–333 (1997).
Giamarchi, T. Quantum Physics in One Dimension (Oxford Univ. Press, 2004).
Morigi, G. & Fishman, S. Eigenmodes and thermodynamics of a Coulomb chain in a harmonic potential. Phys. Rev. Lett. 93, 170602 (2004).
Antal, T., Rácz, Z. & Sasvári, L. Nonequilibrium steady state in a quantum system: One-dimensional transverse Ising model with energy current. Phys. Rev. Lett. 78, 167–170 (1997).
Feldman, D. E. Nonequilibrium quantum phase transition in itinerant electron systems. Phys. Rev. Lett. 95, 177201 (2005).
Zimmerli, G., Eiles, T. M., Kautz, R. L. & Martinis, J. M. Noise in the coulomb blockade electrometer. Appl. Phys. Lett. 61, 237–239 (1992).
Cladeira, A. O. & Leggett, A. J. Path integral approach to quantum Brownian motion. Physica A 121, 587–616 (1983).
Fisher, M. P. A. & Zwerger, W. Quantum Brownian motion in a periodic potential. Phys. Rev. B 32, 6190–6206 (1985).
Haldane, F. D. M. Effective harmonic-fluid approach to low-energy properties of one-dimensional quantum fluids. Phys. Rev. Lett. 47, 1840–1843 (1981).
Daley, A. J., Fedichev, P. O. & Zoller, P. Single-atom cooling by superfluid immersion: A nondestructive method for qubits. Phys. Rev. A 69, 022306 (2004).
Polkovnikov, A., Altman, E. & Demler, E. Interference between independent fluctuating condensates. Proc. Natl Acad. Sci. USA 103, 6125–6129 (2006).
Stenger, J. et al. Bragg spectroscopy of a Bose–Einstein condensate. Phys. Rev. Lett. 82, 4569–4573 (1999).
Steinhauer, J. et al. Bragg spectroscopy of the multibranch Bogoliubov spectrum of elongated Bose–Einstein condensates. Phys. Rev. Lett. 90, 060404 (2002).
Clément, D., Fabbri, N., Fallani, L., Fort, C. & Inguscio, M. Exploring correlated 1d Bose gases from the superfluid to the Mott-insulator state by inelastic light scattering. Phys. Rev. Lett. 102, 155301 (2009).
Kane, C. L. & Fisher, M. P. A. Transmission through barriers and resonant tunneling in an interacting one-dimensional electron gas. Phys. Rev. B 46, 15233–15262 (1992).
Kollath, C., Meyer, J. S. & Giamarchi, T. Dipolar bosons in a planar array of one-dimensional tubes. Phys. Rev. Lett. 100, 130403 (2008).
Refael, G., Demler, E., Oreg, Y. & Fisher, D. S. Superconductor-to-normal transitions in dissipative chains of mesoscopic grains and nanowires. Phys. Rev. B 75, 014522 (2007).
Kamenev, A. & Levchenko, A. Keldysh technique and non-linear sigma-model: Basic principles and applications. Adv. Phys. 58, 197–319 (2009).
Acknowledgements
We thank E. Berg, S. Huber, S. Kivelson, A. Lamacraft, K. Moler and E. Zeldov for stimulating discussions. This work was partially supported by the US–Israel BSF (E.A. and E.D.), ISF (E.A.) and Swiss SNF under MaNEP and division II (T.G.). E.D. acknowledges support from NSF DMR-0705472, CUA, DARPA-OLE and AFOSR-MURI. E.G.D.T. is supported by the Adams Fellowship Program of the Israel Academy of Sciences and Humanities.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 213 kb)
Rights and permissions
About this article
Cite this article
Dalla Torre, E., Demler, E., Giamarchi, T. et al. Quantum critical states and phase transitions in the presence of non-equilibrium noise. Nature Phys 6, 806–810 (2010). https://doi.org/10.1038/nphys1754
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1754
This article is cited by
-
Fokker-Planck equations for a trapped particle in a quantum-thermal Ohmic bath: general theory and applications to Josephson junctions
AAPPS Bulletin (2023)
-
Photonic materials in circuit quantum electrodynamics
Nature Physics (2020)
-
Incoherent quantum algorithm dynamics of an open system with near-term devices
Quantum Information Processing (2020)
-
Uhlmann curvature in dissipative phase transitions
Scientific Reports (2018)
-
Universal energy fluctuations in thermally isolated driven systems
Nature Physics (2011)