Elimination, reversal and directional bias of optical diffraction

Abstract

Any image, imprinted on a wave field and propagating in free space, undergoes a paraxial diffraction spreading. The reduction or manipulation of diffraction is desirable for many applications, such as imaging, wave-guiding, microlithography and optical data processing. As was recently demonstrated, arbitrary images imprinted on light pulses are dramatically slowed^1,2 when traversing an atomic medium of electromagnetically induced transparency^3,4 and undergo diffusion due to the thermal atomic motion^5,6. Here we experimentally demonstrate a new technique to eliminate the paraxial diffraction and the diffusion of slow light, regardless of its position and shape⁷. Unlike former suggestions for diffraction manipulation^8,9,10,11,12, our scheme is linear and operates in the wavevector space, eliminating the diffraction for arbitrary images throughout their propagation. By tuning the interaction, we further demonstrate acceleration of diffraction, biased diffraction and induced deflection, and reverse diffraction, implementing a negative-diffraction lens¹³. Alongside recent advances in slow-light amplification¹⁴ and image entanglement¹⁵, diffraction control opens various possibilities for classical and quantum image manipulation.

Main

Electromagnetically induced transparency (EIT) is a coherent two-photon interaction between light and atoms¹⁶. It involves an atomic medium and two light fields, usually a strong ‘pump’ and a weak ‘probe’, resonantly coupling two of the atomic levels to a common excited level. When the Raman resonance condition is satisfied, namely when the two-photon frequency detuning, Δ, is within the atomic spectral width, Γ, the atoms are driven towards a ‘dark’ state, which substantially reduces the absorption in the medium. A short probe pulse propagates in the medium with a reduced group velocity, owing to the steep dispersion inside the narrow transparency window^{4,17,18,19,20,21}. A travelling atomic-coherence field accompanies the probe, and the combined light–matter excitation is termed a dark-state polariton²². If an image is imprinted on the probe field in the plane normal to the propagation direction, the complex amplitude of the dark-state polariton follows the amplitude and phase of the image. Free-space diffraction, being essentially a geometric effect, occurs for slow images precisely as it would in free space.

In an EIT medium of hot vapour, the thermal motion of the atoms affects the propagation of images. The addition of a buffer gas attenuates the thermal motion, which becomes diffusive and can be characterized by a single diffusion coefficient, D. As a result, on EIT resonance, the atomic part of the dark-state polariton undergoes diffusion while propagating slowly in the medium⁵. The polariton thus experiences both diffraction and diffusion. Here, we exploit the atomic motion to influence the diffraction, as illustrated in Supplementary Fig. S1. Altering the Raman detuning provides control of the polariton’s coupling with atoms moving in a desired direction. We therefore counterbalance diffraction by ‘Doppler trapping’ the outwards-confronting light components with inwards-moving atoms or, alternatively, force diffraction in a preferable direction.

The free-space diffraction of an optical field envelope E(x,y;z) travelling in the z direction is described in the transverse Fourier plane (Fig. 1a) as , where is the transverse wavenumber, q=2π/λ and λ is the optical wavelength. In a vapour EIT medium, the propagation of a weak probe depends on its angular deviation from the pump due to the Doppler–Dicke effect^23,24. For a wide homogenous non-diverging pump, finite-pump effects such as transverse intensity variation²⁵ and Ramsey narrowing²⁶ are made negligible, and the dynamics of the probe becomes⁵ , where is the linear susceptibility and

Here, 2α is the absorption outside the EIT window, Γ_p is the power-broadening width, proportional to the pump intensity, and D k² is the Doppler–Dicke width. The latter has a simple physical interpretation: both the residual Doppler broadening and the Dicke narrowing are linear in k, which corresponds to the angle between the probe and pump, resulting in a combined quadratic effect²⁴. At a given Δ, different k components of a probe image experience different EIT spectra, and consequently the image is altered. When Δ=0 (red lines in Fig. 1b), χ_EIT is purely imaginary and induces a low-pass absorption filter in k space, with a half-width of . For k≪k₀, the filter is quadratic in k and corresponds to standard diffusion, accompanied by the free-space diffraction. To manipulate diffraction, a non-zero Raman detuning should be introduced. The case Δ=±Γ is of special importance: in this case, the leading quadratic term becomes purely real, inducing diffraction without diffusion,

with v_g=Γ²/(α Γ_p) being the slow group velocity. Here, the induced diffraction is continuous, in contrast to the diffraction manipulation explored in periodic systems^27,28,29. When Δ=−Γ the induced diffraction negates the free-space diffraction, and if v_g=D q they are cancelled altogether. As demonstrated in Fig. 1b (black lines), for k≪k₀, the susceptibility curves are flat and both diffraction and diffusion are eliminated. In contrast, when Δ=+Γ, the induced and the free-space diffraction add together, increasing the overall diffraction. Note that for given D and q the amount of induced diffraction is determined exclusively by the group velocity, which is easily controlled by the pump power and the atomic density. A major difficulty of the scheme is the substantial absorption at Δ≠0. Fortunately, this absorption is uniform both in real and k spaces and may be compensated for by any linear gain mechanism^7,14.

Figure 1: EIT susceptibility in k space and the experimental set-up.

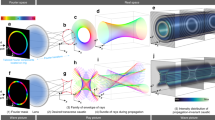
a, An image in the transverse plane, decomposed into its transverse-momentum components. The spectra as a function of k correspond to the experiments presented in (I) Fig. 2a and (II) Fig. 2b. b, The total susceptibility (solid lines): imaginary part (top), corresponding to diffusion, and real part (bottom), corresponding to diffraction. For Δ=−Γ, both curves are flat up to the fourth order in k. The dashed line shows the contribution from the EIT for Δ=−Γ, imposing negative diffraction at k≪k₀ and cancelling the free-space diffraction (k₀=20 mm⁻¹). c, The experimental set-up. An image is imprinted on the probe beam using a binary mask, and is imaged onto the entrance facet of the cell by a 4f imaging system. An iris in the central focus point acts as a low-pass filter for the image. The collimated pump and the probe, of orthogonal linear polarizations, are combined on a polarizing beam splitter (PBS), rotated to circular polarizations with a λ/4 plate, passed through the 50-mm-long ⁸⁷Rb cell, rotated back to linear polarizations and split using a second PBS. The probe is imaged from the exit facet of the cell onto a CCD (charge-coupled device) camera. Further details are given in Supplementary Information. d, The Λ-type level diagram depicts the part of the ⁸⁷Rb D1 line that was used in the experiment.

The experimental set-up is depicted in Fig. 1c. A glass vapour cell of length L=50 mm is air-heated to 72 ^∘C and filled with ⁸⁷Rb and 10 torr of neon buffer-gas. The rubidium diffusion coefficient is D=1,100 mm² s⁻¹, satisfying the diffraction-elimination condition with . For our optical depth (∼6), we arrive at these conditions with a pump intensity of 660 μW mm⁻², yielding an EIT line-width of Γ=70 kHz and transmission at Δ=±Γ of about 1%. In each shot, an image is imprinted on a weak probe pulse (2 μW mm⁻²) and projected onto the entrance facet of the cell. The transmitted probe at the exit facet is recorded with a CCD camera.

A demonstration of image propagation without diffraction is presented in Fig. 2a with an image of the symbol ‘®’. The 100-μm features in the image are significantly distorted after 50 mm of free-space diffraction. On the EIT resonance (Δ=0), the image covers this distance in 5.75 μs, during which it diffracts and diffuses. However, for Δ=−Γ, both diffraction and diffusion are clearly suppressed. The corresponding calculations verify that the observed minor spreading for Δ=−Γ is due to subdiffractive²⁹ and subdiffusive terms of fourth order in k. Indeed, the k spectrum of the image extends beyond the k≪k₀ region (k₀=20 mm⁻¹), as seen in Fig. 1a (Experiment I). For Δ=+Γ, and as predicted in equation (2), the image does not diffuse but rather undergoes substantial diffraction, of effectively twice the distance travelled. The presented calculations are done numerically by taking the Fourier transform of the two-dimensional incident field, multiplying by , and taking the inverse Fourier transform. This computation does not require the paraxial k≪k₀ approximation and is hereafter denoted as the numerical calculation.

Figure 2: Elimination of diffraction of arbitrary images.

a, Top left, an image of the symbol ‘® ’ at the entrance facet of the vapour cell. Middle row, the image at the exit facet of the 50 mm cell without EIT (left, taken at off-resonance) and with EIT (right), for Δ=−Γ, 0, and +Γ(Γ=70 kHz). The Δ=0 image shows both the regular free-space diffraction and the diffusion associated with the atomic motion. The Δ=−Γ image manifests the elimination of diffraction, as well as the absence of diffusion. The Δ=+Γ image shows no diffusion and twice the effect of free-space diffraction—the sum of the free-space and the EIT-induced diffraction. The graph above indicates the transmitted power as a function of Δ. Bottom row, numerical calculations of the effect for each case, given the initial condition of the incident image. The elimination of diffraction is insensitive to small changes in the experimental conditions—see Supplementary Fig. S3. b, The incident image is an array of lines (3.3 lp mm⁻¹), such that after 50 mm of free-space propagation () new lines appear in the dark centres between the original lines (a reciprocal grating at ∼1/4 Talbot distance, with L_T=230 mm). The cyan curves are transverse cross-sections. The elimination of diffraction for Δ=−Γ and the doubling of the diffraction for Δ=+Γ are clearly seen. In the Δ=+Γ image, the original grating almost vanishes, which is equivalent to a half Talbot distance. In the Δ=0 image, regular free-space diffraction occurs (quarter Talbot distance), accompanied by diffusion, which completely blurs the lines. The bottom graph shows the contrast of the original grating compared to the reciprocal grating, with +1 corresponding to the initial image and −1 to the existence of only the reciprocal grating (half Talbot distance). The contrast is well explained by an analytic analysis, which considers the k spectrum of the image with a single carrier and two sidebands at ±2π/a (the exact spectrum is shown in Fig. 1a, Experiment II). The analytic expression is given in Supplementary Equation S5.

A slow image of a line grating, shown in Fig. 2b, provides a quantitative measurement of the actual diffraction and diffusion. This image has the property that it reappears periodically after propagating a distance of L_T=2a²/λ, known as the Talbot self-imaging distance, where a is the grating period. At L_T/2, a reciprocal grating is created; the original lines disappear and new lines appear in the originally dark areas. In our experiment, the cell length was ∼L_T/4, at which the amplitudes of the original and reciprocal gratings are equal, resulting in a grating with a period of a/2.

The results for Δ=−Γ,0,+Γ are presented in Fig. 2b. Evidently, the image does not change for Δ=−Γ, and it is essential to note that, in contrast to a self-imaging effect, the image is maintained throughout its propagation. In the Δ=0 image, diffusion broadens the lines and erases the grating. For Δ=+Γ, we observe double diffraction, with the reciprocal grating dominating the original, in correspondence to L_T/2. To quantify the amount of diffraction, we measure the intensities at the positions of the original and reciprocal gratings, 〈I_o〉 and 〈I_n〉 respectively, and define the contrast C=(〈I_o〉−〈I_n〉)/(〈I_o〉+〈I_n〉), shown in Fig. 2b. C=1 (−1) at integer (half-integer) Talbot distances, and C=0 when the original and reciprocal gratings are comparable. The maximum value of C is obtained at Δ=−Γ and is about 0.85. Notice that C=0 also when the gratings are indistinguishable owing to diffusion, and quantitative indicators that separate the diffusion and diffraction effects are given in the Supplementary Information.

In addition to the magnitude of diffraction, we can use the atomic-motion mechanism to control the diffraction directionality. By setting a small angle θ_pump between the pump and the z axis, as illustrated in Fig. 3a, we superimpose a transverse phase grating, exp(i x q θ_pump), on the pump–probe interference⁵, replacing D k² in equation (1) with (see Supplementary Equation S8). For Δ=±Γ and θ_pump≪(k₀/q), a term proportional to , which inflicts a directional deflection on the probe, at an angle , is added to the dispersion in equation (2). Similarly to the walk-off phenomenon in birefringence crystals, the beam is deflected whereas the carrier wavevector stays parallel to the z axis (equal-phase surfaces maintain their original orientation). Hence, the beam keeps its original direction on exiting the cell.

Figure 3: Induced deflection (walk-off) of the probe beam.

a, The pump is set at an angle θ_pump relative to the z axis, and the angular deflection of the probe, θ_probe, is measured. The drawing illustrates the directions for Δ<0. For Δ>0, the probe deflects in the opposite direction. b, At the conditions for diffraction elimination (Δ=−Γ, v_g=D q) the probe follows the direction of the pump for q θ_pump≪k₀. The experimental error in determining θ_probe is ±0.02 mrad; the error in θ_pump is much smaller. Inset, An explanation of the diffraction elimination through the deflection effect. At these specific conditions, the probe beam ‘finds’ the pump and refracts in its direction, regardless of the probe’s original direction. Thus, all the transverse momentum components of an image refract into the same direction and traverse the cell together, maintaining their phase relation. On exiting the cell, each component returns to its original direction.

We have performed deflection experiments in the conditions for diffraction elimination, v_g=D q and Δ=−Γ. Figure 3b presents the measured θ_probe versus the applied θ_pump, showing that θ_probe=θ_pump as long as the paraxial approximation holds (q θ_pump≪k₀). This striking phenomenon, that the probe takes the direction of the pump while in the cell regardless of the incident angle, provides another explanation for the elimination of diffraction. As illustrated in Fig. 3b (inset), all diverging k components of a focused beam are made to propagate in the axial (pump) direction while maintaining their phase relation, thus detaining the diffractive divergence. Supporting measurements and an analytic derivation are given in Supplementary Information.

Diffraction vanishes when the induced diffraction, D/(2v_g), is equal in size and opposite in sign to the free-space diffraction, 1/(2q). However, if the induced diffraction is strengthened, for example by lowering the group velocity, the overall diffraction will become negative. Such a medium reverses the diffraction of slow images and can undo diffraction that has already taken place. As far as spatial diffraction is concerned, a medium with negative diffraction behaves similarly to a negative-refraction-index medium, within the limits of the paraxial approximation. The effective index is n_eff=(1−q D/v_g)⁻¹. When v_g=q D/2, n_eff=−1 and the overall diffraction becomes exactly the opposite of free-space diffraction.

A fascinating application of negative-index materials is an unusual lens¹³, demonstrated in Fig. 4. This slab-shaped lens of length L and n_eff=−1 focuses the radiation coming from any point source, located at a distance u<L, to a distance v behind the lens, where u+v=L. Parallel light rays, however, are not focused and continue in their original directions. Indeed, the images in the experiment are reconstructed by the lens regardless of the distance u.

Figure 4: A negative-diffraction lens.

a, An image of the digit ‘2’ is created at u=25 mm in front of the entrance facet of the vapour cell, of length L=50 mm, and the CCD is positioned to image the plane that is v=25 mm behind the exit facet. b, The image is significantly blurred under free-space diffraction of 100 mm. c,d, In the negative-diffraction conditions, the 50 mm EIT cell acts as a lens, and the image is made to reappear. To achieve these conditions, the pump power is set to about half the power required for the elimination of diffraction, so that Γ=30 kHz, the group delay is doubled and . Because the EIT line-width is decreased, the k filter is narrower (k₀=13 mm⁻¹), making our paraxial approximation less valid and the lens marginally adequate for the purpose. The imperfections in the reconstruction are due to the small k₀. When entering the cell, the beams refract at an angle opposite to the incident angle, and refract back on exiting, similarly to a negative-refraction-index lens. However, as opposed to the latter, the optical k vectors do not refract, and it is beam trajectories that are illustrated by the blue lines in the figure. The outcome is independent of the longitudinal position of the cell, as seen by the resemblance of c and d. Note that this lens is limited to and is therefore not applicable to the evanescent components of the image³⁰.

As a geometrical effect, paraxial diffraction is manifested through k dependence of the dispersion curve. The optimal approach to eliminate it is to superimpose dispersion with the same form and the opposite sign that is uniform in real space. An EIT vapour medium with a buffer gas and a uniform pump manifests these properties. The pump provides the anisotropy needed to single out the transverse wavevector, and Dicke narrowing accounts for the quadratic k dependence. The strength, frequency and orientation of the pump control the magnitude, sign and direction of the resulting diffraction. The possibilities may be further extended by introducing a non-uniform pump. The phase gradient of the pump then acts as a vector potential for the probe, in an effective Schrödinger dynamics of a charged particle. Currently, inherent loss limits the effectiveness of the scheme, for example in terms of resolution. Resolving this limitation by combining linear gain, probably by using more elaborate Raman processes, would clear the way to a vast variety of applications, in microscopy, lithography, switching and more.