Main

Using light to change the s-wave scattering length a in ultracold gases offers more flexibility than a magnetic Feshbach resonance because it is possible to apply an almost arbitrary spatial pattern of light using holographic masks. The light intensity can vary on a length scale of typically one optical wavelength and the pattern can also be varied rapidly in time. This could be used for a variety of applications, such as the simulation of the physics of black holes3,4, the controlled creation of solitons5, studies of the collapse of a Bose–Einstein condensate (BEC) in an unusual regime6 and the simulation of certain Hamiltonians in which the scattering length needs to be different at different sites of an optical lattice7,8. Moreover, if each lattice site contains exactly two atoms16 and a is varied only on every second lattice site, one could associate molecules at every second lattice site by ramping the magnetic field across the Feshbach resonance, thus producing a quantum state that resembles that of a supersolid. Another possible application for the manipulation of a with light exists in gases consisting of a mixture of different species or spin states. It would be desirable to tune the various scattering lengths in such systems independently, but for that purpose more control parameters than just the magnetic field are needed. Furthermore, if a spatially random light intensity pattern is applied, the scattering length would vary randomly with position, which might give rise to new quantum phases of the atomic gas.

A known scheme to manipulate a using light uses a photoassociation resonance, sometimes also called an optical Feshbach resonance. But so far, photoassociation resonances have rarely been used to tune a because they induce rapid loss of particles. The experiments in refs 12, 13 both demonstrated a change of in 87Rb, where abg is the background value of a. For these parameters, both experiments incurred losses characterized by a two-body rate coefficient K2 with an estimated value of ∼10−10 cm3 s−1. Typical densities of the order of 1014 cm−3 result in lifetimes of the order of 100 μs, which is too short for many applications. Alkaline earth atoms offer the possibility to use photoassociation on narrow intercombination lines, which results in smaller loss rates15. But this is not feasible in the large number of experiments with alkali atoms.

Here, we experimentally demonstrate that laser light can noticeably shift a magnetic Feshbach resonance in 87Rb and at the same time induce considerably smaller rates of particle loss than an optical Feshbach resonance. We study the magnetic field dependence of for a large detuning of the laser from a bound-to-bound resonance and find a change in similar to that reported for optical Feshbach resonances. Furthermore, we study the system for smaller detunings and observe an Autler–Townes doublet in the particle loss. Our results are in good agreement with a theoretical model.

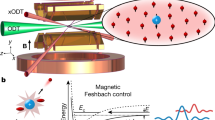
A basic level-scheme for our experiment is shown in Fig. 1. A light field is near-resonant with a bound-to-bound transition from the dimer state |g〉 in the electronic ground state to an electronically excited dimer state |e〉. In our system, the Feshbach resonance coupling between state |g〉 and the free-atom state |a〉 is much weaker than the bound-to-bound coupling due to the light field. In the limits of low density or high laser power this becomes true for arbitrary resonances, but for a very broad Feshbach resonance it might be difficult to reach this regime. Furthermore, we use one specific excited state |e〉 throughout this manuscript, for which the photoassociation coupling between states |a〉 and |e〉 is negligible. To understand the physics, it is useful to consider the energy eigenstates that are created from the two dimer states when applying the light. These eigenstates are superpositions of states |g〉 and |e〉 with corresponding energy shifts. The Feshbach resonance coupling probes the |g〉 components of both energy eigenstates, resulting in two resonances as a function of magnetic field B, in analogy to an Autler–Townes doublet17. Population in state |e〉 undergoes spontaneous radiative decay predominantly into other levels, not shown in Fig. 1. This leads to loss of population from the system. With all of the population initially in state |a〉, this loss can be described by a two-body loss rate coefficient K2.

Figure 1: Level scheme of the experiment.
figure 1

The Feshbach resonance couples atoms at the threshold in the incoming channel |a〉 to a bound dimer state |g〉 in a different potential. A laser is near-resonant with a bound-to-bound transition from |g〉 to an electronically excited dimer state |e〉.

Full size image

We use a mean-field approach to describe the population in each internal state. We assume that the bound-to-bound resonance and the spontaneous radiative decay both cause faster transitions than the Feshbach resonance coupling so that the population of the states |g〉 and |e〉 remains small and can be eliminated adiabatically from the equations of motion. This yields analytic results for the scattering length a and the loss rate coefficient K2. More details about the model are discussed in the Methods section. A very similar model was used in ref. 18 to explain an enhancement of photoassociation loss rates near a Feshbach resonance19,20. Our system differs from those references because we use levels where photoassociation is negligible.

The experimental procedure starts with a BEC of 87Rb atoms in the hyperfine state |F=1,mF=1〉 in an optical dipole trap with trap frequencies (ωx,ωy,ωz)/2π=(74,33,33) Hz. The magnetic field B is oriented along the z axis and held at a value that is a few gauss away from the Feshbach resonance at 1007.4 G (ref. 21). At time t=0, B is abruptly changed to a certain value at which it is held for 2 ms. The dipole trap is typically also switched off at t=0, except for in Fig. 2, where it is turned off at t=2 ms. During the 2 ms hold time of B, a travelling-wave laser beam is applied. This beam propagates along the vertical x direction, has a waist (1/e2 radius of intensity) of 0.17 mm and is π polarized; that is, its electric field oscillates along the z axis. The laser is beat-locked to a precision frequency comb and drives the bound-to-bound transition. After the 2 ms hold time of B, the laser and B are switched off simultaneously. This is followed by free flight and the atom cloud is imaged 18 ms after release from the dipole trap. The evolution of the cloud size during this sequence can be modelled in analogy to refs 22, 23. In addition, we include two-body loss in the corresponding equations of motion. This model is used to extract K2 and from the measured atom number and cloud size after expansion.

Figure 2: Shifting a Feshbach resonance with laser light.
figure 2

a, Real part of the scattering length as a function of magnetic field. In the absence of light (triangles), the pole in the scattering length occurs at 1007.4 G. With 4.2 mW of light applied, the Feshbach resonance is shifted to a different magnetic field. The data were recorded at a detuning of the light frequency with respect to the bound-to-bound resonance of ΔL/2π=+107 MHz (squares) and −107 MHz (circles). b, The application of the light induces two-body loss described by the rate coefficient K2 for a BEC. The observed loss when changing by ±1 is typically one order of magnitude lower than the loss that would be incurred when using an optical Feshbach resonance. Error bars represent one statistical standard error.

Full size image

The experimental data in Fig. 2 were recorded in a regime where the detuning of the light from the bound-to-bound resonance is much larger than the natural linewidth of state |e〉 and much larger than the energy width of the Feshbach resonance. In this regime, the light causes an a.c.-Stark shift of state |g〉, which results in a corresponding shift of the magnetic field at which the Feshbach resonance occurs. Figure 2a clearly shows this shift, which amounts to ∼±0.5 G.

Figure 2b shows the corresponding two-body loss rate coefficient K2 for a BEC. The solid lines are the predictions for K2 based on the model and parameter values presented in the Methods section. In the absence of light, K2 is zero. With the light on, we attribute all observed particle loss to K2. This overestimates K2 on the low-field side of the resonance, where part of the loss is actually caused by inelastic three-body collisions24. On the high-field side of the resonance, the three-body loss is less important23 and the extracted values for K2 for blue detuning (squares) agree well with the solid line. The agreement for red detuning (circles) is not quite as good.

To compare the results in Fig. 2 with an optical Feshbach resonance, we consider the data points in Fig. 2a with . For these data points, Fig. 2b shows K2∼10−11 cm3 s−1, which is an improvement by one order of magnitude compared with refs 12, 13.

Our technique offers two scenarios for applications. In the first scenario, the magnetic field can be held so close to the position of the unshifted Feshbach resonance, that this already changes a substantially. The light can then be used to shift the position of the Feshbach resonance in the magnetic field, thus bringing a back to abg in regions of high light intensity, whereas regions of low light intensity remain at a value far away from abg. In the second scenario, the magnetic field is held further away from the unshifted Feshbach resonance so that a∼abg. Application of the light can shift the Feshbach resonance so close to the chosen value of B that a is modified strongly in regions of high light intensity. In both scenarios, the light causes only a moderate shift of the Feshbach resonance; it does not need to induce a direct photoassociation coupling between the atomic and molecular state, which would result in loss just like for an optical Feshbach resonance.

Not all parameters of our model can be determined from the experiment discussed so far. To do this and to further explore the physics of our system, we study the regime of much smaller detuning of the laser light. In this regime, we clearly observe an Autler–Townes doublet as a function of B, as shown in Fig. 3. We fit the model from the Methods section to all of the data in this figure simultaneously. The fit agrees well with the experimental data.

Figure 3: Autler–Townes splitting of a magnetic Feshbach resonance caused by application of a laser that drives a bound-to-bound transition at a power of P=0.47 mW.
figure 3

a–e, The loss rate coefficient K2 is measured as a function of magnetic field B for different values of the laser frequency, which increase from a to e in steps of 1 MHz. Part c is recorded at 382,046,942.62 MHz, very close to resonance, where the Autler–Townes doublet becomes symmetric. The lines show a simultaneous fit to all of these data sets.

Full size image

We also recorded the position of the two loss resonances associated with the Autler–Townes doublet systematically as a function of laser frequency and laser power, as shown in Fig. 4. The data show typical features of an Autler–Townes doublet, namely an avoided level crossing in Fig. 4a and a splitting approximately proportional to the square root of the laser power in Fig. 4b. The data are well described by the model in the Methods section. We conclude that the relevant physics is well understood.

Figure 4: Systematic study of the resonance positions associated with the Autler–Townes doublet.
figure 4

a,b, The magnetic fields at which the loss resonances occur are shown as a function of laser frequency (a) and laser power (b). Part a was recorded at a power of 0.47 mW and clearly shows an avoided level crossing. Part b was recorded at a laser frequency of 382,046,943.00 MHz. The solid lines show the prediction of the model in the Methods section with the parameter values obtained from Fig. 3.

Full size image

The technique described here could be improved even further by using larger detuning combined with higher laser power, which should reduce the loss. Alternatively, the loss could be reduced by replacing the electronically excited dimer state |e〉 by a dimer state in the electronic ground state. The coupling to this state could be achieved with a stimulated two-photon Raman transition. Some potential applications of our method were already mentioned in the introduction. A further example is to shift one Feshbach resonance on top of another to explore the coupling between the two. Yet another possible application can be found in 133Cs. Its hyperfine state |F=3,mF=3〉 has a very broad Feshbach resonance at a slightly negative magnetic field. Applications of this Feshbach resonance are hampered by rapid loss due to dipolar relaxation at negative magnetic field. Shifting this Feshbach resonance to a positive magnetic field would make it accessible for experiments, such as studies of Efimov physics25.

Methods

A theoretical model for the experiment can be developed as follows. We denote the atomic state as |a〉, the dimer ground state as |g〉 and the electronically excited dimer state as |e〉. We describe the populations of the states with the mean fields ψa, ψg and ψe. Generalizing ref. 26, we use the following equations (similar to ref. 18)

Ubg=4πℏ2abg/m describes the atomic mean-field energy far away from the Feshbach resonance, where m is the mass of one atom and ℏ is the reduced Planck constant. The electric field of the light is E=−E0cos(ωLt) with amplitude E0 and angular frequency ωL. This field causes a coupling on the bound-to-bound transition . This coupling is treated in an interaction picture with a rotating wave approximation. The corresponding Rabi frequency is ΩR=degE0/ℏ, where deg=〈e|d|g〉 is the matrix element of the electric dipole moment. γe describes spontaneous radiative decay of state |e〉 into other states, which are not included in the model. Collisional decay is neglected.

The internal energy of each state depends nonlinearly on the magnetic field B. Near the pole of the unshifted Feshbach resonance Bpole we approximate this dependence as linear and obtain the internal energies Ejint=−μj(B−Bpole)+ℏωegδe j for j∈{a,g,e} with the magnetic moments μj and the Kronecker symbol δi j. At the Feshbach resonance (B=Bpole), states |a〉 and |g〉 are degenerate, whereas state |e〉 is offset by an energy ℏωeg. The internal energies are represented in an interaction picture that makes Eaint vanish and yields Δg=μa g(B−Bpole)/ℏ and Δe=−ΔL+μae(B−Bpole)/ℏ with μa g=2μa−μg, μae=2μa−μe and ΔL=ωL−ωeg.

The parameter α with |α|2=Ubgμa gΔB/2ℏ2 describes the Feshbach resonance coupling between states |a〉 and |g〉, where ΔB is the width of the Feshbach resonance. The parameter β∝E0 describes photoassociation from state |a〉 to |e〉, which turns out to be negligible for the parameters of our experiment.

We assume that states |g〉 and |e〉 never obtain a large population because α ψa and β ψa are both small compared with γe and ΩR. Hence, we can adiabatically eliminate states |g〉 and |e〉 and obtain a complex-valued scattering length in analogy to ref. 27

The two-body loss rate coefficient for a BEC is K2=−8πℏIm(a)/m. The Feshbach resonance used in our experiment has the following parameters23,28,29: Bpole=1007.4 G, abg=100.5a0, μa/2πℏ=1.02 MHz G−1, μa g/2πℏ=3.8 MHz G−1 and ΔB=0.21 G. A fit to the data in Fig. 3 yields the following best-fit values for the parameters of the bound-to-bound transition: ωeg/2π=382,046,942.8±0.3 MHz, |deg|/e a0=0.28±0.05, γe/2π=4.7±0.5 MHz, μae/2πℏ=2.6±0.1 MHz G−1 and a negligible result for β. Here, a0=52.92 pm is the Bohr radius and e=1.602×10−19 C is the elementary charge. The lines in Fig. 4b are plotted for |deg|/e a0=0.31. We attribute the deviation from the previous value of deg to a technical problem with the light intensity calibration. The excited state used here is a specific hyperfine and magnetic substate of the vibrational state v=120 in the attractive 1g potential that is adiabatically connected to the 2P3/2+2S1/2 threshold (C.-C. Tsai and D. Heinzen, personal communication).