Main

Trimer states arise as a natural consequence of two-body binding forces, but the general understanding of a quantum system of three interacting particles is a remarkably difficult task. For resonant two-body interactions, however, the energy spectrum follows simple, yet surprising rules, as manifested in Efimov’s scenario describing a series of trimer states4. Systems in nuclear physics5 and molecular physics11,12 were considered as candidates for Efimov states, but only recently ultracold atomic gases have opened up the possibility to realize and explore the required interaction conditions in a controlled way1,3. In view of these new developments, a particularly important question is how idealized few-body scenarios are connected to near-universal systems existing in the real world.

A universal three-body system of identical bosons can be fully characterized by two parameters, the two-body scattering length a and an extra three-body parameter; the latter results from short-range physics2. In principle, knowledge on one Efimov trimer state, for example its binding energy for a given value of a, is sufficient to determine the three-body parameter and thus to predict the complete spectrum. A test of universality in a real three-body system is possible, when at least two different pieces of information on the trimer spectrum become experimentally available. For the caesium system, information was obtained by measuring three-body recombination 1. The observation of a triatomic resonance marked the particular value of the negative scattering length where a trimer state of Borromean character5 reaches the threshold for dissociation into three free atoms. Observations at positive scattering lengths revealed a decay minimum, but an interpretation in terms of universal arguments is questionable because of ambiguities concerning the origin of this feature13.

Here, we follow a new experimental approach and show that an atom–dimer mixture provides experimental access to the situation where a non-Borromean trimer state couples to the threshold for dissociation into a free atom and a dimer. The phenomenon that we observe is a resonance in atom–dimer scattering, which manifests itself in resonantly enhanced inelastic decay. The resonance location provides an unambiguous piece of information that complements the previous results on caesium and facilitates a comparison with universal predictions concerning the spectrum of trimer states.

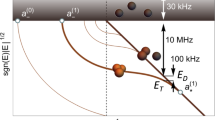
For caesium atoms in the lowest internal state (hyperfine and projection quantum numbers F=3 and mF=3), the s-wave scattering length a shows a pronounced dependence on the magnetic field in the low-field region below 50 G (see Fig. 1, inset). Over a wide range, |a| is very large and exceeds the range of the attractive van der Waals potential, which can be characterized3 by a length rvdW≃100 a0, where a0 is Bohr’s radius, and a corresponding energy EvdW≃h×2.7 MHz. Universality in general requires scattering lengths much larger than rvdW and energies much smaller than EvdW. For caesium, a near-universal halo dimer state 5,6,7 exists for large positive a with a binding energy of Eb=ℏ/(m a2)≪EvdW, where m is the atomic mass.

Figure 1: Three-body spectrum of caesium.
figure 1

The energies E of the atom–dimer thresholds (blue solid curves) are shown as a function of the magnetic field B. The red dashed lines illustrate Efimov-like trimer states, which are labelled by n′ and n on the left- and right-hand side of the zero crossing of the scattering length at 17 G, respectively. For the trimer states, the energy dependence is not precisely known. The giant three-body loss resonance found at 7.5 G (ref. 1) has pinpointed the intersection of an Efimov state with the three-atom threshold (open arrow). The intersection of an Efimov state with an atom–dimer threshold (filled arrow) leads to a resonance in atom–dimer relaxation. Zero energy corresponds to three atoms in the lowest spin state, labelled by the total spin quantum number F=3 and its projection mF=3. The inset shows the scattering length a as a function of the magnetic field B. The grey areas represent the non-universal regions, where |a|<rvdW=100 a0 or Eb>EvdW=h×2.7 MHz.

Full size image

A schematic diagram of the relevant three-body energy spectrum is shown in Fig. 1, illustrating the energies of trimer states (red dashed curves) and atom–dimer thresholds (blue solid curves). The energy dependencies of the thresholds are well known, because of the precise knowledge of the caesium two-body spectrum14. The dimer state that corresponds to the atom–dimer threshold at positive magnetic fields has near-universal halo character in a wide magnetic-field range above 20 G (ref. 7). The trimer states are located in the regime where |a| exceeds rvdW, with binding energies well below EvdW. We therefore refer to them as Efimov states 4, although sometimes more strict definitions are used15. An Efimov trimer intersects the three-atom threshold, at which three free atoms couple resonantly to a trimer. Similarly, an Efimov trimer couples to a halo dimer and a free atom at the atom–dimer threshold.

The energy spectrum of trimer states is not precisely known, but their appearance at the thresholds can give clear signatures of their locations. The observation of a giant three-body recombination loss resonance in an ultracold atomic caesium sample at 7.5 G, corresponding to a=−850 a0, has pinpointed the location at which one of the Efimov states (labelled n′=0) hits the three-atom threshold1 (open arrow in Fig. 1). The next Efimov resonance in three-body recombination loss (as caused by the state with n′=1) is predicted at negative magnetic fields, in principle accessible with atoms in the F=3, mF=−3 state. Unfortunately, in practice, its observation will be obscured by fast two-body losses3. Several studies have suggested the intersection of a trimer state with the atom–dimer threshold for positive magnetic fields below 50 G (T. Köhler, private communication, 2006; B. D. Esry, private communication, 2007; ref. 16; see filled arrow in Fig. 1). Note that in our case, the regions with a<0 and a>0 are connected through a zero crossing and not through a pole. Therefore, the states with n=1 and n′=1 are not adiabatically connected as they would in a complete realization of Efimov’s scenario.

The appearance of an Efimov trimer at the atom–dimer threshold is predicted to manifest itself in a resonant enhancement of atom–dimer relaxation9,10. Relaxation is energetically possible because of the presence of deeply bound dimer states and leads to loss of both the atom and the dimer from the trap, as the corresponding release of energy generally exceeds the trap depth. The resonant coupling of an atom and a dimer to a trimer opens up strong loss channels as the trimer state decays rapidly into a deeply bound dimer state plus a free atom. The particle loss is described by the rate equation , where nD(nA) is the molecular (atomic) density and β denotes the loss rate coefficient for atom–dimer relaxation. In the non-universal regime, relaxation loss in ultracold atom–dimer samples has been studied in various systems17,18,19,20 and was found to be essentially independent of the magnetic field. In the universal regime, suppression of loss has been observed in systems involving fermions21.

The experimental realization of an ultracold sample of simultaneously trapped atoms and dimers is a challenging task and requires special trap conditions (see the Methods section). We prepare an ultracold atomic sample in a crossed-beam optical dipole trap, after which a part of the atomic ensemble is converted into dimers by means of Feshbach association6,22 using a 200-mG-wide Feshbach resonance at 48 G (refs 7, 14). For our lowest temperatures of 30 nK, we obtain a mixture of about 3×104 atoms and 4×103 dimers. After preparation of the mixture, we ramp to a certain magnetic field and wait for a variable storage time. Then we switch off the trap and let the sample expand before ramping back the magnetic field over the 48 G resonance to dissociate the molecules, after which standard absorption imaging is carried out. During the expansion, a magnetic field gradient is applied to spatially separate the atomic and molecular cloud (Stern–Gerlach separation)22. In this way, we simultaneously monitor the number of remaining atoms and dimers (see Fig. 2a). A typical loss measurement is shown in Fig. 2b. We observe loss of dimers on a timescale of a few tens of milliseconds. To obtain β, we have set up a dimer loss model based on the above-mentioned rate equation (see the Methods section). Because the number of atoms greatly exceeds the number of dimers, a simple analytic expression can be derived, which is fitted to the data. The loss of dimers due to dimer–dimer relaxation is small and is taken into account; the corresponding loss rate for this process was measured independently using a pure dimer sample7.

Figure 2: Measuring the atom–dimer relaxation loss rate.
figure 2

a, Absorption image of the atom–dimer mixture after release from the trap and Stern–Gerlach separation. b, Time evolution of the number of atoms and dimers at 35 G. Here, the loss of dimers can be fitted with an exponential decay curve with a 1/e lifetime proportional to β−1, as the atom number greatly exceeds the dimer number and loss due to the dimer–dimer relaxation can be neglected (see the Methods section).

Full size image

The relaxation rate coefficient β is shown in Fig. 3 as a function of the two-body scattering length a; the inset shows the same data as a function of the magnetic field. For a<0 (B<17 G), we observe an essentially constant β of about 1.5×10−11 cm3 s−1. In this region, the atom–dimer system is non-universal and its properties are not directly related to the scattering length. With increasing a, β exhibits a strikingly different behaviour. We first observe a sharp rise in β, which reaches its maximum value at about a=400 a0 (B=25 G), and a subsequent smooth decrease towards values similar to those in the non-universal region. We interpret the observed resonant enhancement as being caused by the appearance of a three-body bound state at the atom–dimer threshold. Owing to the presence of the near-threshold trimer state, the atom–dimer scattering length is expected to diverge2. In analogy with a usual two-body Feshbach resonance, such a three-body resonance could offer the unique possibility to tune the atom–dimer interaction from attractive to repulsive while the atomic two-body scattering length a stays always positive.

Figure 3: Loss resonance in atom–dimer relaxation.
figure 3

The loss rate coefficient β for atom–dimer relaxation is shown as a function of the scattering length a (main figure) and the magnetic field B (inset); measurements are taken at temperatures of 40(10) nK (blue open triangles) and 170(20) nK (red closed squares). The error bars on β contain all statistical uncertainties (one standard deviation) from the fit of the time evolution as well as the trap frequencies and the temperature measurements (see the Methods section). The solid curve is a fit of an analytic model from effective field theory (see text) to the data for a>rvdW=100 a0.

Full size image

An intriguing question is whether the observed resonance is related to a trimer state that crosses the atom–dimer threshold or emerges from it. The behaviour of the relaxation rate with temperature can provide further insight on this subject. For crossing states, the trimers also exist in quasi-bound states in the continuum above the atom–dimer threshold, and the location of the loss maximum will show a related shift with temperature. For a trimer state merging with the threshold, such a shift will not occur. Efimov’s scenario predicts that in the Borromean region an Efimov trimer crosses the three-atom threshold, and measurements on the triatomic resonance position have indeed revealed a shift with temperature23. In contrast, for the non-Borromean region an Efimov trimer is expected to merge with the atom–dimer threshold, as illustrated in Fig. 1. Figure 3 shows two data sets at different temperatures, namely at 40(10) nK (blue open triangles) and 170(20) nK (red closed squares). We observe β to be independent of the temperature of the mixture. We do not observe any shift of the resonance position, supporting the expectation from Efimov’s scenario that the trimer state exists only below the atom–dimer threshold. In addition, also the magnitude of the loss rate is not affected by the temperature change, indicating that the measurements are in the threshold regime and not unitarity limited.

At large scattering length, trimer states are expected to have Efimovian character. In the non-Borromean region, Efimov physics manifests itself as a series of asymmetric resonances in the atom–dimer relaxation rate, in the universal limit separated by the factor eπ/s0≈22.7, where s0=1.00624. In the zero-temperature universal limit, an analytic expression of β has been found within an effective field theory10. The loss rate coefficient has the form β=CAD(a)ℏa/m with CAD(a)=D[sinh(2η*)/(sin2[s0ln(a/a*)]+sinh2η*)]. The parameters a* and η*, corresponding to the resonance position and the decay parameter respectively, are both free in the theory because the short-range physics of realistic three-body system is usually largely unknown. We compare our findings with the universal predictions by fitting the analytic expression of β to our 170 nK data in the region where a>rvdW=100a0, with a*, η* and D as free parameters. As shown in Fig. 3, we observe a good qualitative agreement, in particular regarding the characteristic shape of the observed loss feature. From the fit, we obtain a*=367(13) a0, η*=0.30(4) and D=2.0(2). In ref. 10, D is a fixed value, which is predicted to be 20.3 in the zero-temperature universal limit.

In the ideal Efimov scenario, the locations of the resonance features in atom–dimer relaxation at a*(n)>0 and those in three-body recombination at a−(n′)<0 are connected through the relation a*(n)/|a−(n′)|≈1.06×22.7(n−n′−1) (refs 2, 24). With the observation of a−(0)=−850(20) a0 (ref. 1) and our present finding of a*(1)=367(13) a0, we obtain a*(1)/|a−(0)|=0.43(2), which is significantly smaller than the value 1.06 in the ideal scenario. Theoretical models that take the finite range of the two-body potential into account13,25,26,27 have shown that finite-range corrections, which are particularly important for low-lying Efimov states, lead to shifts of the resonance positions. A downshift of a*(n) is expected along with an upshift of |a−(n′)|. This would indeed result in a smaller a*(1)/|a−(0)|. An alternative explanation would be a change in the three-body parameter between the a<0 and a>0 regions, which may occur in our case, where these regions are connected through a zero crossing instead of a pole in a.

We have observed a strong loss resonance in an ultracold atom–dimer mixture, induced by a weakly bound trimer state. Our work demonstrates that atom–dimer relaxation measurements can provide information on the three-body spectrum in a complementary way to three-body atomic recombination. To resolve the open issues regarding the relation between different resonance features, more efforts, both experimentally and theoretically, are necessary. On the experimental side, the realization of the complete Efimov scenario requires a Feshbach resonance in which both sides of the resonance are accessible. For caesium, a broad Feshbach resonance at 800 G is an excellent candidate for this purpose15. A full understanding of the three-body sector in real-world systems near universality is required as a prerequisite to explore more complex few-body phenomena2,28,29,30, such as the four-body scenario on which present experiments are beginning to shed new light7,30.

Methods

Preparation.

Our ultracold atom–dimer mixture is trapped in a crossed-beam optical dipole trap generated by two 1,064 nm laser beams with waists of about 250 and 36 μm (ref. 7). As atoms and dimers in general have different magnetic moments, the application of a levitation field is not appropriate and a sufficiently high optical gradient in the vertical direction to hold the atoms and dimers against gravity is required. However, to obtain very low temperatures and not too high densities, a tight trap is not advantageous. Here, we use an adjustable elliptic trap potential with weak horizontal confinement and tight confinement in the vertical direction. The ellipticity is introduced by a rapid spatial oscillation of the 36 μm waist beam in the horizontal plane with the use of an acousto-optic modulator, creating a time-averaged optical potential. The final temperature of the atomic and molecular sample can be set by varying the ellipticity and the laser power of the laser beam in the final trap configuration, and is in the range of 30–250 nK. For the lowest temperature samples, the final time-averaged elliptic potential is characterized by trap frequencies of 10 and 20 Hz in the horizontal plane, and 80 Hz in the vertical direction.

Dimer loss model.

We measure the atom–dimer relaxation loss rate β by recording the time evolution of the dimer number ND and atom number NA. In a harmonic trap, the atomic and molecular samples can be described by Gaussian density distributions, where the width depends on the trap frequencies, the temperature and the mass. Because the polarizability of the halo dimers is twice that of the atoms, the trap frequencies of the atoms and the dimers are the same. We find that the atomic and molecular samples have the same temperature7. The time evolution of ND can then be described by the following rate equation:

with and being the mean atomic and molecular density, respectively, m the atomic mass, the geometric mean of the trap frequencies and T the temperature. Here, loss of dimers due to dimer–dimer relaxation is also taken into account through the dimer–dimer relaxation loss rate coefficient α. Because of the unequal mass, the density distributions of the atomic and molecular samples are not the same. As a result, an effective atomic density experienced by the molecular cloud has to be considered, which is taken into account by the factor in front of the atom–dimer loss term18.

Our experiments are carried out in the regime in which NA≫ND and loss of atoms as a result of atom–dimer relaxation is negligible. Three-body recombination leads to atom loss on a much longer timescale compared with the molecular lifetime. Therefore, NA can be taken as a constant and equation (1) has the following solution:

where ND,0≡ND(t=0), and . If β NA≫α ND, that is, dimer–dimer relaxation loss is negligible compared with atom–dimer relaxation loss, equation (2) simplifies to

and ND shows an exponential decay with a 1/e lifetime of (b NA)−1. In our experiments, dimer–dimer relaxation loss can be neglected for B>20 G and equation (3) is fitted to the data. For B<20 G, β is much smaller than α (ref. 7) and the application of equation (2) is required, taking α from independent loss measurements of a pure dimer sample (ref. 7). For each measurement of β, the trap frequencies and the temperature are determined by sloshing mode and time-of-flight measurements, respectively.