Main

The hallmark of the Kondo effect in a quantum dot is an increase of the conductance below TK up to the unitary conductance 2e2/h at very low temperature and bias voltage. This corresponds to the opening of a spin-degenerate conducting channel of unit transmission at the Fermi energy of the electrodes, if only a single spin 1/2 is involved. The non-interacting theory of shot noise predicts no noise for such a quantum scatterer, as a consequence of Fermi statistics11. Does such a statement apply to a generic Kondo resonance?

In this letter, we show that, in contrast to the prediction of the non-interacting theory, a conductor in the Kondo regime can be noisy even though its conductance is very close to 2e2/h. We report on noise measurements carried out in single-wall-carbon-nanotube- (SWNT-) based quantum dots in the Kondo regime. We find an enhancement by up to an order of magnitude with respect to the non-interacting (Fermi-gas) theory of the shot noise within the Kondo resonance due to charge quantization combined with spin and orbital degeneracy. We can account for this enhancement with a fully interacting theory based on the slave-boson mean-field (SBMF) technique. We also find a non-monotonic variation of the equilibrium current fluctuations as the temperature is decreased below TK. Finally, the conductance and the noise obey a scaling law, the Kondo temperature kBTK being the only energy scale.

SWNTs are ideally suited to explore the noise in the Kondo regime of a quantum dot. They can show Kondo temperatures up to 10–15 K, which enables us to apply fairly high currents, up to 10 nA, within the Kondo resonance. This contrasts with semiconducting quantum dots, where Kondo temperatures are usually much smaller and therefore shot-noise measurements more difficult (a specific aspect of the spin-1/2 case could be studied only very recently in a lateral quantum dot12). In addition, carbon nanotubes make it possible to investigate a large class of different Kondo effects, including the simplest spin-1/2 Kondo effect5, the two-particle Kondo effect13, the orbital Kondo effect14 and the so-called SU(4) Kondo effect14,15.

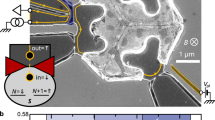
We first present results for device A, which consists of a SWNT contacted by two Pd electrodes separated by 200 nm (see Fig. 1b). Our measurement set-up, shown in Fig. 1b, enables us to measure simultaneously the noise and the conductance. The total current noise SI of the SWNT is obtained by subtracting a calibrated offset from the measured cross-correlations (see the Methods section and Supplementary Information). The colour-scale plot of the differential conductance of the sample is shown in Fig. 1a; the characteristic Kondo ridges are observed at 1.4 K as the horizontal lines within the Coulomb diamonds. We now study the two ridges, Sample A Ridge 1 (SAR1) and Sample A Ridge 2 (SAR2), corresponding to VG=11.26 V and VG=11.80 V respectively, indicated by arrows in Fig. 1a.

Figure 1: Anomalous temperature dependence of the current noise at the onset of the Kondo effect.
figure 1

a, Colour-scale plot of the differential conductance as a function of the gate voltage VG and the source–drain bias Vsd at temperature T=1.4 K. The characteristic horizontal lines in the middle of the Coulomb diamonds signalling the Kondo effect are observed. Orange lines, the linear conductance curves at T=1.4 K (solid line) and T=12 K (dashed line). b, Simplified diagram of the noise-measurement scheme and scanning electron microscope picture of a typical sample. The bar corresponds to 1 μm. c, Left, the non-monotonic temperature dependence of the equilibrium current fluctuations on the Kondo ridge SAR1 (VG=11.26 V (black squares)). Blue circles, the corresponding variation of G(T,Vsd=0). Solid black line, the dependence of SI predicted from the Johnson–Nyquist formula. Right, SI versus 4kBT G(T,Vsd=0). The line corresponds to the expected slope of unity. The error bars correspond to the mean square root of the statistical error and the systematic error due to fluctuations of the background.

Full size image

Signatures of the Kondo effect are already present in the equilibrium current fluctuations. From the fluctuation-dissipation theorem, the power spectral density of current noise is expected to be given by the Johnson–Nyquist formula: SI(Vsd=0)=4kBT G(T,Vsd=0), where G(T,Vsd)=dI/dV is the differential conductance at temperature T and source–drain bias Vsd. However, owing to Kondo correlations, G(T,Vsd=0) shows a sharp increase as T is lowered, as shown in Fig. 1c left in blue dashed lines. From the Johnson–Nyquist formula, an increase of G(T,Vsd=0) tends to produce an increase of SI as the temperature is lowered, but at zero temperature SI should be zero. Therefore, an unusual maximum can occur in the variation of SI as a function of temperature for a quantum dot in the Kondo regime. We observe such a maximum around 3 K for ridge SAR1, as shown in the left panel of Fig. 1c in black squares, which reaches about 7–9×10−27 A2 Hz−1 here. As expected, the Johnson–Nyquist relationship still holds, as shown in the right panel of Fig. 1c.

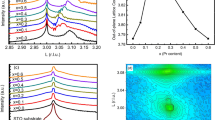
The bias dependence of G(1.4 K,Vsd) for SAR1 and SAR2 is shown in Fig. 2. The characteristic zero-bias peak of the Kondo effect is observed. The conductance at zero bias is, for both cases, close to 2e2/h (respectively 0.997×2e2/h and 0.865×2e2/h). The half-width of these resonances, of about 0.2 meV, gives an estimate of the Kondo temperature, of about 2.5 K, consistent with the temperature dependence shown in Fig. 1c (left). As shown in Fig. 2a,b (black squares), when a finite bias is applied, the total noise power spectral density SI increases from about 5×10−27 to about 8×10−27 A2 Hz−1 (7×10−27 A2 Hz−1) for SAR1 (SAR2) respectively. The ratio of SI to the Schottky value 2e Isd, where Isd is the current flowing through the nanotube at Vsd=0.84 mV, is about 0.84±0.09(0.89±0.1) for SAR1 (SAR2) respectively. Therefore, the noise remains sub-Poissonian.

Figure 2: Noise enhancement within the Kondo resonance.
figure 2

a, Conductance and noise measurements (black circles and black squares respectively) for Kondo Ridge 1 of Sample A (VG=11.26 V) at 1.4 K. The results of the SBMF theory, in solid red lines, are in good agreement with the conductance and the noise. b, Similar plots as in a for Kondo Ridge 2 of Sample A (VG=11.80 V). The Kondo resonance corresponds to a slightly different Kondo temperature. In both panels, the non-interacting theory, in blue dashed lines, does not account either for the conductance or for the noise. The error bars correspond to the mean square root of the statistical error and the systematic error due to fluctuations of the background.

Full size image

In general, the noise properties of carbon nanotubes are affected by the existence of a possible orbital degeneracy, which arises from the band structure of graphene, as recently shown in the non-interacting limit16. Therefore, a first step towards the understanding of the measurements presented in Fig. 2 is to use a resonant tunnelling model with two spin-degenerate channels, with transmission , di being the transmission of the channel of index i∈{1,2}, Γ being the width of the resonant level and ε being the energy. From the non-interacting scattering theory 11, the current and the noise associated with read

with fL=f(e Vsd/2+ε) and fR=f(−e Vsd/2+ε), f(ε) being the Fermi function at temperature T. The fits of dI/dV using equation (1) and , shown in blue dashed lines in Fig. 2a,b, yield d1=d2=0.95 (d1=d2=0.99) and Γ=0.11 meV (Γ=0.09 meV) respectively. These fits are poor because the Lorentzian line shape with constant Γ assumed for is not able to account for both the height and the width of the measured dependence of dI/dV as a function of Vsd. Furthermore, the noise variation obtained with formula (2) using the above values for d1, d2 and Γ, in blue dashed lines in the lower panels of Fig. 2a,b, is about an order of magnitude smaller than our experimental findings. Therefore, a simple non-interacting resonant-tunnelling theory cannot account either for the conductance or for the noise that we observe.

In the Kondo regime, in the case of a fourfold degeneracy and single charge occupancy, the maximum of the Kondo resonance lies at TK above the Fermi energy of the leads according to the Friedel sum rule, as depicted in Fig. 3b. From this, we can infer that, if the couplings of the level to the left ΓL and the right ΓR electrodes are the same (hereafter called the symmetric case), the differential conductance which saturates at 2e2/h corresponds to two channels of transmission 1/2 ((1/2)(4ΓLΓR/(ΓL+ΓR)2) in the general case). This corresponds to the so-called SU(4) Kondo effect, where the spin and the orbital degree of freedom play equivalent roles17,18 in the Kondo screening.

Figure 3: Schematic diagrams of the two limiting cases for noise in an SWNT in the Kondo regime.
figure 3

The blue line depicts the line shape of the energy-dependent transmission of the Kondo resonance. The red line depicts the part of the transmission accessible in the ‘transport window’ e Vsd. The pink dashed line is the position of the Fermi level of the reservoirs for Vsd=0. a, For the twofold-degenerate case, the effective transmission per channel is close to unity and only one channel contributes to transport, leading to a suppression of the shot noise (D(1−D) close to zero). b, For the fourfold-degenerate case, the effective transmission per channel is close to 1/2 and there are two channels, leading to an enhancement of the shot noise (D(1−D) close to 1/4).

Full size image

Unfortunately, no full out-of-equilibrium theory of the Kondo effect is available. As shown below, our experiments are carried out in a regime where T∼TK/3 and e Vsd≲3kBTK. Therefore, we have to choose a low-energy theory to understand our experiment. Essentially three different approaches can be used: the Fermi-liquid theory, the SBMF theory and the non-crossing approximation 19. Both SBMF and Fermi-liquid theory are expected to be exact in the zero-energy limit (kBT=e Vsd=0). Currently available Fermi-liquid theories20,21,22,23 provide the correct description only at very low energies and give unphysical results for the temperature and bias range of our experiment. On the other hand, the SBMF theory turns out be more robust up to the energy range of our experiment19. The non-crossing approximation is a good approximation at higher energies, and becomes inaccurate at temperatures much smaller than TK. It gives results similar to the SBMF theory at energies not too small compared with TK (ref. 19). Therefore, we use an SBMF approach, which is the simplest one available. To account for the orbital degeneracy, we use an SU(4) theory. Such a model should be regarded as the minimal one to explain our data and we should bear in mind that our samples might be in a regime where the full fourfold degeneracy is only approximately fulfilled. The SBMF has been widely used in the spin-degenerate (SU(2)) case to compute the noise in quantum dots in the Kondo regime24 and in the SU(4) case to study the conductance17. We generalize this approach here for the noise. In the SBMF approach, we still use formulae (1) and (2), replacing by , which accounts for the interactions in a self-consistent way. This is a Breit–Wigner formula with a level position and a width which explicitly depend on Vsd and T. In the SU(4) limit, we have in the symmetric case

with and , where x=e Vsd/kBTK, t=π T/TK.

From formula (3), . This contrasts with the general expression of , for which the transmission at zero energy can take any value between zero and unity. In addition, and are universal functions of x=e Vsd/kBTK and t=π T/TK. Both facts originate from electron–electron interactions. From equations (1) and (3), the conductance is fitted with only one parameter, kBTK. The outcome of the combination of equations (1), (2) and (3) is shown as solid red lines in Fig. 2a,b for kBTK=0.305 meV and kBTK=0.26 meV respectively. We find a good agreement with the experimental data using this SU(4) theory. The agreement is quantitative for the noise of SAR1 and the conductance of SAR2. The conductance of SAR1 peaks at a higher value than predicted by the SBMF, although the theoretical line corresponds to the fully symmetric case. This is probably due to the fact that the sample is not far from the mixed-valence regime25 for SAR1. Indeed, as can be seen on the linear conductance curve of Fig. 1a, the single-charge peaks slightly overlap at VG=11.26 V. The noise of SAR2 is close to the theoretical curve in the (most important) out-of-equilibrium regime, that is, . For low bias, a spurious shift less than 10% of the total noise, of about 0.4×10−27 A2 Hz−1, occurs. It probably originates from a systematic background variation for VG=11.80 V. Overall, the SBMF SU(4) theory is in much better agreement than the non-interacting resonant tunnelling theory. Both the conductance and the noise data are accounted for by a single energy scale, kBTK, even though the two actual Kondo impurities have Kondo temperatures differing by about 15%.

A scaling behaviour is a well-known property of the Kondo effect25. It has been tested only very recently in a lateral quantum dot, for the bias dependence of the conductance in the SU(2) case10. We have studied four ridges in device A and one in device B. For the five different Kondo ridges studied, we observe a scaling of G(T,0) versus T/TK and of G(1.4,Vsd) versus e Vsd/kBTK, as shown in Fig. 4a,b. For the temperature and bias dependencies, the data are very well accounted for by the empirical formula G=C0/(1+(21/s−1)(T/TK)2)s (refs 10, 26) with s=1.02±0.04 and G=G(1.4 K,0)×exp[−2(e Vsd/2.3kBTK)2]. Independently of the low-energy theory, a similar behaviour is expected for the noise19,20,21,22,23 because scaling is an essential feature of Kondo physics, linked to the fact that there is only one energy scale, TK, which controls the electronic system. We introduce I0=(2e2/h)×2D0Vsd and S0=(4e2/h)(4kBT D02+2e D0(1−D0)Vsdcoth(e Vsd/2kBT)), which are the zeroth order for the current and the noise for T/TK,e Vsd/kBTK→0 in the theory. For each Kondo ridge, the parameters D0 (D0=(h/4e2)G(T=0,Vsd=0)=2(ΓLΓR/(ΓL+ΓR)2)) and TK are obtained from the fitting of the conductance with the SBMF theory. We get the corresponding sets {Sample,Gate voltage,kBTK/e,2D0} as {A,11.80 V,0.26 mV,1}, {A,9.67 V,0.181 mV,0.94}, {A,17.65 V,0.26 mV,0.58}, {A,11.26 V, 0.305 mV,1} and {B,3.025 V,0.29 mV,0.99}. To test the scaling of the noise, we study δ S=Sexc,0−Sexc,I as a function of δ I=I0−I as shown in Fig. 4c, Sexc,(0,I) being the excess noise defined as Sexc,(0,I)=S(0,I)(Vsd)−S(0,I)(Vsd=0). We observe the same behaviour for all the five ridges, which can be fitted as δ S=(0.45±0.05)×2e δ I+0.2±0.2. The value of the slope is the central quantitative result of this letter. It is close to 1/2, which is the number predicted by the SBMF theory. For the symmetric case, this value is exact at T=0 and is a very good approximation up to T=TK/2 (see Supplementary Information). Even though TK and/or D0 can vary by as much as 40%, the noise properties of the Kondo impurity remain invariant.

Figure 4: Scaling properties of the noise of the Kondo ‘impurities’.
figure 4

a, Scaling of the temperature dependence of the zero-bias conductance. b, Scaling of the bias dependence of the conductance at 1.4 K. For the temperature (a) and bias (b) dependencies, the data are very well accounted for by the empirical formula G=C0/(1+(21/s−1)(T/TK)2)s with s=1.02 and G=G(1.4 K,0) exp[−2(e Vsd/2.3kBTK)2] (in solid lines). c, Scaling of the noise for the different ‘Kondo impurities’ measured. The line corresponds to the slope of 1/2 predicted by the SBMF. Inset: The different symbols used in the figure and their corresponding ’Kondo impurities’.

Full size image

Methods

Experimental details.

Our SWNTs are grown by chemical vapour deposition. They are localized with respect to alignment markers with an atomic force microscope or a scanning electron microscope. The contacts are made by e-beam lithography followed by evaporation of a 70-nm-thick Pd layer at a pressure of 10−8 mbar. The highly doped Si substrate (resistivity of 4–8 mΩ cm) covered with 500 nm SiO2 is used as a back-gate at low temperatures. The typical spacing between the Pd electrodes is between 200 and 500 nm. The current fluctuations in the nanotube result in voltage fluctuations along the two resistors (of 200 Ω) shown in Fig. 1b. The two signals are fed into two coaxial lines and separately amplified at room temperature by two independent sets of low-noise amplification stages (gains G1=7,268±10, G2=7,304±10, amplifiers NF SA-220F5). We calculate the cross-correlation spectrum with a spectrum analyser. Each noise point corresponds to 20 averaging runs of 40,000 spectra with a frequency span of 78.125 kHz (1,601 frequency points) and a centre frequency of 1.120 MHz or 2.120 MHz. The sensitivity is about 3×10−28 A2 Hz−1. The raw data are corrected by an offset amounting to (4.2(±0.1)+19.5(±0.2)(h/4e2)G(T,Vsd)) 10−27 A2 Hz−1, which is in very good agreement with the circuit diagram of our measurement set-up (see Supplementary Information).

Fitting details.

Throughout the letter, an SU(4) SBMF theory is used (as a minimal model). However, the SU(2) SBMF theory does not account for the data (see Supplementary Information). When fitting with the SBMF, we have interpolated the low-bias expression of with a Vsd-independent expression for |Vsd|>0.7 meV, remaining unchanged. Such an interpolation has been widely used (see for example ref. 27) to cope with the well-known phase transition problem of the SBMF approach at high bias (see Supplementary Information). Finally, when fitting the temperature dependence of the conductance for all the five ridges studied with the empirical formula described in the main section, we have found an s parameter larger than that usually found in the literature14,15 except for the experiment in ref. 26, where the SU(4) case was considered for the first time. Note however that it is distinct from the non-interacting resonant tunnelling model, which would lead to 1/T dependence for large T.