Main

Disorder is intrinsic to doped Mott insulators. Yet superconductivity in the cuprates seems surprisingly robust against impurities, much more so than what would be expected on the basis of standard Abrikosov–Gorkov theory18,19, which implies that disorder is a pair-breaking perturbation for d-wave pairing symmetry. (Other unconventional superconductors such as Sr2RuO4 with p-wave triplet pairing are indeed highly sensitive to disorder20 as expected theoretically.) Recent scanning tunnelling spectroscopy experiments10,11,12,13,14 on cuprates have led to atomic-scale insights on the response to impurities, and found that even though there are large inhomogeneous variations of the superconducting gap on the nanoscale, nevertheless the local density of states (LDOS) at low energies is remarkably homogeneous.

Here, we generalize the theory of superconductivity in doped Mott insulators based on projected wavefunctions1,6,7,8,9 to include the effect of random impurities. We find that correlations lead to a pronounced renormalization of disorder effects. This results in a much shorter healing length over which the pairing amplitude is destroyed in the vicinity of an impurity and in greatly diminished pair-breaking effects. There are several observable consequences. First, the gapless nodal quasiparticles are found to be highly robust against disorder, leading to a low-energy density of states (DOS) that is quite insensitive to impurities in the presence of correlations; see Fig. 1. Second, the point nodes in momentum space are protected in contrast to the extended arc-like regions of gapless excitations induced by disorder in the absence of correlations (Fig. 2). In contrast, the antinodal excitations near the Brillouin zone edge, which have a large gap, are much more affected by disorder compared with the nodal quasiparticles, even in the presence of correlations.

Figure 1: Spatially averaged DOS.
figure 1

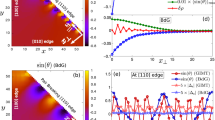
a,b, Results with (a) and without (b) correlation effects for the DOS N(ω) for various nimp (listed in b). Note that in the correlated system (a), the low-energy DOS is highly insensitive to nimp, whereas that in b, where correlations are ignored, has strong disorder dependence even at very low energies. c, The very low-energy DOS integrated over a small window |ω|≤0.02t, denoted by N(0), as a function of nimp. Results with correlations shown with open symbols (red) and plain BdG with filled symbols (blue) The average electronic density is n=0.8, impurity potential is V0=1.0t and superexchange J is chosen as described in the Methods section.

Full size image
Figure 2: Spectral function A(k,ω).
figure 2

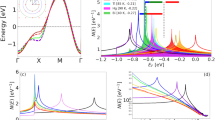
a,b, Low-energy A(k,ω), with maximum normalized to unity, for |ω|≤0.02t for 200×200 system with nimp=0.2. The results with correlations (a) show only a slight extension around the nodes, whereas the plain BdG results (b) show significant extension into ‘Fermi arcs’. c, A(k,ω) as a function of ω for nimp=0.2 in the correlated system for two momenta: the node (in red, labelled N) and the antinode (in blue, labelled AN). The input parameters are the same as in Fig. 1.

Full size image

Our starting point is the disordered t–t′–J model

The hopping of electrons with spin σ from site r to r′ on a two-dimensional square lattice is described by t the near-neighbour and t′ the next-near-neighbour hopping amplitudes. The superexchange J=4t2/U is responsible for d-wave pairing in the doped system and μ fixes the average density n=1−x with hole doping x. H acts on a Hilbert space with no doubly occupied sites, a constraint resulting from the onsite Coulomb U, the largest energy scale in the problem. The random impurity potential V (r) is V0>0 at a fraction nimp of the sites, and is zero elsewhere. We focus on weak potentials V0=t (Born scattering) as a simple model of intrinsic disorder in cuprates.

To understand how strong correlations impact disorder effects, we compare two sets of theoretical results. The first method uses the Bogoliubov–de Gennes (BdG) equations to describe the spatial inhomogeneity induced by disorder, but ignores the effects of correlations beyond the simplest Hartree–Fock level. In fact most of the theoretical work19,21,22,23 in the field, barring a few exceptions24,25, uses just such an approach. The second calculation includes the effects of both correlations and disorder. Correlations are treated using the Gutzwiller approximation to implement the no-double-occupancy constraint. This approximation has been tested9,26 in great detail in translationally invariant systems against Monte Carlo calculations7,8 that treat the constraint exactly. Here, we generalize the Gutzwiller approximation to an inhomogeneous environment, and then treat disorder using the BdG methodology. The two approaches, which will be called ‘BdG’ and ‘BdG+correlations’, are described in more detail in the Methods section.

We begin with one of our central results on the evolution of the spatially averaged DOS as a function of concentration of impurities, shown in Fig. 1. We note that there are very significant differences between the results with (Fig. 1a) and without correlations (Fig. 1b) for the DOS. The most striking observation is that the V-shaped behaviour of the low-energy DOS N(ω)≈|ω|, characteristic of a clean d-wave superconductor, survives with increasing impurity concentration nimp from 1% to 25% in the correlated case (Fig. 1a), but not in the uncorrelated case (Fig. 1b). In other words, the low-energy excitations in the strongly correlated superconductor are insensitive to disorder effects. This is also seen in Fig. 1c, where we plot N(ω) integrated over a very small window |ω|≤0.02t as a function of nimp. We see here that very little low-energy spectral weight is generated in the correlated system because the pair-breaking effect of impurities is greatly reduced in the presence of correlations, as compared with the simple BdG calculation.

In contrast to the low-energy DOS, we find that the DOS near the gap edge is strongly affected by disorder in both the correlated (Fig. 1a) and uncorrelated (Fig. 1b) systems. The sharp log singularities (‘coherence peaks’) of the clean d-wave superconductor are suppressed with increasing nimp in Fig. 1a,b, although there are some differences. The energy scale of the peaks in the DOS is shifted up slightly with increasing nimp in the correlated case, whereas it seems more or less constant in the simple BdG results.

We next explore the origin of the nodal–antinodal dichotomy seen in the angle-resolved photoemisison spectroscopy (ARPES) spectral function. In a clean d-wave superconductor, the low-energy excitations come from the vicinity of four point nodes, on the Brillouin zone diagonal, whereas those at the gap edge are dominated by the antinodes at the Brillouin zone edge. We would like to understand whether we can still make such a momentum space-based identification in the disordered systems of Fig. 1. To address this question, we compute the spectral function A(k,ω), where we Fourier transform the relative coordinate variation and spatially average the centre-of-mass variation of the Green’s function in a disordered system (see the Methods section for details).

Figure 2a,b shows the low-energy A(k,ω); this shows the k-states that contribute to the DOS in Fig. 1c. We see that the four point nodes of a clean d-wave superconductor are extended into small ‘arcs’ owing to disorder in the correlated system (Fig. 2a), whereas the uncorrelated system shows much more significant extension (Figure 2b). We should note that, within our numerical resolution, the ‘arcs’ seen here are consistent with highly anisotropic two-dimensional regions in k-space, with a small width perpendicular to the underlying Fermi surface. A similar effect has previously been found in a T-matrix calculation27 that ignores correlations. The new feature of our results is the role of correlations in suppressing the extension of the ‘arcs’.

We next compare the effect of disorder on the nodal and antinodal quasiparticle peaks in A(k,ω). In a clean d-wave superconductor, the nodal A(kN,ω) is a delta function at ω=0, whereas the antinodal A(kAN,ω) has two delta-function peaks of equal weight situated at ω=±Δ0, the maximum of the d-wave gap. Disorder leads to a broadening of these peaks, but as seen from Fig. 2c the nodal peak is much sharper in energy as compared with the antinodal one in the strongly correlated superconductor. A simple golden rule estimate of the impurity scattering rate suggests that the linewidths should scale like the DOS at the excitation energy. As we have already seen that the impurity-induced DOS in the correlated system is greatly suppressed relative to the uncorrelated BdG result at low energies, it is self-consistent that the gapless nodal states are much less affected by disorder than the gapped antinodal ones.

We next look at the inhomogeneous local pairing amplitude in the disordered superconductor to see how the presence of strong correlations affects it. This is useful to gain a deeper understanding of the above results, even though the pairing amplitude is not directly observable in experiments. The local d-wave pairing amplitude , where Δr,r′ is the bond pairing amplitude (defined in the Methods section) and ɛr,r′=1 for and −1 for .

Figure 3 shows that Δ(r) is suppressed at the location of the impurity in both the correlated and uncorrelated calculations, but the manner in which the pairing amplitude heals is markedly different in the two cases. In the correlated system (Figure 3a,c), the response is highly localized in the vicinity of the impurities, whereas in the uncorrelated system (Figure 3b,d), it is spread out over a longer distance. We note that the superexchange J in the correlated and uncorrelated calculations is chosen so as to ensure the same Δ0 in the two cases in the absence of any disorder (see caption of Fig. 3 for details). There are three distinct mechanisms that seem to underly the reduction in healing length in the correlated system. First, interactions screen the disorder potential; second, correlations lead to a mass renormalization, which is about a factor of two in the pure (non-disordered) case7,8. However, the most interesting aspect of our results is that we find that the spatially varying Gutzwiller factors are very important. Physically, the electron density is suppressed near an impurity, which reduces the constraints imposed by projection and enhances the local hopping on the bonds around the impurity. The system is consequently able to repair the damage induced by the disorder and heal the pairing amplitude over a shorter length scale.

Figure 3: Local pairing amplitude Δ(r).
figure 3

a–d, The spatial variation of Δ(r) (with maximum normalized to unity) with (a,c) and without (b,d) correlations. The four dark spots correspond to impurity sites with greatly suppressed pairing amplitude. Note that the healing length is much shorter in the correlated case. The results are for a given disorder realization with V0=1.0t and nimp=0.01, corresponding to four impurities in a 20×20 lattice, with an average electron density n=0.8. J=0.33t for the ‘BdG plus correlations’ results (a,c), whereas J=1.1t for the ‘BdG’ results ignoring correlations (b,d); these J values were chosen so that the pure system Δ0 is the same with and without correlations.

Full size image

The insensitivity of the high-temperature (Tc) superconductors to disorder has been understood up to this point as related to (1) the fact that intrinsic disorder lies off the CuO2 planes in the spacer layers, and (2) the short coherence length in the cuprates leads to a very local and inhomogeneous response21,22,28 to impurities in marked contrast to the standard Abrikosov–Gorkov theory. Our results give a completely new insight into the central role of strong correlations in leading to a shorter coherence length. They further provide an understanding of several striking experimental observations. Specifically, our results are in remarkable agreement with scanning tunnelling microscopy (STM) measurements11 that find that the very low-energy spectra do not vary from one region of the sample to another, whereas the spectra near the gap edge are very inhomogeneous. The nodal–antinodal dichotomy—with antinodal excitations strongly affected and the nodal ones relatively insensitive to disorder—captures the essential features of both ARPES15,16,17 and STM10,11,12,13,14 experiments on cuprates.

The big question that remains to be answered is: what is the underlying fundamental principle that protects the low-energy excitations against disorder in a strongly correlated superconductor? We suggest that this is related to the fact that spin-pairing underlies the strongly correlated superconductor while the impurity potential couples to charge excitations. A deeper understanding of the interplay between strong correlations and disorder is one the most challenging issues in condensed-matter physics today.

Methods

We first describe the two T=0 calculations, the results of which are reported in the paper. (1) The BdG mean-field theory that includes the inhomogeneity from the disorder, but treats interactions only at the simplest Hartree–Fock level and (2) the Gutzwiller approximation coupled with the BdG method that includes the effects of both strong correlations and of disorder. We then describe the choice of Hamiltonian parameters and give details of the calculation of the DOS and the spectral function.

The most commonly used approximation is to simply ignore the no-double-occupancy constraint and solve the BdG mean-field equations for an inhomogeneous superconductor21,22. The interaction in equation (1) is decomposed into local bond-pairing amplitudes Δr r′=J〈cr↑cr′↓−cr↓cr′↑〉/2 and Fock shifts Wr r′=J〈cr′σ†cr σ〉/2 with the density . The effective BdG Hamiltonian is then diagonalized and the fields defined above calculated self-consistently. Note that in this approach, which we label ‘BdG’, we ignore all correlation effects beyond the simple Hartree–Fock level (restricted to non-magnetic solutions so that no moment formation is allowed).

We next include the non-perturbative effects of strong correlations, over and above inhomogeneous BdG theory, as follows. The Hilbert space consists of states |Φ〉=P|Φ0〉 where the projection operator eliminates double occupancy in the state |Φ0〉. Here, we use the Gutzwiller approximation3,6 to handle projection. In the translationally invariant, clean system it has been shown that such an approximate treatment is in very good semiquantitative agreement3,6,9,26 with Monte Carlo studies of variational wavefunctions with P implemented exactly7,8.

We generalize the Gutzwiller approximation to inhomogeneous states29 by writing the expectation value of an operator in a state P|Φ0〉 as the product of a Gutzwiller factor gQ times the expectation value in |Φ0〉 so that . The standard procedure6 for calculating gQ can be generalized to keep track of the local density x(r)=1−n(r). We thus obtain the kinetic energy 〈cr σ†cr′σ〉≈gt(r,r′)〈cr σ†cr′σ〉0 and the spin correlation 〈Sr· Sr′〉≈gs(r,r′)〈Sr· Sr′〉0, with the local Gutzwiller factors given by gt(r,r′)=gt(r)gt(r′) with gt(r)=[2x(r)/(1+x(r))]1/2 and gs(r,r′)=4/[(1+x(r))(1+x(r′))].

The BdG equations are then solved for eigenvalues En and eigenvectors (un(r),vn(r)) together with local self-consistency equations for the density , the pairing amplitude and the Fock shift , where J±(r,r′)=J(3gs(r,r′)±1)/4.

Results that include correlation effects as described above are called ‘BdG+correlations’. To meaningfully compare results with and without correlations, we choose all parameters, except J, to be the same: t=1, t′=−0.25t, impurity potential V0=t, and work at the same values of average density n and impurity concentration nimp. (The scale of energy t=1 actually corresponds to t≃300 meV.) We choose the values of J=1.1t for the BdG calculation (without correlations) and J=0.33t for the ‘BdG plus correlations’ case. These choices ensure that we get the same Δ in the absence of disorder in the two calculations (Fig. 3).

Spectral function and DOS

In a disordered system, the one-particle spectral function A(r,R;ω)=−ImG(r1,r2;ω+i0+)/π depends on both the centre-of-mass R=(r1+r2)/2 and the relative coordinate r=r1−r2. STM experiments measure the LDOS N(R,ω)=A(0,R;ω). Figure 1 shows the spatially averaged DOS obtained by averaging the LDOS over the disordered system: N(ω)=〈N(R,ω)〉R. To generate a denser spectrum, we use a periodic repetition scheme with an M2 array of L2 disordered cells so that the effective size is N×N with N=M L. Typical values used are L=20 and M=10. In addition, we average over 10–15 disorder realizations.

ARPES experiments measure the occupied part of the spectral function A(k,ω). For a disordered system, we must define this as . Here, we spatially average over the ‘centre-of-mass’ variable R because ARPES data is collected over a nearly macroscopic-sized area of the sample. This is the quantity plotted in Fig. 2.

Within the Gutzwiller approximation, we obtain A(r,R;ω)=gt(r1,r2)A0(r,R;ω) with . The Gutzwiller approximation describes the coherent part of the spectral function30 that dominates A for ω values smaller than or comparable to the gap. We focus exclusively on low-energy excitations here. The higher-energy incoherent spectral weight, not accessible to the Gutzwiller approximation, can be constrained by exact sum rules and leads to p–h asymmetry30.