Main

The spectrum and eigenstates of a disorder-broadened Landau level can be studied with the well-established approach of diagonalizing the single-electron hamiltonian

where V (r) is the disorder. We choose A(r)=(0,B x) and apply periodic boundary conditions (PBCs) to a system of area A=L×L. Owing to the PBCs, the degeneracy of each Landau level, N=B L2/φ0, is an integer. Usually, in theoretical studies the magnetic field is kept fixed and the electron density ne or, equivalently, the filling factor ν=neA/N, is swept by adjusting the Fermi energy EF.

As the experiments mentioned above investigate the behaviour of various quantities in the (ne,B) plane, we need to understand how the spectrum changes when B is also tuned. Given the constraint that an integer number of fluxes must penetrate the sample, B can only change in discrete steps of φ0/L2. Therefore, we ask the following question: how do single-electron wavefunctions evolve when one more magnetic flux is inserted?

Let |i,N〉, 1≤i≤N be the eigenstates of a spin-polarized Landau level corresponding to a given disorder V (r) and a magnetic field B=N φ0/L2. The states are ordered by their energies E1<E2<⋯<EN (accidental degeneracies can be lifted with minute changes in V (r)).

To see how the wavefunctions evolve when B increases, we calculate their disorder-averaged overlaps:

where 1≤i≤N and 1≤j≤N+1 label two eigenstates of the hamiltonian (1) with the same disorder potential but different magnetic fields. The overline indicates a disorder average. In the results presented here we typically average over 1,000 disorder realizations, and show results only for the spin-polarized lowest Landau level. Similar results are expected in higher Landau levels. The disorder potential V (r) is modelled as a sum of many short-range, randomly placed gaussian scatterers. We show four sets of data, for L=250,400,500,750 nm, N=50,128,200,550 and therefore B=1.654 T for the first three data sets and 2.022 T for the last data set.

The N by N+1 matrix is almost zero everywhere except near its diagonal, as shown in Fig. 1a. Focusing on this region in Fig. 1b, we see that decreases from near unity to near zero as i increases from 1 to N, whereas is almost the mirror image of . They intersect at i/N≈1/2, that is, half-filling, where they seem to have a universal value, which is independent of N and B. These elements change most rapidly in a region near half-filling, which becomes narrower as N increases. Other matrix elements, for example, shown in Fig. 1c, exhibit a very small peak in this narrow region which we identify as the critical region.

Figure 1: Overlap between eigenstates with an extra magnetic flux quantum.
figure 1

a, Plot of the 50 by 51 overlap matrix , defined in equation (2). Only elements near the diagonal are visible. b, and versus filling factor i/N for four different sizes N=50, 128, 200 and 550. The transitions sharpen as N increases. c, Typical off-diagonal overlap matrix elements versus i/N, for the same values of N. These are much smaller than the main diagonal elements shown in b. The peak narrows as N increases.

Full size image

As the overlap of equation (2) measures the similarity of eigenstates, Fig. 1 reveals that when B increases by δB=φ0/L2, the new state appears predominantly in the centre of the disorder-broadened Landau level. This is not surprising because the extended states can enclose a large area (and thus sufficient of the extra flux) so that the effects of the δB≪B increase are not perturbative. In contrast, for localized states the effect of the extra flux is always perturbatively small. Thus, localized states at the bottom of the Landau level are little affected and keep their spectral ordering leading to large overlaps . Localized states at the top of the Landau level also keep their spectral ordering but are shifted upwards by 1, to account for the new eigenstate created in the critical region. This explains why is close to unity there.

This conclusion can also be reached using well-known results for the Hofstadter butterfly. To map into these, we tile the infinite plane with copies of the L×L system, so that the disorder V (r) becomes periodic with period L. The resulting Hofstadter problem has as a magnetic unit cell the L×L area, and thus it corresponds to B L2/φ0=q/p=N. The eigenstates of hamiltonian (1) are now magnetic Bloch waves ψi,k(r)=e−ik·rui,k(r). The integer i labels the q=N magnetic Bloch bands (MBBs) originated from a Landau level. The functions ui,k(r) satisfy generalized PBCs9. In effect, each of the N eigenstates of a Landau level of the finite-size L×L system has evolved into an MBB of the Hofstadter problem (the former are the k=0 states of the latter). As a result, we can associate with each eigenstate of the finite-size system the Chern number σi of the corresponding MBB9. σi is defined for each MBB, because energy bands Ei(k) and Ei+1(k) may only touch at discrete k points, and small changes in V (r) remove such degeneracies, as implicitly assumed when σi is calculated in refs 10, 11.

Thouless showed that localized states have zero Chern numbers12, which is easy to understand, because localized states are rather insensitive to changes in the boundary conditions used to calculate the Chern number9. This is verified by numerical calculations10,11, which find that non-zero Chern numbers appear near the centre of the Landau level, with a distribution in perfect agreement with the scaling theory of the integer quantum Hall effect13,14,15 (IQHE).

When the magnetic field is increased by φ0/L2, that is, N→N+1, a new MBB must appear in the spectrum generated from each Landau level, and thus one of the original MBBs must split into two. We now argue that only an MBB with a non-zero Chern number can do this; in other words, the new MBB (new state) appears in the critical region.

A simple proof is obtained by combining Thouless and co-workers’ famous proportionality between the Hall conductance of an MBB and its Chern number9 and Středa’s formula16 linking the Hall conductance to the change in the density of states with changing B. This gives an expression for the Chern number:

where Ni(B) is the density of states in the ith MBB. If this corresponds to a localized state, then σi=0 and this MBB cannot be the origin of the new state because its density of states stays unchanged as B varies. The new electronic state in this Landau level must therefore originate from subbands having non-zero Chern numbers.

Further proof for the above result is obtained from the semiclassical theory of Chang and Niu17,18. If δB=φ0/L2 supplies the extra flux quantum, the quantization condition of hyperorbits in the MBB reads

where m is an integer and Γi(Cm) is the contour integral over an effective gauge field along a hyperorbit Cm. Chang and Niu obtained the entire hierarchical structure of the Hofstadter butterfly by approximating the integral in equation (3) with the area of the magnetic Brillouin zone and replacing Γi(Cm) with the Chern number. If σi=0, the localized wavefunction ψi(k) can be expanded as an absolutely convergent sum of Wannier functions12, and the curvature of vanishes identically. Thus, Γi(Cm) indeed vanishes for any localized MBB regardless of the shape of Cm. In addition, as our magnetic Brillouin zone is [−π/L,π/L)×[−π/L,π/L) by construction, the left-hand side of equation (3) is found to be less than or equal to π. It follows that m=0 is the unique possibility for the MBB of a localized state, that is, such an MBB does not split into multiple MBBs when the magnetic field increases by δB (refs 17, 18). Note that both arguments are valid only if gaps between neighbouring MBBs remain open as B increases by δB. As argued, this is expected to be generically true.

A nice illustration of this property is given by the very simple ‘disorder’ potential V (r)=t[cos(2πx/L)+cos(2πy/L)]. Of course, this leads to the well-known Hofstadter butterfly spectrum, whose lower half is shown in Fig. 2. In accordance with our discussion, we are only interested in magnetic fields B corresponding to q/p=N, for large N, marked by thick lines in the figure. As expected, there are N MBBs (for even N, the two central MBBs just touch). When N→N+1, a new MBB is spawned from the central MBB(s), which is the only one with a non-zero Chern number. Indeed, if N is odd, the central subband evolves into two subbands, whereas if N is even, a new subband grows out in the centre. The outside MBBs have zero Chern numbers and indeed correspond to states localized about the bottom/top of this ‘disorder’ potential. As argued above, the spectrum of a general disorder potential also has these properties, except that typically there are several MBBs with non-zero Chern numbers, one of which will generate the new state when B increases by one magnetic flux.

Figure 2: Lower half of a Hofstadter butterfly.
figure 2

The subbands for p=1,q=N are marked by thick blue lines. The Hall conductances in units of e2/h are given for the main gaps, which never close as B∼q/p increases. The shaded blocks are typical self-similar spectra generated by an MBB when an extra flux is inserted (N→N+1). As B increases, the new spectral weight always appears in the centre of the Landau level.

Full size image

To summarize, all of these arguments prove that the new states generated in a disorder-broadened Landau level when the magnetic field increases appear predominantly in the critical region. After a state is expelled to the upper (lower) localized regions as B increases, its order from the top (bottom) of the Landau level remains essentially fixed.

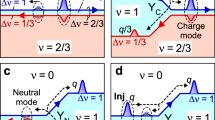
This spectral ordering is the main ingredient needed for understanding the results of recent single-electron transistor (SET) measurements19,20 that investigate the charge distribution of localized electronic states in two-dimensional electron systems2,3, as well as of measurements of mesoscopic fluctuations of two-terminal conductances4 and of Hall and longitudinal resistances5. When plotted in the (ne,B) plane, the maxima in these quantities are found to track straight lines with certain quantized values for their slopes (see Fig. 3). This suggests that such ‘stripes’ are an intrinsic aspect of IQHE phenomenology. In fact, SET and transport experiments are strikingly complementary to each other. When their results are put together, as shown schematically in Fig. 3, we get a complete picture of the stripes.

Figure 3: A schematic composite picture (computer-generated) of the stripes observed experimentally in refs 2, 3, 4, 5.
figure 3

States belonging to the nth Landau level are located between the straight lines ne=n B/φ0 and ne=(n+1)B/φ0. In the upper half of this Landau level, stripes are found to be parallel to ne=(n+1)B/φ0, whereas in the lower half, stripes are parallel to ne=n B/φ0. Near the centre of the Landau level, stripes of both slopes are visible and can cross each other. Refs 2, 3 image the stripes close to the Landau level edges, whereas refs 4, 5 image the stripes near Landau level centres.

Full size image

So far it has been unanimously agreed that these stripes are signatures of Coulomb-blockade physics in the localized states6,7,8. We now argue that the main reason for these stripes’ appearance is in fact the spectral ordering discussed above, which is a single-electron effect. Interactions do play a role through screening, as discussed below, but it is very much a secondary one.

We begin our discussion with the SET results that measure the ‘local inverse compressibility’ dμ/dne, which is a local d.c. response function dominated by localized states located under the SET tip. Consider the evolution of a maximum due to one such localized state, for example one that is found near the bottom of the nth Landau level. If the magnetic field is increased by δB=φ0/L2, n new states appear near the centres of the lower n Landau levels (counting from n=0). As a result, to bring the Fermi level back to this particular state so as to see the same maximum, ne must be increased by δne=n/L2. Thus, the maximum moves along a line of slope δne/δB=n/φ0. For a state at the top of the nth Landau level, however, the density change must be δne=(n+1)/L2, because the spectral position of this state is also shifted upwards by the new state appearing near the centre of the nth Landau level itself. Thus, maxima due to these states will have a slope of (n+1)/φ0, precisely as seen in experiments.

It is worth noting that Fig. 4. of ref. 8 shows that even if the Coulomb interaction is turned off, stripes do appear with essentially the right slopes. The authors argue that these are not in agreement with experiment because the region occupied by them increases with B, whereas in experiments we see a roughly constant number of maxima, as shown in Fig. 3. Addition of Coulomb interactions fixes this problem, but this is because of screening: their results show that the stronger the interaction, the more effective the screening, the fewer states (maxima) are seen. We therefore argue that Coulomb interactions (screening) have the secondary role of limiting the number of localized states ‘visible’ to the tip, but the stripes’ slopes are determined purely by single-electron physics.

Note that this explanation relies essentially on the fact that localized states tend to keep their spectral order with respect to the top or bottom of the Landau level. Of course, states localized about the same minimum or maximum in the disorder landscape do keep their relative spectral ordering, but it is possible that the energies of states localized in different spatial regions might cross each other as B varies. Such events must be rare, as our simulations in Fig. 1 show; in fact, we find that and get closer to 1 in the relevant interval when N increases. However, if such a rare crossing does take place for one of the states under the SET tip, the maximum will shift by δne=±1/L2 at the B value where the crossing occurs, after which the stripe resumes with the correct slope. Such jumps would be impossible to measure.

The stripes in the transport measurements have the same origin. Here, the mesoscopic fluctuations are caused by electronic states that mediate the charge transport across the Hall bar, as shown in refs 21, 22. For example, the fluctuations in the two-terminal conductance measured in ref. 4 are due to Jain–Kivelson tunnelling23 through states located in the central region of the sample. To see the same resonance, the Fermi level must be tuned to match the energy of the state mediating the tunnelling, so we expect to see the maxima following lines of quantized slopes in the (ne,B) plane for the same reasons given above. However, unlike for SET measurements, the Fermi level is now near the centre of the Landau level, where the transition between quantum Hall plateaux occurs. When an extra φ0 is inserted, there may be either n or n+1 new states below the Fermi level. As a result, we expect to see stripes with both slopes. Occasional crossings of stripes are also expected, when the states mediating their tunnelling are more than a coherence length Lφ apart, that is, there is no quantum interference between these two tunnelling events. Finally, these arguments also explain the stripes observed3 in the fractional quantum Hall effect24,25,26 (FQHE). It is well known that FQHE can be explained as the IQHE of quasiparticles27. Our explanation of the stripes in the IQHE regime is equally applicable to the FQHE regime, with electrons replaced by quasiparticles.