Abstract
Asingle neutral atom trapped by light is a promising qubit. It has weak, well-understood interactions with the environment, its internal state can be precisely manipulated1, interactions that entangle atoms can be varied from negligible to strong2,3,4 and many single atoms can be trapped near each other in an optical lattice5. This collection of features would allow for a relatively large quantum computer6 if each neutral atom qubit could be independently detected and addressed7,8,9,10. A quantum computer with even 50 qubits would allow quantum simulations that are out of the reach of classical computers11,12. So far, fewer than ten single atoms have been simultaneously imaged13. Here we demonstrate trapping and imaging of 250 single atoms in a three-dimensional optical lattice and show that imaging is highly unlikely to change the pattern of site occupancy. Our lattice spacing is large enough that, in principle, individual atoms can be addressed, which in combination with reproducible imaging should allow for verifiable filling of vacancies, execution of site-specific quantum gates and measurement of each atom’s final quantum state14,15. The lattice we use can readily be scaled to include thousands of trapped atoms.
Similar content being viewed by others
Main
The ability to spatially detect individual atoms has been a hallmark of physics in the past 20 years. Images of two-dimensional (2D) arrays of single atoms on surfaces have been made with a variety of scanning-probe microscopy techniques16. Images have been made of single particles in spontaneously formed crystals, including rotating Coulomb crystals of trapped ions in Penning traps17 and concentric shells of ions in Paul traps18, both of which have been imaged by fluorescence. Among the various imaged arrays of strongly coupled single particles, only 1D chains of ions have simple enough interactions to make viable qubits19. Such interactions are not an issue for isolated neutral atoms in optical traps, as they only interact on demand. Previous experiments have imaged 1D and 2D optical lattices with multiple neutral atoms per site20,21, and small (≤7 atom) 1D and 2D arrays of single atoms9,13. But atoms, either alone or in bunches, have not previously been spatially resolved in 3D optical lattices, where the trapping is equally tight in all directions and the sites can be far more numerous.
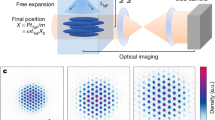
Our optical lattice is made from three overlapping pairs of laser beams, which trap neutral atoms tightly in three orthogonal directions (see the Methods section). The beams in each pair propagate at a shallow relative angle (see Fig. 1a), creating an interference pattern with a simple cubic arrangement of intensity minima 4.9 μm apart (see Fig. 1b). The lattice light is blue-detuned far from the primary atomic resonances, so the atoms are trapped at the intensity minima (see Fig. 1c).
a, The propagation directions of the lattice beams, where θ=10∘. b, The lattice sites, which form a simple cubic lattice. A random half of the lattice sites are occupied by single atoms. c, The potential along one lattice axis. Atoms are trapped near intensity minima. The lattice depth varies across the lattice because of the lattice-beam waists.
Cold caesium atoms are first collected in a magneto-optic trap. When the optical lattice is turned on around those atoms, there is initially an average of six atoms per lattice site. At each site, atoms undergo pairwise light-assisted collisions5, which can either significantly increase their kinetic energy, or cause them to form a molecule. Either way, both atoms are lost more quickly than we can observe, so that sites that are initially occupied by an even number of atoms become empty and sites that are initially odd-occupied end up with a single atom5. In the final state, a random half of the lattice sites have a single atom. After 5 ms, we shut off the magneto-optic trap light and magnetic field and turn on a set of six optical molasses laser beams to further polarization-gradient cool the trapped atoms22.
To observe where the atoms are, we image the spontaneously scattered laser cooling light onto a CCD (charge-coupled device). We use a diffraction-limited objective outside the vacuum cell. Its depth of field, 2.8 μm, is sufficiently shallow that only one plane of atoms is in focus at a time (see the Methods section). We image one plane, then focus on the next plane by axially translating the objective with a piezoelectric transducer, and then image again. Figure 2 shows three adjacent lattice planes before and after a 3 s delay. Each bright spot is due to a single atom. In the central region of the lattice, the CCD detects ∼3,300 photons per atom during the 500 ms exposure time (consistent with the calculated value). The photon number per atom varies slightly across the lattice owing to the spatial profile of the cooling beams. The diffuse light in Fig. 2 comes from trapped atoms in out-of-focus planes.
Each small bright spot is due to a single atom. We observe the lattice from the negative z axis. The haze in each photo is from atoms trapped in out-of-focus lattice planes. Atoms in the central areas of each image do not hop in 3 s, although some hopping can be seen near the edges and a few atoms are lost to background-gas collisions. The out-of-focus contribution from atoms in the central plane can in many cases be discerned in images of the adjacent planes, and vice versa. A 500 ms exposure was used. The display is a linear grey scale, with no image processing.
By comparing the image of each plane with the corresponding image 3 s later, we see that no atoms in the central ∼80 lattice sites of each plane have changed sites. Similar measurements of other lattice planes reveal no site hopping from roughly the 500 central sites. Some atoms at the shallower edges of the lattice move, and some atoms are lost to background-gas collisions, which occur at a rate per atom of 10−2 s−1.
To determine how likely it is for an atom in the central region to site-hop, we vary the depth of the confining potential due to the lattice light, U0. We model site hopping as an Arrhenius process23, where the probability that a particle hops to an adjacent site is dictated by the ratio of its temperature to an activation energy, assuming a Maxwell–Boltzmann distribution. Here U0 plays the role of the activation energy. The tunnelling probability is negligible for these lattice spacings and depths, so only thermal hopping is relevant. The energy distribution of the atoms is imposed by laser cooling (see the Methods section), which acts like a thermal bath. The model holds to the extent that the polarization-gradient cooling force remains linear in the tails of the distribution. The site hopping attempt rate, Γa, is the rate at which an atom samples the tail of its energy distribution, which is related to the laser cooling time. Because the atoms equilibrate with the cooling light and not the lattice, as in condensed-matter systems23, Γa is not directly related to the trap oscillation frequency, νosc, except that Γa must be smaller than 2νosc.
We measure the site-hopping rate in one dimension, Γh, by lowering the power in only one pair of lattice beams and counting the number of hops in a fixed time interval. We take pictures every 100 ms for 60 s and count the times an atom in the central three rows of the lattice moves from one site to another. The technique and analysis are similar to those used in real-time scanning tunnelling microscopy studies of diffusion on surfaces24, except that we constrain the hopping to one dimension. The total number of hops is normalized by the average number of atoms in these sites during the 60 s. The points in Fig. 3 show the measured hopping rate as a function of U0, which is equivalent to the conventional plot as a function of 1/T. The error bars reflect Poisson counting statistics.
In one dimension, an Arrhenius process yields  , where erfc(x) is the complementary error function and kB is Boltzmann’s constant. The solid line in Fig. 3 is a weighted least-squares fit to this model. It implies an atom temperature T∼10 μK and an attempt rate of Γa∼265 s−1, much smaller than 2νosc.
, where erfc(x) is the complementary error function and kB is Boltzmann’s constant. The solid line in Fig. 3 is a weighted least-squares fit to this model. It implies an atom temperature T∼10 μK and an attempt rate of Γa∼265 s−1, much smaller than 2νosc.
In Fig. 2, U0 at the centre of the lattice is 165 μK×kB. Extrapolating from the data in Fig. 3, the probability of a central-lattice-site atom changing sites is 5×10−6 per second of imaging. Video 1 (see the Supplementary Information) shows, in real time, atoms in this deep lattice for 20 s. There is no evident site hopping at the central sites. For Video 2 (see the Supplementary Information), the potential is reduced by a factor of 2 in all three directions, and atoms can be observed hopping between nearest-neighbour sites in the image plane, as well as hopping in and out of the image plane. Occasionally we see two atoms in adjacent sites disappear in a single frame, when one hops onto the other and they quickly collide.
We have taken a series of 50-ms-exposure images with 1.7 times the cooling intensity used in Fig. 2. These allow us to determine the reliability with which we can quickly resolve the presence or absence of an atom at a given site. To do so, we carried out least-squares fits to narrow peaks at lattice sites (see the Methods section) and made a histogram of the fit amplitudes (see Fig. 4). We infer (see the Methods section) that we can detect the presence or absence of an atom with 3×10−4 probability of error. The expected error drops to 10−7 if the most uncertain 0.2% of the atoms are reimaged, so this identification error rate can be achieved for 250 atoms in ∼0.5 s. Figure 4 shows no evidence of doubly occupied sites, confirming their absence due to the rapid light-assisted collisions of atom pairs.
The left peak corresponds to empty lattice sites, the right peak to singly occupied sites. The data are collected from five central lattice sites and 19 different atom distributions in a total of 171 pictures, each with a 50 ms exposure. The amplitudes are determined by gaussian fits to the images, taking into account differences related to site location and adjacent plane occupancy. The solid line is the sum of four gaussian functions obtained by a least-squares fit (see the Methods section).
We can image two planes at once by displacing the imaging system’s optical axis. The resultant astigmatism creates two displaced focal planes (primary and secondary), which we adjust to coincide with adjacent lattice planes. The occupation in each plane can be determined from the elongation direction of the images, as shown in Fig. 5 for three adjacent, overlapping, pairs of planes. If the atoms were cooled to better localize them, we can imagine simultaneously reconstructing the locations of all the atoms from a holographic image. To create such a hologram, the nearly collimated light after the objective lens can be made to interfere with a nearly co-linear plane wave. The interference pattern could be recorded on a CCD, and the atom locations could be determined by signal processing.
a–c, Images made by introducing astigmatism into the imaging system. The bright horizontal (vertical) line segments are due to atoms in the lattice plane closer to (farther from) the lens. Crosses indicate an atom in both planes. The images in a–c are taken of the same atom distribution with the focal planes progressively shifted towards the lens, in steps of the lattice spacing (4.9 μm). The exposure time is 250 ms.
With T=10 μK, the r.m.s. half width (Δx) of each atom is about 270 nm, which implies that the scattering rate of lattice light by the trapped atoms Γsc∼3 s−1. Next we plan to 3D Raman-sideband cool atoms to their vibrational ground state25 (Δx∼51 nm), which, with the appropriate adjustment of lattice parameters, will make Γsc<10−2 s−1. As neutral-atom gates can be executed at rates in excess of 105 s−1 (refs 9,26), this is a long enough decoherence time to allow for significant quantum computations. In our lattice, single qubit gates can be executed at individual sites without affecting other sites, using a combination of focused laser beams and microwaves14. Site-specific two-qubit Rydberg gates can be made2, using two-photon Rydberg excitation with crossed focused laser beams. The 3D lattice geometry is also amenable to the creation of cluster states that could be useful for robust one-way quantum computation4,27.
In the future, we will execute the vacancy-filling procedure described in refs 14 and 15, which combines site-selective state changes and state-selective translation. The procedure is efficient, scaling as N1/3 in 3D. It requires less than 28 motion steps for 250 atoms and can yield perfect site filling, limited only by background-gas collisions, because the filling can be checked and the procedure repeated to correct errors.
We have demonstrated the ability to non-perturbatively identify atom locations in a half-filled 500-site lattice. With further laser cooling25, we should be able to produce a manifestly zero-entropy state of 250 atoms with a very long decoherence time. Experiments with single neutral atoms have yet to match the quantum control that has been achieved over single ions, where experiments have already realized eight-qubit entanglement28,29. However, the ready scalability of neutral atoms in optical lattices makes them a promising system for the eventual realization of a quantum computer.
Methods
Lattice
The beams in each pair propagate at a relative angle of θ=10∘ and are linearly polarized perpendicular to their plane of propagation. To prevent mutual interference, the pairs are shifted in frequency relative to each other by tens of MHz (ref. 22). This also ensures effectively linear polarization everywhere22. The lattice spacing is λ/(2sin(θ/2))=4.9±0.1 μm. The lattice wavelength λ=845.5 nm and the lattice beam waist is ∼60 μm. With 60 mW of power in each beam, U0/kB=165 μK and the trap oscillation frequency is 15 kHz.
Optical system
The vacuum cell is a fused-silica box (5 cm×6 cm×7 cm with 5-mm-thick walls) allowing high-numerical-aperture optical access from six directions. An infinite-conjugate-ratio objective outside the cell collimates the light from the atoms. This is a custom-made 0.55-numerical-aperture lens with a 16 mm working distance, an 18 mm focal length, and a 140-μm-diameter field of view. A 580-mm-focal-length infinite-conjugate-ratio lens 1.3 m away forms a 32 times magnified image on a cooled back-illuminated CCD camera with on-chip multiplication gain. Stray trapping light is blocked by a narrowband interference filter.
Laser cooling
Our laser cooling light is detuned 45 MHz below the 6S1/2, F=4 to 6P3/2, F′=5 resonance in caesium. The cooling beams have small, 100 μm, waists to minimize indirect scatter from surfaces into the CCD.
Cooling depends on polarization gradients in the cooling light, and specifically on the Sisyphus effect22,30. The process works in the far-off-resonance lattice because the large a.c. Stark shifts associated with the lattice are the same for all magnetic sublevels. Still, the lattice affects the cooling because the typical spatial excursions of an atom within a lattice site exceed the polarization-gradient length scale. For the oscillations in the lattice site to not significantly wash out the cooling-light polarization gradients, the optical pumping time, τop, must be shorter than the oscillation period in the lattice, τosc. Empirical evidence for this is that the linear dependence of temperature with intensity, a prominent characteristic of polarization-gradient cooling, starts to be violated when τop∼τosc/4. The minimum site hopping, and thus we infer the minimum temperature, occurs when the cooling intensity I=44 mW cm−2, which is two to four times the minimum I that works in free space with the same detuning30. The cooling limits are different when atoms are laser cooled in a far-off-resonance lattice with a lattice constant comparable to that of the cooling light. In that case, atoms are trapped on a distance scale that is smaller than the polarization gradients, so τosc can exceed τop (ref. 22).
Image analysis
To determine how reliably we can distinguish zero from single occupancy, we consider central sites individually, thus controlling for cooling-light inhomogeneity and background-field differences. For a given site, for each of 19 different 3D atom distributions, we take nine 50 ms exposures. Around a site centre, we integrate a 4-pixel-wide swath in the y direction and use 11 pixels in the x direction to carry out a least-squares fit to a gaussian with an offset. We then repeat the procedure with x and y reversed, and average the fit amplitudes. This procedure gives a large-amplitude narrow peak when there is an in-focus atom, quickly and robustly picking it out of the variable but broader backgrounds due to out-of-focus atoms. With no in-focus atom, the fit amplitude is small (positive or negative), dominated by the noise. The fit amplitudes determine a preliminary occupancy map with an error rate of 1.0%. All of the images we have seen that are wrongly sorted by this method can be properly sorted by eye, so it should ultimately be possible to do much better with image-comparison software.
The error can also be decreased by incorporating information from adjacent planes. To demonstrate this, we image adjacent planes and distinguish four occupancy cases: an atom in the immediate foreground, an atom immediately aft, an atom fore and aft, and no atoms fore or aft. These are grouped separately, and a histogram of the amplitudes is constructed. For each occupancy case there are two well-separated peaks in the distribution, which correspond to unoccupied and singly occupied sites. To plot all cases together, we find the peak centres, and then shift and rescale the histograms so the peaks line up. We repeat the procedure for different lattice sites, shifting and rescaling to get a composite curve (Fig. 4).
The two peaks in the composite-curve fit have r.m.s. widths of 0.12 (zero) and 0.15 (one) in units of the peak separation. We find empirically that each peak fits well to two gaussians (see Fig. 4). We use these fits to extrapolate into the unoccupied centre of the histogram, and infer that within 50 ms we can discriminate the occupancy of a central lattice site with 3×10−4 error. The amplitudes from different exposures of the same arrangement of atoms are uncorrelated within the distribution for that site and occupancy case. Therefore, repeating ambiguous measurements yields much higher reliability in not much more time.
In practice, atoms can be sorted into occupancy cases using the preliminary occupancy map. We calculate that after two sorting iterations, the expected error rate due to mis-sorting is comfortably below 3×10−4. Properly sorted atoms will achieve the reduced error associated with Fig. 4.
The amplitude noise is 4.5 times the photon shot noise. We suspect that excess noise comes from the cooling light, which is a 3D standing wave that is not interferometrically stable, and so fluctuates in intensity and polarization at lattice-site centres. Detection during Raman-sideband cooling25, where a travelling wave will be scattered, will avoid this noise.
References
Levitt, M. H. Composite pulses. Prog. Nucl. Mag. Res. Spect. 18, 61–122 (1986).
Jaksch, D. et al. Fast quantum gates for neutral atoms. Phys. Rev. Lett. 85, 2208–2211 (2000).
Brennen, G. K., Caves, C. M., Jessen, P. S. & Deutsch, I. H. Quantum logic gates in optical lattices. Phys. Rev. Lett. 82, 1060–1063 (1999).
Mandel, O. et al. Controlled collisions for multi-particle entanglement of optically trapped atoms. Nature 425, 937–940 (2003).
DePue, M. T., McCormick, C., Winoto, S. L., Oliver, S. & Weiss, D. S. Unity occupation of sites in a 3D optical lattice. Phys. Rev. Lett. 82, 2262–2265 (1999).
DiVincenzo, D. P. Quantum computation. Science 270, 255–261 (1995).
Schlosser, N., Reymond, G. & Grangier, P. Collisional blockade in microscopic optical dipole traps. Phys. Rev. Lett. 89, 023005 (2002).
Schrader, D. et al. Neutral atom register. Phys. Rev. Lett. 93, 150501 (2004).
Bergamini, S. et al. Holographic generation of microtrap arrays for single atoms by use of a programmable phase modulator. J. Opt. Soc. Am. B 21, 1889–1894 (2004).
Yavuz, D. D. et al. Fast ground state manipulation of neutral atoms in microscopic optical traps. Phys. Rev. Lett. 96, 063001 (2006).
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. & Head-Gorson, M. Stimulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
Miroshnychenko, Y. et al. An atom-sorting machine. Nature 442, 151 (2006).
Vala, J. et al. Perfect pattern formation of neutral atoms in an addressable optical lattice. Phys. Rev. A 71, 032324 (2005).
Weiss, D. S. et al. Another way to approach zero entropy for a finite system of atoms. Phys. Rev. A 70, 040302(R) (2004).
Wiesendanger, R. Scanning Probe Microscopy and Spectroscopy: Methods and Applications (Cambridge Univ. Press, New York, 1994).
Bollinger, J. J. Crystalline order in laser-cooled, non-neutral ion plasmas. Phys. Plasmas 7, 7–13 (2000).
Walther, H. From a single ion to a mesoscopic system—crystallization of ions in Paul traps. Phys. Scripta T 59, 360–368 (1995).
Monroe, C., Meekhof, D. M., King, B. E., Itano, W. M. & Wineland, D. J. Demonstration of a fundamental quantum logic gate. Phys. Rev. Lett. 75, 4714–4717 (1995).
Scheunemann, R., Cataliotti, F. S., Hänsch, T. W. & Weitz, M. Resolving and addressing atoms in individual sites of a CO2-laser optical lattice. Phys. Rev. A 62, 051801(R) (2000).
Boiron, D. et al. Cold and dense cesium clouds in far-detuned dipole traps. Phys. Rev. A 57, R4106–R4109 (1998).
Winoto, S. L., DePue, M. T., Bramall, N. E. & Weiss, D. S. Laser cooling at high density in deep far-detuned optical lattices. Phys. Rev. A 59, R19–R22 (1999).
Barth, J. V. Transport of adsorbates at metal surfaces: From thermal migration to hot precursors. Surf. Sci. Rep. 40, 75–149 (2000).
Tansel, T. & Magnussen, O. M. Video STM studies of adsorbate diffusion at electrochemical interfaces. Phys. Rev. Lett. 96, 026101 (2006).
Han, D. J. et al. 3D Raman sideband cooling at high density. Phys. Rev. Lett. 85, 724–727 (2000).
Protsenko, E., Rymond, G., Schlosser, N. & Grangier, P. Operation of a quantum phase gate using neutral atoms in microscopic dipole traps. Phys. Rev. A 65, 052301 (2002).
Raussendorf, R. J. & Harrington, K. A fault-tolerant one-way quantum computer. Ann. Phys. 321, 2242–2270 (2006).
Leibfried, D. et al. Creation of a six-atom ‘Schrödinger cat’ state. Nature 438, 639–642 (2005).
Häffner, H. et al. Scalable multiparticle entanglement of trapped ions. Nature 438, 643–646 (2005).
Salomon, C., Dalibard, J., Phillips, W. D., Clairon, A. & Guellati, S. Laser cooling of cesium atoms below 3 μK. Europhys. Lett. 12, 683–688 (1990).
Acknowledgements
We acknowledge support from the US Army Research Office and DARPA.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Nelson, K., Li, X. & Weiss, D. Imaging single atoms in a three-dimensional array. Nature Phys 3, 556–560 (2007). https://doi.org/10.1038/nphys645
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys645
This article is cited by
-
One-dimensional arrays of optical dark spot traps from nested Gaussian laser beams for quantum computing
Applied Physics B (2022)
-
Quantum gas microscopy for single atom and spin detection
Nature Physics (2021)
-
Quantum gas magnifier for sub-lattice-resolved imaging of 3D quantum systems
Nature (2021)
-
An easy to construct sub-micron resolution imaging system
Scientific Reports (2020)
-
Many-body physics with individually controlled Rydberg atoms
Nature Physics (2020)