Main

A quantum memory, that is, a device for storing and retrieving quantum states, is a key component of any quantum information processor. Optical memory access is highly desirable, as it is intrinsically fast and single photons are robust, easily controlled carriers of quantum states. Although a bit of quantum information (qubit) can be stored in a single two-level system, it can be expedient to instead use long-lived collective spin excitations of an atomic ensemble12. The ensemble can then be viewed as a ‘macro-atom’, whose excitations are quantized spin waves (magnons), such that transitions between its energy levels (magnon number states) correspond to highly directional (superradiant20) photon emission or absorption6,7,12,13,14,15,16,17,18,19.

Making use of the strong coupling between magnons and a single electromagnetic mode, single photons emitted by one sample have been captured in another15,16, demonstrating the single-photon character of the captured field15, but not phase coherence between the ensembles. Two ensembles can also be correlated by joint projective measurements3,6,14. This has been used to generate coherence between two macro-atoms within a single atomic cloud14, although entanglement between the ensembles was not verified21,22. For two remote atomic ensembles, a similar projective measurement has been used to generate probabilistic, but heralded23, entanglement6. Continuous spin variables of two atomic ensembles have also been entangled by joint measurement3.

Here, instead of using projective measurements of emitted fields for two-ensemble manipulation, we directly couple two macro-atoms, A and B, via an optical resonator. After probabilistic but heralded generation of a single magnon in macro-atom A, we transfer the magnon (or, if we choose, a portion of it) to macro-atom B while suppressing the population of the photonic mode by means of quantum interference (adiabatic dark-state transfer)24,25,26. Successful transfer is verified by subsequent on-demand superradiant conversion of the magnon now stored in B into a photon. Partial transfer of the magnon creates a superposition state, where the two macro-atoms share a single spin-wave quantum. This deterministically generates magnon-number entanglement between the two ensembles, as deduced by mapping the spin waves onto light fields, and carrying out quantum-state tomography.

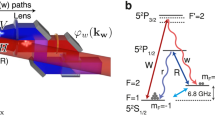
Our set-up consists of two laser-cooled ensembles, A and B, of NA,NB∼103 caesium atoms each, inside a medium-finesse () optical resonator (Fig. 1). The fundamental transverse mode of the resonator is weakly coupled to a single atom (single-atom cooperativity η≈10−3≪1), but strongly to the magnon (collective cooperativity NAη∼NBη∼1). When ensemble A is weakly illuminated with light, the detection (by a single-photon counting module) of a randomly emitted spontaneous Raman ‘write’ photon leaving the resonator heralds the creation of a quantized spin excitation (spin Dicke state12,26 or magnon19) inside the ensemble. In the following, all quantities and states are conditioned on the detection of a write photon. For sufficiently low write probability, the ideal system is thereby prepared in the product state , specifying the number of magnons inside the corresponding macro-atom. By illuminating A at a later time with a read pump ΩA that is phase-matched17 to the generated magnon and the optical-resonator mode, the magnon is converted into a read photon that can be detected on leaving the resonator (see the Supplementary Information). This mapping of collective spin excitations onto photons is key: all inferences about magnon states are derived from measured photon correlations (see the Methods section and the Supplementary Information).

Figure 1: Set-up for phase-coherent optical transfer of a spin-wave quantum between two ensembles and entanglement generation.
figure 1

a, Simplified experimental set-up. Two ensembles, A and B, are defined within a cloud of laser-cooled caesium atoms by two read pump beams, ΩA and ΩB. b, Heralded magnon generation. The collective spin excitation (magnon) is created within sample A by a weak spontaneous Raman process, , on application of a write pump beam on the transition , and heralded by the detection of a write photon on the transition escaping from the resonator. c, Spin-wave transfer via adiabatic passage in a five-level system. The write process populates the state . and are the collective couplings of the magnons to the optical resonator mode12, whereas ΩA and ΩB are pump couplings. In analogy to adiabatic passage in a three-level system27, application of a ‘counter-intuitive pulse’ sequence (see Fig. 2) transfers the system from to , corresponding to magnon transfer from A to B via the optical resonator. Population of the photonic mode (state ) and the corresponding excitation loss due to resonator decay are suppressed by quantum interference24,25. Re-absorption of the cavity photon by atoms within the cavity mode, but outside samples A and B, is avoided by blue-detuning ΩA and ΩB from atomic resonance by 20 MHz.

Full size image

If a pump beam ΩB is applied to ensemble B during read-out of ensemble A, then the photon emitted by ensemble A into the resonator can be converted into a spin wave in ensemble B. In this case, the system is described by five mutually coupled collective states (Fig. 1c), where the outermost states, and , correspond to a magnon stored in macro-atoms A and B, respectively, with no photons in the cavity (C). and are connected to each other through three intermediate states, , and , representing a collective electronic excitation in samples A and B and a photonic excitation in the cavity, respectively. Whereas and are long-lived, the intermediate states are unstable and decay via photon emission either into free space ( and ) or out of the resonator ().

It may seem difficult to transport population through several short-lived intermediate states. However, as in the simpler case of a three-level system24,25,26,27,28,29, for sufficiently strong coupling the transfer can be accomplished via adiabatic passage while suppressing the population of the intermediate unstable states by means of quantum interference. By applying a so-called counter-intuitive pulse sequence, that is, by turning on pump ΩB coupling the initially empty level first, then ramping up pump beam ΩA and subsequently ramping down ΩB, we are able to transfer the collective excitation from macro-atom A to macro-atom B while reducing decay from or (Fig. 2a). If the transfer was successful, the magnon can be directly converted into a photon by later application of pump ΩB, which is automatically phase matched to the transferred magnon.

Figure 2: Magnon transfer from macro-atom A to macro-atom B.
figure 2

a, ‘Counter-intuitive’ pulse sequence. Following preparation of a magnon in sample A by the write process, the excitation is transferred according to the sequence: (i) pump beam ΩB is turned on, (ii) pump ΩA is ramped up and subsequently (iii) pump ΩB is ramped down—between (ii) and (iii) the magnon is shared between the two samples. When ΩB is fully extinguished (iii), the magnon has been transferred to ensemble B. b,c, Applied pulse sequences of the pump beams ΩA (b) and ΩB (c). The dashed curves correspond to different read-out times from ensemble B. d, The read-photon probability density, conditioned on the preparation of a magnon in sample A, rAB, as heralded by a detected write photon near t=0. The dashed curves show the read-out probability density from macro-atom B at various read times. e, Cavity leakage with (solid red curve) and without (dotted blue curve) magnon transfer to ensemble B. Incomplete suppression of the cavity leakage indicates imperfect adiabatic transfer. f, Read-out of the B sample with (red solid curve) and without (blue dotted curve) the transfer process, demonstrating that the transfer was successful. The residual signal from B without transfer is a non-collective optical pumping signal resulting from a small overlap between sample B and the write beam applied to sample A.

Full size image

Figure 2d shows the probability of detecting a read photon, conditioned on the previous detection of a write photon emitted from ensemble A. If we apply only pump ΩA at the transfer time, tT, the A-magnon is converted into a photon with probability RA=40% (Fig. 2e, blue dotted curve) and detected with an overall efficiency of qe=0.11(2) due to losses and finite detector efficiency (see the Supplementary Information). As no collective excitations were written into sample B, no emitted photons are observed when pump ΩB is applied at a later time, tB (see Fig. 2f). However, if the adiabatic-transfer pulse sequence is applied at tT (see Fig. 2b,c), then the collective excitation is transferred to sample B, and converted into a photon when the pump beam ΩB is applied at tB. The application of ΩB also reduces the population of the cavity mode, , by destructive interference, as evident from the decrease in cavity emission during transfer at tT in Fig. 2e. The transfer efficiency, TAB, from A to B is, depending on the optical depth (collective cooperativity) of the samples NAη≃NBη≃0.4–1, between TAB=10% and 25%. A simple hamiltonian model provides good numerical agreement with this data, and predicts for large NAη, NBη.

As the magnon transfer process corresponds to the net transfer of a photon from pump beam ΩA into pump beam ΩB, the phase of the two-ensemble superposition state during the transfer is well defined and given by the phase difference φ between ΩB and ΩA. Consequently, if we interrupt the transfer process by advancing the turn-off time of ΩA until the magnon has some probability to be found in either macro-atom (adiabatic θ pulse), we expect, in the idealized limit of unit transfer efficiency and exactly one magnon in sample A before the transfer, to prepare the entangled (for ) state:

where the minus sign is characteristic of the dark state that leads to a suppression of population in the intermediate cavity state, (see Fig. 1c). The state can be viewed as an entangled state of the two ensembles or as a non-local qubit. The angles θ and φ can be adjusted by varying the relative turn-off time of, and the phase difference between, ΩA and ΩB.

State (1) implies the existence of a well-defined phase (coherence) between its two components, and . To measure this coherence, we apply, at a later time, both read pump beams ΩA and ΩB simultaneously, and vary the relative phase ϕ of ΩB and ΩA during joint read-out. For ϕ=φ (ϕ=φ+π), the read-out processes from the two macro-atoms interfere destructively (constructively), resulting in a sinusoidal dependence of the joint magnon–photon conversion efficiency on ϕ−φ. Figure 3 shows the joint conversion versus ϕ−φ for a measured ratio r=p10/p01=2.54(5), where pi j is the probability of detecting i and j photons for separate read-out of macro-atoms A and B, respectively. Although we have also measured a fringe for other values of r, for example, r=1.06(2) for the data shown in the inset, we have accumulated the largest data set and the best statistics for r=2.54 (cos2θ=0.71, or θ=32∘). The measured fringe visibility of Vphotonic=0.88(4) is in good agreement with the maximum possible value of Vmaxphotonic=2/(r1/2+r−1/2)=0.90(1). Incoherent double-excitation events could also potentially reduce the maximum possible fringe contrast; however, the reduction in our experiment falls within the statistical error.

Figure 3: Coherence of the two ensembles, A and B, after partial adiabatic transfer of a magnon.
figure 3

a, By varying the phase difference ϕ between the read pump beams during joint read-out of samples A and B for fixed preparation phase φ, we measure the coherence between the atomic ensembles after a storage time of 200 ns. The recovery efficiency, RAB (red circles), is the read photon probability inside the resonator, conditioned on the previous detection of a write photon. Error bars indicate ±1σ intervals due to the finite number of counts. No backgrounds have been subtracted. The visibility is Vphotonic=0.88(4) for the measured ratio r=p10/p01=2.54(5). The inset shows (for slightly different experimental conditions) that the individual read probabilities, p10,p01 (grey and black triangles, respectively) and r (open squares), are independent of ϕ. b, The joint read-out probability density referenced to within the cavity, conditioned on the preparation of a magnon in sample A at t≃0. c, The measured probabilities pi j for i and j photons from samples A and B, respectively, for separate read-out, referenced to within the cavity.

Full size image

Owing to imperfect single-magnon generation and magnon loss, our state also contains the two-magnon component and the vacuum component , the combination of which may spoil the entanglement inherent in the ideal state (1). The system must then be described by a density matrix. As we can convert magnons from both samples individually or jointly into photons, we can carry out state tomography in the subspace with zero or one excitations in each macro-atom, and establish bounds on the density-matrix elements. From there it is possible to verify the presence of entanglement in the full system6,23, for example, by establishing a bound on the concurrence that measures the entanglement of formation30.

We adapt the procedure developed by Chou et al. 6 for a similar system, where remote entanglement was generated by measurement. We denote the probability of finding i and j magnons in macro-atoms A and B, respectively, by mi j, whereas the probability to find the system in the subspace H1 is M=m00+m10+m01+m11=1.00(1). The concurrence can then be shown to obey , where is defined by

(See the Supplementary Information and ref. 6.) Here , GAB=m00m11/(m10m01) is closely related to the magnon–magnon cross-correlation function gAB between the ensembles (and is bounded by it from above for gAB≤1) and V is the normalized magnon coherence within H1 (see the Supplementary Information). Note that for poissonian magnon distributions in ensembles A and B we would have GAB=1 (see the Supplementary Information), whereas the coherence obeys by definition V ≤1, and consequently , so that there would be no entanglement. As the transfer process by itself cannot render subpoissonian magnon distributions in ensembles A and B, entanglement requires the preparation of a single magnon in macro-atom A before transfer (gAA<1). In a separate experiment, we have verified gAA≤gAAphotonic=0.13(8)<1.

To evaluate equation (2), we note that an upper bound on GAB is given by gABphotonic for the read photons after magnon–photon mapping (see the Methods section and the Supplementary Information). Similarly, a lower bound on is given by the detected read photon numbers referred back to within the resonator, and a lower bound on V is given by V ≥Vphotonic. From the measured values Vphotonic=0.88(4), gABphotonic=p11/(p10+p11)(p01+p11)=0.21(8) and m≥0.049(6) (see Fig. 3), we find ( without correcting for losses in the detection path), demonstrating that the two ensembles are entangled.  is primarily limited by the finite transfer and magnon–photon conversion efficiencies, or equivalently, by the value of, and bound we can place on, the vacuum component compared with the ideal state (1). Both transfer and magnon–photon conversion19 can be significantly improved by increasing the optical depth of the system.

Our scheme is well suited to deterministic generation of entanglement over short distances. In the case of entanglement generation over lossy channels (that is, long distances), post-selected schemes can be used to reduce the vacuum component and improve the available entanglement by repeated trials12.

In summary, we have demonstrated a dark-state optical bus for phase-coherent transfer of a single spin-wave quantum between two atomic ensembles. It is noteworthy that entanglement can be deterministically generated in a linear system. Using optical dipole traps to enhance the optical depth of, and separation between, the samples would result in a concomitant increase in transfer efficiency, permitting entanglement of more than two macro-atoms, and eventually multipartite entanglement on demand.

Methods

The complete sequence consists of preparing cold caesium atoms in a magneto-optical trap, turning off the trapping fields and beams in 2 ms, polarization-gradient cooling the atoms for 4 ms, optically pumping for 100 μs and then carrying out the write–transfer–read-out process repeatedly. The write–transfer–read-out process occurs once every 5 μs and is repeated 400 times, corresponding to 2 ms of data acquisition. Combined with the time required to recapture and re-cool the atoms, the entire sequence can be repeated at a rate of 15 Hz.

The two macro-atoms are each composed of approximately 103 atoms within the cavity mode waist. The distance between the ensembles is 390 μm and each sample has r.m.s. dimensions of 55 μm×55 μm×105 μm. The sample dimensions are defined in and by the cavity waist and in by the beam waist.

The relevant atomic levels referenced in Fig. 1 are the hyperfine and magnetic sublevels and .

The correlation functions for magnons are given by:

where mα is the number of magnons in macro-atom α and δμ ν is the Kronecker delta function. The photon correlation functions are given by similar expressions.

Loss in the detection path does not affect the value of a (normally ordered) correlation function31. Throughout this work, we use that fact to bound the magnon correlation functions with their counterparts measured by converting the magnons into photons and measuring photon correlation functions. In addition to loss, the photonic paths have backgrounds that act to drive the correlation functions towards unity (or 2, in the case of thermal backgrounds). As such, magnon correlation functions that are less than unity (gAA, gAB and so on) are bounded from above by their photonic counterparts.

Our digital output board has a 15 ns timing resolution, resulting in a 10∘ resolution for θ, with a jitter of 4∘ at θ=32∘ resulting from atom number variation in the two samples, and pump laser detuning drift.

We operate at a write photon number per trial nw=0.02(1) and find that the cross-correlation between the write photon and the read-out of the A-sample without transfer is gWA=30(2). This is near the fundamental limit gWAmax=1/nw≃50, indicating that the experiment is dominated by signal, and not by background.