Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Conformal invariance in two-dimensional turbulence

Nature Physics volume 2, pages 124–128 (2006)Cite this article

Abstract

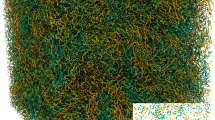
The simplicity of fundamental physical laws manifests itself in fundamental symmetries. Although systems with an infinite number of strongly interacting degrees of freedom (in particle physics and critical phenomena) are hard to describe, they often demonstrate symmetries, in particular scale invariance. In two dimensions (2D) locality often extends scale invariance to a wider class of conformal transformations that allow non-uniform rescaling. Conformal invariance enables a thorough classification of universality classes of critical phenomena in 2D. Is there conformal invariance in 2D turbulence, a paradigmatic example of a strongly interacting non-equilibrium system? Here, we show numerically that some features of a 2D inverse turbulent cascade show conformal invariance. We observe that the statistics of vorticity clusters are remarkably close to that of critical percolation, one of the simplest universality classes of critical phenomena. These results represent a key step in the unification of 2D physics within the framework of conformal symmetry.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 3: A portion of a candidate SLE trace obtained from the vorticity field.
Figure 1: Vorticity clusters.
Figure 2: Fractal dimensions and probabilities of size and boundary length for vorticity clusters.
Figure 4: The driving function is an effective diffusion process with diffusion coefficient κ=6±0.3.
Figure 5: Crossing and surrounding probability for vorticity clusters.

Similar content being viewed by others

References

  1. Kraichnan, R. H. Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423 (1967).

    Article  ADS  MathSciNet  Google Scholar 

  2. Kraichnan, R. H. & Montgomery, D. Two-dimensional turbulence. Rep. Prog. Phys. 43, 547–619 (1980).

    Article  ADS  MathSciNet  Google Scholar 

  3. Polyakov, A. M. The theory of turbulence in two dimensions. Nucl. Phys. B 396, 367–385 (1993).

    Article  ADS  MathSciNet  Google Scholar 

  4. Tabeling, P. Two-dimensional turbulence: a physicist approach. Phys. Rep. 362, 1–62 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  5. Kellay, H. & Goldburg, W. I. Two-dimensional turbulence: a review of some recent experiments. Rep. Prog. Phys. 65, 845–894 (2002).

    Article  ADS  Google Scholar 

  6. Falkovich, G., Gawedzki, K. & Vergassola, M. Particles and fields in fluid turbulence. Rev. Mod. Phys. 73, 913–975 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  7. Chen, S. et al. 57th APS Meeting of the Division of Fluid Dynamics (APS, Seattle, Washington, 2004).

    Google Scholar 

  8. Boffetta, G., Celani, A. & Vergassola, M. Inverse energy cascade in two-dimensional turbulence: Deviations from Gaussian behavior. Phys. Rev. E 61, R29–R32 (2000).

    Article  ADS  Google Scholar 

  9. Polyakov, A. M. Conformal symmetry of critical fluctuations. JETP Lett. 12, 381–383 (1970).

    ADS  Google Scholar 

  10. Belavin, A. A., Polyakov, A. M. & Zamolodchikov, A. A. Conformal field theory. Nucl. Phys. B 241, 333–380 (1984).

    Article  ADS  Google Scholar 

  11. Schramm, O. Scaling limits of loop-erased random walks and uniform spanning trees. Israel J. Math. 118, 221–288 (2000).

    Article  MathSciNet  Google Scholar 

  12. Lawler, G., Schramm, O. & Werner, W. Values of Brownian intersection exponents I: Half-plane exponents. Acta Math. 187, 237–273 (2001).

    Article  MathSciNet  Google Scholar 

  13. Lawler, G., Schramm, O. & Werner, W. Values of Brownian intersection exponents II: Plane exponents. Acta Math. 187, 275–308 (2001).

    Article  MathSciNet  Google Scholar 

  14. Lawler, G., Schramm, O. & Werner, W. Values of Brownian intersection exponents III: Two-sided exponents. Ann. Inst. H. Poincare 38, 109–123 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  15. Lawler, G., Schramm, O. & Werner, W. Conformal restriction properties. The chordal case. J. Am. Math. Soc. 16, 915–955 (2003).

    Article  Google Scholar 

  16. Lawler, G. Conformally invariant processes in the plane. Math. Surveys Monogr. 114, 1–242 (2005).

    MathSciNet  MATH  Google Scholar 

  17. Gruzberg, I. & Kadanoff, L. The Loewner equation: maps and shapes. J. Stat. Phys. 114, 1183–1198 (2004).

    Article  ADS  MathSciNet  Google Scholar 

  18. Cardy, J. SLE for theoretical physicists. Ann. Phys. 318, 81–118 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  19. Bauer, M. & Bernard, D. in Proc. NATO Advanced Study Institute on String, France, June 2004 (eds Baulieu, L., de Boer, J., Pioline, B. & Rabinovici, E.) (NATO Science Series, Vol. 208, Springer, Berlin, 2006).

    Google Scholar 

  20. Löwner, K. Untersuchungen über schlichte konforme Abbildungen des Einheitskreises. Math. Ann. 89, 103–121 (1923).

    Article  MathSciNet  Google Scholar 

  21. Bauer, M. & Bernard, D. Conformal field theories of stochastic Loewner evolutions. Commun. Math. Phys. 239, 493–521 (2003).

    Article  ADS  MathSciNet  Google Scholar 

  22. Saleur, H. & Duplantier, B. Exact determination of the percolation hull exponent in two dimensions. Phys. Rev. Lett. 58, 2325–2328 (1987).

    Article  ADS  MathSciNet  Google Scholar 

  23. Beffara, V. The dimension of the SLE curves. Preprint at <http://arxiv.org/abs/math.PR/0211322> (2002).

  24. Kondev, J. & Henley, C. L. Geometrical exponents of contour loops on random Gaussian surfaces. Phys. Rev. Lett. 74, 4580–4583 (1995).

    Article  ADS  Google Scholar 

  25. Duplantier, B. Conformally invariant fractals and potential theory. Phys. Rev. Lett. 84, 1363–1367 (2000).

    Article  ADS  MathSciNet  Google Scholar 

  26. Schramm, O. A percolation formula. Elect. Comm. Probab. 6, 115–120 (2001).

    Article  MathSciNet  Google Scholar 

  27. Cardy, J. Critical percolation in finite geometries. J. Phys. A 25, L201–L206 (1992).

    Article  ADS  MathSciNet  Google Scholar 

  28. Watts, G. A crossing probability for percolation in two dimensions. J. Phys. A 29, L363–L368 (1996).

    Article  ADS  MathSciNet  Google Scholar 

  29. Smirnov, S. Critical percolation in the plane: conformal invariance, Cardy’s formula, scaling limits. C.R. Acad. Sci. Paris I Math. 333, 239–244 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  30. Dubédat, J. Excursion decompositions for SLE6 and Watts’ crossing formula. Preprint at <http://arxiv.org/abs/math.PR/0405074> (2004).

  31. Nienhuis, B. Exact critical point and critical exponents of O(n) models in two dimensions. Phys. Rev. Lett. 49, 1062–1065 (1982).

    Article  ADS  MathSciNet  Google Scholar 

  32. Meakin, P. & Family, F. Diverging length scales in diffusion-limited aggregation. Phys. Rev. A 34, 2558–2560 (1986).

    Article  ADS  Google Scholar 

  33. Bogomolny, E. & Schmit, C. Percolation model for nodal domains of chaotic wave functions. Phys. Rev. Lett. 88, 114102 (2002).

    Article  ADS  Google Scholar 

  34. Weinrib, A. Long-correlated percolation. Phys. Rev. B 29, 387–395 (1984).

    Article  ADS  MathSciNet  Google Scholar 

  35. Falkovich, G. & Fouxon, A. Anomalous scaling of a passive scalar in turbulence and equilibrium. Phys. Rev. Lett. 94, 214502 (2005).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by grants from the European network and Israel Science foundation. G.F. thanks A. Zamolodchikov, A. Polyakov, E. Bogomolny and K. Gawedzki for useful discussions.

Author information

Authors and Affiliations

  1. Service de Physique Théorique de Saclay, CEA/CNRS, Orme des Merisiers, 91191, Gif-sur-Yvette Cedex, France

    D. Bernard

  2. Dipartimento di Fisica Generale and INFN, Università di Torino, via Pietro Giuria 1, 10125, Torino, Italy

    G. Boffetta

  3. CNRS, INLN, 1361 Route des Lucioles, 06560, Valbonne Sophia Antipolis, France

    A. Celani

  4. Physics of Complex Systems, Weizmann Institute of Science, Rehovot, 76100, Israel

    G. Falkovich

Authors
  1. D. Bernard
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. Boffetta
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Celani
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. G. Falkovich
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. Falkovich.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bernard, D., Boffetta, G., Celani, A. et al. Conformal invariance in two-dimensional turbulence. Nature Phys 2, 124–128 (2006). https://doi.org/10.1038/nphys217

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys217

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing