Abstract
The rapid growth of the human cortex during development is accompanied by the folding of the brain into a highly convoluted structure1,2,3. Recent studies have focused on the genetic and cellular regulation of cortical growth4,5,6,7,8, but understanding the formation of the gyral and sulcal convolutions also requires consideration of the geometry and physical shaping of the growing brain9,10,11,12,13,14,15. To study this, we use magnetic resonance images to build a 3D-printed layered gel mimic of the developing smooth fetal brain; when immersed in a solvent, the outer layer swells relative to the core, mimicking cortical growth. This relative growth puts the outer layer into mechanical compression and leads to sulci and gyri similar to those in fetal brains. Starting with the same initial geometry, we also build numerical simulations of the brain modelled as a soft tissue with a growing cortex, and show that this also produces the characteristic patterns of convolutions over a realistic developmental course. All together, our results show that although many molecular determinants control the tangential expansion of the cortex, the size, shape, placement and orientation of the folds arise through iterations and variations of an elementary mechanical instability modulated by early fetal brain geometry.
Similar content being viewed by others
Main
The convoluted shape of the human cerebral cortex is the result of gyrification that begins after mid-gestation1,2 (Fig. 1a); before the sixth month of fetal life, the cerebral surface is smooth. The first sulci appear as short isolated lines or triple junctions during the sixth month. These primary sulci soon elongate and branch, and secondary and tertiary sulci form, resulting in a complex pattern of gyri and sulci at birth. Some new sulci develop after birth, further complicating the pattern. Although the course and patterns of gyrification vary across individuals, the primary gyri and sulci have characteristic locations and orientations16.
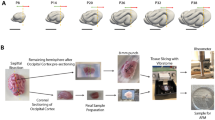
a, Gyrification of the human brain during the latter half of gestation (photographs from ref. 1, adapted with permission from Elsevier). b, A 3D-printed model of the brain is produced from a 3D MRI image of a smooth fetal brain and then used to create a pair of negative silicone moulds for casting. To mimic the constrained growth of the cortex, a replicated gel-brain (white matter) is coated with a thin layer of gel (cortex) that swells by absorbing a solvent (hexanes) over time t (t1 ≍ 4 min, t2 ≍ 9 min, t3 ≍ 16 min). c, The layered gel progressively evolves into a complex pattern of sulci and gyri during the swelling process. d, A simulation starting from a smooth fetal brain shows gyrification as a result of uniform tangential expansion of the cortical layer. The brain is modelled as a soft elastic solid and a relative tangential expansion is imposed on the cortical layer as shown at left, and the system allowed to relax to its elastic equilibrium.
Gyrification is, however, not unique to humans, and also exists in a range of primates and other species17,18. It has evolved as an efficient way of packing a large cortex into a relatively small skull with natural advantages for information processing17,19. Thus, although the functional rationale for gyrification is clear, the physiological mechanism behind gyrification has been unclear. Hypotheses include gyrogenetic theories4,20 proposing that biochemical prepatterning of the cortex controls the rise of gyri, and the axonal tension hypothesis21 proposing that axons in white matter beneath the cortex draw together densely interconnected cortical regions to form gyri. There is, however, no evidence of prepatterning that matches gyral patterns, nor is there evidence of axonal tension driving gyrification10. At present, the most likely hypothesis is also the simplest one: tangential expansion of the cortical layer relative to sublayers generates compressive stress, leading to the mechanical folding of the cortex9,10,11,12,13,14,15,22,23,24,25. This mechanical folding model produces realistic sizes and shapes of gyral and sulcal patterns15 that are presumably modulated by brain geometry26, but the hypothesis has not been tested before with real three-dimensional (3D) fetal brain geometries in a developmental setting. Here we substantiate and quantify this notion using both physical and numerical models of the brain, guided by the use of 3D magnetic resonance images (MRI) of a smooth fetal brain as a starting point.
We construct a physical simulacrum of brain folding by taking advantage of the observation that soft physical gels swell superficially when immersed in solvents. This swelling relative to the interior puts the outer layers of the gel into compression, yielding surface folding patterns qualitatively similar to sulci and gyri15. An MRI image of a smooth fetal brain at gestational week (GW) 22 (Fig. 1b; see Supplementary Methods) serves as a template for a 3D-printed cast of the brain. A mould of this form allows us to create a gel-brain (mimicking the white matter) that is then coated with a thin layer of elastomer gel (mimicking the cortical grey matter layer). When this composite gel is immersed in a solvent (see Supplementary Methods) it swells starting at the surface; this leads to superficial compression and the progressive formation of cusped sulci and smooth gyri in the cortex similar in both morphology and relative timing to those seen in real brains (Fig. 1c and Supplementary Movie 1). We note that although the mechanical creasing or sulcification instability is due to the swelling-induced compression, the effect is convoluted by the complex curvature of the initial shape.
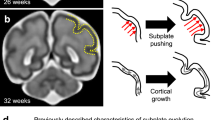
To obtain a more quantitative assessment of this process, we carry out a numerical simulation of the developing brain constructed using the same 3D fetal brain MRI (Fig. 1d) as an initial condition for the growth of a soft elastic tissue model of the brain. The model assumes that a cortical layer of thickness h is perfectly adhered to a white matter core and grows with a prescribed tangential expansion ratio g, with both tissues assumed to be soft neo-Hookean elastic solids with similar elastic moduli (see Supplementary Methods). Combining these facts with the known overall isometric growth of the brain3 yields a differential-strain-based elastic model of brain growth that we solve numerically using custom finite-element methods15. For problem parameters, we note that from GW 22 to adulthood (Supplementary Fig. 1) there is an approximately 20-fold increase in brain volume (approximately 60 ml to 1,200 ml), and a 30-fold increase in cortical area (approximately 80 cm2 to 2,400 cm2), whereas the expanding cortical layer changes little, with a typical thickness of 2.5 mm in the undeformed reference state (the deformed thickness is about 3 mm). In physiological terms, we thus assume that tangential expansion during the fetal stage extends through the cortical plate (which has a thickness of about 1–1.5 mm at GW 22) and decays rapidly in the subplate (Fig. 1d, left). The subplate diminishes during gyrification while the cortical plate thickens and develops into the cerebral cortex1,3, so that in the simulated adult brain the expanding layer corresponds to the cerebral cortex (which is about 3 mm thick in adults).
Our simple parametrization of brain growth leads to emergence of gyrification in space and time along a course similar to real brains (Fig. 1d and Supplementary Movie 2): gyrification is initiated through the formation of isolated line-like sulci (GW 26), which elongate and branch, establishing most of the patterns before birth (GW 40). After birth, brain volume still increases nearly threefold, and during this time our model shows that the gyral patterns are modified mainly by the addition of some new bends to existing gyri in agreement with longitudinal morphological analyses27. The characteristic spatiotemporal appearance of these convolutions—rounded gyri between sharply cusped sulci in a mixture of threefold junctions and S-shaped bends28—is a direct consequence of the mechanical instability induced by constrained cortical expansion. Physically, the similar stiffness of the cortex and sublayers implies that gyrification arises as a non-trivial combination of a smooth linear instability29 and a nonlinear sulcification instability30,31,32.
Sections of the physically and numerically simulated brains shown in Fig. 2a, b exhibit a bulging of gyri and deepening of sulci in a sequence resembling the observations from MRI sections. Our simulations of gyrification driven by constrained cortical expansion allow us to also measure the gyrification index (GI, defined as the ratio of the surface contour length to that of the convex hull, determined here from coronal sections as described in ref. 3). We see that there is a clear increase in the GI with developing brain volume in agreement with observations (Fig. 2c). The GI arising from our numerical simulation reaches 2.5, matching observations of adult brains. A different measure of the GI based on the cortical surface area rather than that of sections shows that the simulated adult brain has a cortical area that is approximately four times the exposed cortical area (Supplementary Fig. 1). For comparison, we also section our physical gel simulacrum that swells from an initial unpatterned state (GI = 1.07, GW 22) and see that as a function of swelling, the GI increases to about 1.55, a modest increase associated with an approximately twofold increase in brain volume, the latter state corresponding to roughly GW 30–34 (Fig. 2c and Supplementary Fig. 2). The ultimate limiting factor in our physical experiments is the inability for our gel to swell and increase its volume 20-fold like in fetal brains.
a, Planform and cross-sectional images of a physical gel-brain showing convolutional development during the swelling (folding) process that starts from an initially smooth shape (left panels) to a moderately convoluted shape (right panels). b, The coronal sections of the simulated brain (top panels) with comparisons to corresponding MRI sections35,39. c, Gyrification index as a function of brain size for real brains (data from refs 3,40), a numerically simulated brain, and a physical gel-brain. Gestational week is indicated for fetal and children brains. The initial volume of the gel-brain (≍34 ml) is scaled to match that of the simulated brain (≍57 ml). Note that in the gel experiments only the outer layer swells and therefore the volume grows less than in real brains.
Having seen that our physical and numerical experiments can capture the overall qualitative picture of how gyri form, we now turn to the question of the role of brain geometry and mechanical stresses in controlling the placement and orientations of the major and minor sulci and gyri. In Fig. 3a, we show the field of the simulated compressive stress just before the primary sulci form. Although cortical growth in our model is relatively uniform in space, the curvature of the surface is not. This yields a non-uniform stress field in the cortical layer. Thus, compressive stresses are reduced in the vicinity of highly curved convex regions, so that the first sulci appear at weakly curved or concave regions in our simulations, consistent with observations in fetal brains1,16. Furthermore, compression-induced sulci should favour their alignment perpendicular to the largest compressive stress, and indeed directions of the largest compressive stress in our model are perpendicular to the general orientations of primary gyri and sulci (Fig. 3a). Figure 3b shows that the first generations of sulci form perpendicular to the maximum compressive stress in real and simulated model brains; this correlation is particularly clear for the primary sulci in real brains.
a, A simulated stress field just before the onset of gyrification. Lines indicate the direction of maximum compressive stress and colour indicates the magnitude of the stress (red, high). General directions of primary sulci are indicated using solid arrows. A simplified scheme of the human brain17 indicating the general orientations of sulci is shown at the top right. b, View of the first generations of sulci in a numerical simulation, in real brains (MRI, different brains for GW 22, 29 and 34), and a physical gel-brain on both hemispheres, with the former two showing the inner surfaces of cortical plates. The sulcal lines (blue, simulation; green, real brain; red, experiment) are superposed on the simulated vector fields of maximum compressive stress at GW 25 and show that most sulci form perpendicular to the direction of maximum compressive stress (solid and dotted lines are perpendicular (angle >45°) and parallel (angle <45°) to the stress vector field, respectively). The percentage of sulcal length perpendicular to the stress vectors is indicated in each case. c, A folded gel-brain showing a certain lack of symmetry between the right and left hemispheres. The panel on the lower left shows nearly overlapping sets of sulcal lines obtained from three repeated tests with the same gel-brain (see Supplementary Fig. 4).
Although the shape of the initially smooth fetal brain is described by the curvature of its surface, cortical growth eventually couples the curvature and mechanical stress in non-trivial ways. In Supplementary Fig. 3 we compare the stress field and curvature at the cortical surface just before the first sulci form, and see that in highly curved regions the maximum compressive stress is perpendicular to the highest (convex) curvature. However, this does not hold at the ellipsoidal surfaces of the frontal and temporal lobes; these lobes elongate and bend towards each other as a result of cortical growth (Supplementary Fig. 3; Supplementary Movie 1 shows the analogue in our gel experiments). This reduces the compressive stress in the direction of elongation and bending, which in turn is reflected in the dominant orientations of the frontal and temporal gyri.
Although the global brain shape directs the orientations of the primary gyri, the finer details of the gyrification patterns are sensitive to variations in the initial geometry. In Fig. 3c we see that the patterns of gyri and sulci on a physical gel-brain exhibit some deviations from perfect bilateral symmetry. The hemispheres are not identical in real brains either, but we note that in our models artefacts from imaging, surface segmentation, and sample preparation can cause the two hemispheres to differ more than in reality. The sequential patterns emerging from the folding (swelling) and unfolding (drying) process also show some degree of variations (Supplementary Fig. 4), but this process is highly repeatable; indeed, the resulting gyral patterns are found to be robust and reproducible on multiple repetition of the experiment with the same gel-brain sample (lower left of Fig. 3c). The folding patterns vary in detail across samples (Supplementary Fig. 4), but they share general similarities in terms of the alignment of sulci and gyri and the inter-sulcal spacing. These experimentally derived findings corroborate numerical results; in Supplementary Fig. 5 we see the extent of variations associated with imperfections, by comparing the left and right hemispheres of the simulated brain when the simulation has been run forwards (folding) or backwards (unfolding) in time. In Supplementary Fig. 6 we compare the simulated folding of two different brains (starting from MRI images of different fetal brains) and see that the patterns in both brains are consistent with the scheme depicted in Fig. 3a.
We quantify our qualitative comparison of the similarities between real and simulated brains in Fig. 4 using morphometric techniques. Conformal mapping of the curvature vector fields (see Supplementary Methods) allows for a visual (Fig. 4a) as well as quantitative comparison (Fig. 4b), which indicates similar average alignments of curvature fields, and thus folds, in both the simulated and real brains. As a final comparison, in Fig. 4c, d we identify visually many of the named primary gyri1 from the simulated brains and compare to a real fetal brain at a similar stage, and note that our simulations can capture many of the trends quantitatively.
a, Conformal spherical mappings (see Supplementary Methods) of inner cortical surfaces of real and simulated fetal brains. b, A map of angles between the vectors of the least absolute curvature of the real and simulated brain surfaces. The angle field is computed in the spherical domain and mapped back on the real brain. In grey regions the curvature directions match and in green regions they are mismatched. Average angles and Pearson correlations between real and simulated curvature fields at GW 29 and 34 are given in the table (details in Supplementary Methods). c, All notable gyri have formed by GW 37 as identified on a real fetal brain (adapted from ref. 1 with permission from Elsevier). d, Analogous regions shown in a simulated brain driven by constrained cortical expansion. In both cases, the colouring is based on visual identification of the major gyri.
All together, by combining physical experiments and numerical simulations originating with initially smooth 3D fetal brain geometries, we have quantified a simple mechanical folding scenario for the development of convolutions in the fetal brain. Our physical gel model shows that we can capture the qualitative features of the folding patterns that are driven by a combination of surface swelling and surface geometry, setting the stage for how biology can build on this simple physical pattern-forming instability. Our numerical model is fully quantitative, based on parameters that are known by simple measurements: cortical thickness, white and grey matter tissue stiffness, brain growth and relative tangential expansion of the cortex. Together, they show that gyrification is an inevitable mechanical consequence of constrained cortical expansion; patterned gyri and sulci that are consistent with observations arise even in the absence of any patterning of cortical growth. Furthermore, although cortical expansion and brain shape couple to guide placement and orientation of gyri, the finer details of the patterns, on scales comparable to the cortical thickness, are sensitive to geometrical and mechanical perturbations. Real brains are likely to have small inter-individual variations in shape, tissue properties and growth rates, and the sensitivity of mechanical folding to such small variations could explain the variability of gyrification patterns, although the primary convolutions are consistently reproducible in their location and timing.
Our organ-level approach complements the recent emphases on the many molecular determinants underlying neuronal cell size and shape, as well patterns in their proliferation and migration4,24. These variables are functions of time and space in the cortex and the sub-ventricular zone, but ultimately feed into just two physical parameters for a given initial brain shape: relative cortical expansion and the ratio of cortical thickness/brain size15. By grounding our study on observations of fetal brain development, where these parameters are known, our work provides a quantitative basis for the proximal biophysical cause of gyrification. Our results can serve as a template for physically based morphometric studies that characterize the developing geometry of the brain surface33,34,35 in terms of variations in initial brain shape and cortical expansion. Additionally, our study sets the biophysical basis for an understanding of a range of functional neurological disorders linked to structural cortical malformations4,36 that are associated with neurogenesis and brain size (for example, ASPM and CENPJ for microcephaly4,37) and cell migration and cortex thickness (for example, GPR56 for polymicrogyria6 and RELN for lissencephaly38). With this information, a natural next step is to link the molecular determinants to the macroscopic mechanics quantitatively, and ask how brain shape and function are mutually co-regulated.
References
Griffiths, P. D., Reeves, M., Morris, J. & Larroche, J. Atlas of Fetal and Neonatal Brain MR Imaging (Mosby, 2010).
Girard, N. & Gambarelli, D. Normal Fetal Brain: Magnetic Resonance Imaging. An Atlas with Anatomic Correlations (Label Production, 2001).
Armstrong, E., Scleicher, A., Omran, H., Curtis, M. & Zilles, K. The ontogeny of human gyrification. Cereb. Cortex 5, 56–63 (1995).
Sun, T. & Hevner, R. F. Growth and folding of the mammalian cerebral cortex: from molecules to malformations. Nature Rev. Neurosci. 15, 217–232 (2014).
Lui, J. H., Hansen, D. V. & Kriegstein, A. R. Development and evolution of the human neocortex. Cell 146, 18–36 (2011).
Bae, B. et al. Evolutionarily dynamic alternative splicing of GPR56 regulates regional cerebral cortical patterning. Science 343, 764–768 (2014).
Rash, B. G., Tomasi, S., Lim, H. D., Suh, C. Y. & Vaccarino, F. M. Cortical gyrification induced by fibroblast growth factor 2 in the mouse brain. J. Neurosci. 33, 10802–10814 (2013).
Reillo, I., de Juan Romero, C., Garcia-Cabezas, M. A. & Borrell, V. A role of intermediate radial glia in the tangential expansion of the mammalian cerebral cortex. Cereb. Cortex 21, 1674–1694 (2011).
Richman, D. P., Stewart, R. M., Hutchinson, J. W. & Caviness, V. S. Jr Mechanical model of brain convolutional development. Science 189, 18–21 (1975).
Xu, G. et al. Axons pull on the brain, but tension does not drive cortical folding. J. Biomech. Eng. 132, 071013 (2010).
Toro, R. & Burnod, Y. A morphogenetic model for the development of cortical convolutions. Cereb. Cortex 15, 1900–1913 (2005).
Nie, J. et al. A computational model of cerebral cortex folding. J. Theor. Biol. 264, 467–478 (2010).
Budday, S., Raybaud, C. & Kuhl, E. A mechanical model predicts morphological abnormalities in the developing human brain. Sci. Rep. 4, 5644 (2014).
Bayly, P. V., Okamoto, R. J., Xu, G., Shi, Y. & Taber, L. A. A cortical folding model incorporating stress-dependent growth explains gyral wavelengths and stress patterns in the developing brain. Phys. Biol. 10, 016005 (2013).
Tallinen, T., Chung, J. Y., Biggins, J. S. & Mahadevan, L. Gyrification from constrained cortical expansion. Proc. Natl Acad. Sci. USA 111, 12667–12672 (2014).
Ono, M., Kubik, S. & Abernathey, C. D. Atlas of the Cerebral Sulci (Georg Thieme Verlag, 1990).
Striedter, G. F. Principles of Brain Evolution (Sinauer Associates, 2005).
Mota, B. & Herculano-Houzel, S. Cortical folding scales universally with surface area and thickness, not number of neurons. Science 349, 74–77 (2015).
Zilles, K., Palomero-Gallagher, N. & Amunts, K. Development of cortical folding during evolution and ontogeny. Trends Neurosci. 36, 275–284 (2013).
Welker, W. Why does cerebral cortex fissure and fold: a review of determinants of gyri and sulci. Cereb. Cortex 8, 3–136 (1990).
van Essen, D. C. A tension based theory of morphogenesis and compact wiring in the central nervous system. Nature 385, 313–318 (1997).
Ronan, L. et al. Differential tangential expansion as a mechanism for cortical gyrification. Cereb. Cortex 24, 2219–2228 (2014).
Holland, M. A., Miller, K. E. & Kuhl, E. Emerging brain morphologies from axonal elongation. Ann. Biomed. Eng. 43, 1640–1653 (2015).
Striedter, G. F., Srinivasan, S. & Monuki, E. S. Cortical folding: when, where, how and why? Annu. Rev. Neurosci. 38, 291–307 (2015).
Bayly, P. V., Taber, L. A. & Kroenke, C. D. Mechanical forces in cerebral cortical folding: a review of measurements and models. J. Mech. Behav. Biomed. 29, 568–581 (2013).
Todd, P. H. A geometric model for the cortical folding pattern of simple folded brains. J. Theor. Biol. 97, 529–538 (1982).
Meng, Y., Li, G., Lin, W., Gilmore, J. H. & Shen, D. Spatial distribution and longitudinal development of deep cortical sulcal landmarks in infants. NeuroImage 100, 206–218 (2014).
Li, K. et al. Gyral folding pattern analysis via surface profiling. NeuroImage 52, 1202–1214 (2010).
Biot, M. A. Mechanics of Incremental Deformations (John Wiley, 1965).
Hohlfeld, E. & Mahadevan, L. Unfolding the sulcus. Phys. Rev. Lett. 106, 105702 (2011).
Hohlfeld, E. & Mahadevan, L. Scale and nature of sulcification patterns. Phys. Rev. Lett. 109, 025701 (2012).
Tallinen, T., Biggins, J. & Mahadevan, L. Surface sulci in squeezed soft solids. Phys. Rev. Lett. 110, 024302 (2013).
Toro, R. et al. Brain size and folding of the human cerebral cortex. Cereb. Cortex 18, 2352–2357 (2008).
Germanaud, D. et al. Larger is twistier: spectral analysis of gyrification (SPANGY) applied to adult brain size polymorphism. NeuroImage 63, 1257–1272 (2012).
Lefèvre, J. et al. Are developmental trajectories of cortical folding comparable between cross-sectional datasets of fetuses and preterm newborns? Cereb. Cortex http://dx.doi.org/10.1093/cercor/bhv123 (2015).
Aronica, E., Becker, A. J. & Spreafico, R. Malformations of cortical development. Brain Pathol. 22, 380–401 (2012).
Bond, J. et al. A centrosomal mechanism involving CDK5RAP2 and CENPJ controls brain size. Nature Genet. 37, 353–355 (2005).
Hong, S. E. et al. Autosomal recessive lissencephaly with cerebellar hypoplasia is associated with human RELN mutations. Nature Genet. 26, 93–96 (2000).
Serag, A. et al. Construction of a consistent high-definition spatio-temporal atlas of the developing brain using adaptive kernel regression. NeuroImage 59, 2255–2265 (2012).
Zilles, K., Armstrong, E., Scleicher, A. & Kretschmann, H. The human pattern in gyrification in the cerebral cortex. Anat. Embryol. 170, 173–179 (1988).
Acknowledgements
We thank CSC—IT Center for Science, Finland, for computational resources and J. C. Weaver for help with 3D printing. This work was supported by the Academy of Finland (T.T.), Agence Nationale de la Recherche (ANR-12-JS03-001-01, “Modegy”) (N.G. and J.L.), the Wyss Institute for Biologically Inspired Engineering (J.Y.C. and L.M.), and fellowships from the MacArthur Foundation and the Radcliffe Institute (L.M.).
Author information
Authors and Affiliations
Contributions
T.T., J.Y.C. and L.M. conceived the model and wrote the paper. T.T. developed and performed the numerical simulations. J.Y.C. developed and performed the physical experiments. J.L. developed and performed the morphometric analyses. F.R., N.G. and J.L. provided MRI images and provided feedback on the manuscript. T.T. and L.M. coordinated the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Movie 1
Supplementary Movie (MOV 1114 kb)
Supplementary Movie 2
Supplementary Movie (MOV 1064 kb)
Rights and permissions
About this article
Cite this article
Tallinen, T., Chung, J., Rousseau, F. et al. On the growth and form of cortical convolutions. Nature Phys 12, 588–593 (2016). https://doi.org/10.1038/nphys3632
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3632
This article is cited by
-
Complex-tensor theory of simple smectics
Nature Communications (2023)
-
Mechanical hierarchy in the formation and modulation of cortical folding patterns
Scientific Reports (2023)
-
Growth anisotropy of the extracellular matrix shapes a developing organ
Nature Communications (2023)
-
Homeotic compartment curvature and tension control spatiotemporal folding dynamics
Nature Communications (2023)
-
Proliferating active matter
Nature Reviews Physics (2023)