Main

The great success in the field of topological insulators1,2 since last decade inspired the study of topological features of metals. Topological metals have non-trivial surface states and their bulk Fermi surfaces can be topologically characterized3. Among them, Dirac semimetals4,5,6 have received special attention, because they host relativistic particles, the massless Dirac fermions, in a non-relativistic set-up. In such Dirac materials, two doubly degenerate bands contact at discrete momentum points called Dirac points, and disperse linearly along all directions around these points. The four-fold degenerate Dirac points are unstable by themselves; hence, symmetry protection is necessary7. Following this guideline, several three-dimensional Dirac semimetals have been theoretically proposed, and some of them have been experimentally verified recently8,9. All of these materials have time-reversal symmetry , inversion symmetry , and certain crystalline rotation symmetry.

If some of the symmetries are broken, massless Dirac fermions can in general be destroyed. For instance, when either or is broken, each doubly degenerate band is lifted, so that the Dirac cones can split into multiple Weyl cones10. This gives birth to Weyl semimetals11,12,13,14,15,16,17, and the chiral-anomaly-related transport phenomena can be observed as a signature18,19. However, the result of both and breaking remains obscure until now. It is thus natural to ask whether Dirac fermions can still exist in the absence of both and .

In this letter, we answer the question in the affirmative, and provide a concrete example of such a Dirac semimetallic phase. We consider three-dimensional systems with the antiferromagnetic (AFM) order that breaks both and but respects their combination . The low-energy physics can be explicitly captured by the following four-band effective model

where di(k), i = 0,1, …, 5 are real functions of momentum k, and τx, y, z (σx, y, z) are Pauli matrices for orbital (spin-related AFM) basis (see Supplementary Section 3 for details). The anti-unitary symmetry satisfying is given as , where K is complex conjugation. Due to this symmetry, the last five terms in H(k) anti-commute with one another; therefore, every band must be doubly degenerate (this degeneracy holds generally for all invariant systems, see Supplementary Section 1) with energy spectrum

If one has di(q) = 0 for i = 1, …, 5 at a certain isolated momentum point k = q, then the two doubly degenerate bands must cross each other there. The resulting four-fold degenerate point k = q can be further made Dirac-like when additional constraints are enforced by crystalline symmetry.

To realize stable four-fold degenerate crossing points, the generic way is to let the pair of doubly degenerate bands carry different representations of certain symmetries in the system20,21. For our AFM model, however, there is a simpler starting point for investigation. Let us assume that the local magnetic moments are along the z axis without loss of generality. When the spin–orbit coupling (SOC) effect is ignored, d3(k) and d4(k) vanish because they correspond to spin-flip processes. Thus, the crossing points must be present in general, because with three momentum components one can tune d1(k), d2(k) and d5(k) to zero simultaneously. These points can be Dirac points as long as linear dispersion is required by certain crystalline symmetry. When SOC is included, the presence of the crossing points can still be guaranteed due to the protection of the crystalline symmetry.

In accordance with our analysis, we discover that the AFM semimetals orthorhombic CuMnAs and CuMnP22,23 can host the Dirac fermions around the Fermi level. Their crystal structure has the non-symmorphic space group D2h (Pnma) with four formula units in the primitive unit cell (see Fig. 1a, b for the structure and the first Brillouin zone). The space group consists of eight symmetry operations that can be generated by three of them: the inversion , the gliding mirror reflection of the y plane Ry = {my | (0, (1/2), 0)}, and the two-fold screw rotation along the z axis S2z = {C2z | ((1/2), 0, (1/2))}, where the two non-symmorphic symmetries Ry and S2z are important in our symmetry analysis (see Supplementary Section 2 for details).

Figure 1: The crystal structure, Brillouin zone and electronic structures of orthorhombic CuMnAs.
figure 1

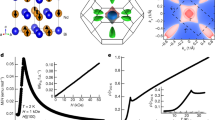
a, The crystal structure of the orthorhombic CuMnAs(P). The red arrows indicate the orientations of the magnetic moments on Mn atoms. a, b and c denote three primitive lattice vectors. b, The Brillouin zone of CuMnAs(P) and its projection to the (010) surface. c, Illustration of the screw rotation symmetry S2z = {C2z|((1/2), 0, (1/2))}. The red dashed line shows for the rotation axis. The yellow ball represents the position of the Mn atom after C2z rotation, and τ = ((1/2), 0, (1/2)) is the half translation along the (101) direction. d, The electronic structures of the orthorhombic CuMnAs along the high-symmetric lines with and without SOC. The red lines show the case without SOC, whereas the blue lines give the case with SOC in which magnetic moments of Mn atoms are along the z direction. The insets are the zoomed-in band structures in the regions of band crossings near the Fermi level. The Fermi level is set to zero.

Full size image

CuMnAs and CuMnP have been experimentally identified as room-temperature antiferromagnets previously23,24, where non-zero magnetic moments on Mn atoms with 3d electrons order antiferromagnetically (see Supplementary Section 4). The magnetic configuration breaks some symmetries from the original space group. For the most energy-favoured AFM configuration in the orthorhombic phase (see Fig. 1a), the magnetic moments on the inversion-related Mn atoms are aligned along opposite directions; therefore, both and are broken whereas still holds. If SOC is absent, spin internal space is decoupled from real space, so the spatial symmetries Ry and S2z are kept. When SOC is included, however, residual symmetries depend on the orientation of magnetic moments, for example, only S2z will survive if magnetic moments are along the z axis.

With the crystal structure and symmetry operations in mind, we begin to present our results of band structure calculations as well as effective model analysis (see Supplementary Section 9 for details of parameter choices). Figure 1d shows the electronic structures from first-principles calculations for a case where SOC is turned off in the AFM system (see Supplementary Section 5 for details). These results are consistent with the previous report23, in which band crossings are visible along high-symmetry lines. Beyond these crossings, we found an entire elliptic Dirac nodal line (DNL) on the ky = 0 plane around the Fermi level, with its centre at the X point (see Fig. 2a). We examined the band dispersions under various perturbations (see Supplementary Section 7), and found no gap opening along the nodal structure as long as Ry is present. Nevertheless, because Ry and commute on the ky = 0 plane, no rigorous symmetry protection should hold for the band crossing here in the general sense (see Supplementary Section 2). By checking the orbital composition of the bands, we finally confirmed that the existence of such a DNL in the absence of SOC is associated with the behaviours of the underlying atomic orbitals under Ry (see Supplementary Section 7). Corresponding to the DNL in the bulk, a non-trivial surface state appears inside the projection of the DNL on the (010) surface (see Fig. 2f–h). This dispersive drumhead-like surface state can be measured as a clear signature of the DNL semimetal25,26.

Figure 2: Electronic structures of CuMnAs without SOC.
figure 2

a, The electronic structure of orthorhombic CuMnAs around the Fermi level when Ry is present. The black line gives the Dirac nodal line. b, The electronic structure of orthorhombic CuMnAs when Ry is broken by shear strain. The red stars stand for the Dirac points (DPs) around the Fermi level. c,d, Schematics of the projected anisotropic Dirac cone into the (kx, kz, E) and (kx, ky, E) space reconstructed from the fitting parameters. e, Schematics of the degenerate Weyl points (WPs) with different pseudo-spin σz = ±1. The green arrows show the orbital texture. f–h, The Fermi surface contour on the (010) surface when Ry is present (f), and the corresponding electronic spectra along and when Ry is present (g,h). SS, surface state. i,j, The Fermi surface contours on the (010) surface for spin-up (i) and-down (j) states when Ry is broken. The red and white stars stand for the Weyl points with different topological charges. k, The corresponding electronic spectrum for spin-up states along . The Fermi level is set to zero. Colour scale bars in f–k relate to the local density of states, with warmer colours representing a higher density.

Full size image

When we still exclude SOC but break Ry (see Supplementary Section 8), a bandgap opens along the entire DNL except at four discrete points. One pair of the four-fold degenerate points is located on the high-symmetry line X–U, and the other pair is in the interior of the Brillouin zone. We verified the first pair as Dirac points with linear dispersions shown in Fig. 2b. The Dirac points are guaranteed by the screw rotation symmetry S2z. Unlike Ry, S2z anti-commutes with along the X–U line, so the doubly degenerate states at each k point on this line have the same S2z eigenvalues. As a result, the crossing of one pair of the doubly degenerate bands must be stable, as long as they carry different S2z eigenvalues. On the basis of ab initio results, we calculated S2z eigenvalues of the bands near the Fermi level, and the results match the symmetry argument exactly (see Supplementary Sections 2 and 6).

To check the nature of the Dirac points, we derive the low-energy effective model (see Supplementary Section 3). As we mentioned above, our AFM system without SOC is described by (we ignore the overall shift term in the following)

On the high-symmetry line X–U, the screw rotation symmetry S2z is represented by S2z = i e − i ( k z / 2 ) τ z . Expanding the Hamiltonian around one Dirac point and enforcing the symmetry constraints, we can obtain the exact Dirac-type Hamiltonian

where vij(i, j = 1,2,3) are velocity coefficients for different directions. These parameters are obtained from our calculations, and the resulting Dirac cones are anisotropic (see Fig. 2c, d). Splitting into two blocks that correspond to σz = ±1, we can decouple each Dirac cone into two Weyl cones with opposite chiralities (see Fig. 2e)

Since SOC is absent, the AFM basis σz = ±1 is almost equivalent to the physical spin basis (see Supplementary Section 1). We thus calculated the surface states on the (010) surface for each spin component, as shown in Fig. 2i–k. It is clear that Fermi arcs emerge on the surface, and they connect pairs of Weyl points with opposite chiralities. For either spin component, the chiralities of the Weyl points on the X–U line are found to be the same; therefore, it is reasonable that the other two Weyl points that carry opposite chiralities exist in the Brillouin zone such that the total chirality vanishes27.

When SOC is turned on, the presence of the crossing points sensitively depends on the orientation of the local magnetic moments on Mn atoms, as crystalline symmetries can be broken by the magnetism. If the magnetic moments are aligned along the z axis, only S2z symmetry from the space group survives. In this case, the symmetry argument for the robust crossing points along the X–U line still holds, so the four-fold degenerate points on this line are intact under the protection of S2z, while the other pair of crossing points are fully gapped (see Figs 1d and 3a). The effective model near each four-fold degenerate point is derived in the same way,

where the small perturbation terms δi, (i = 1,2,3,4) originate from SOC, which can be treated as weak coupling between the two Weyl fermions at each Dirac cone. The calculated electronic structures of AFM CuMnAs are shown in Fig. 3b–d. It is clear that no gap opens at the crossing point along the X–U line, and that non-trivial surface states appear on the (010) surface that connect two gapless points. When the magnetic moments are along other directions, S2z is broken generally, and the Dirac fermions will gain a small mass, which is proportional to the strength of SOC (see Supplementary Section 8). For orthorhombic CuMnAs and CuMnP, the typical energy dependence on the orientation of magnetic moments is relatively weak; therefore, to realize massless Dirac fermions here, several feasible methods, such as via proximity coupling28, can be taken to pin the moments along the z axis even at finite temperatures (see Supplementary Section 10 for details).

Figure 3: Electronic structures of CuMnAs with SOC.
figure 3

a, The band structure of orthorhombic CuMnAs with SOC along the X–U–X line when the orientation of magnetic moments is along the z direction. ±i are the eigenvalues of screw rotation symmetry S2z at the X point. Along the line, the eigenvalue of S2z is ±i e − i ϕ z . The blue and red colours are for different spin states respectively. b, The Fermi surface contour on the (010) surface. c,d, The corresponding electronic spectra along and . The red stars stand for the gapless points protected by the screw symmetry S2z. The Fermi level is set to zero. SS, surface state. Colour scale bars in b–d relate to the local density of states, with warmer colours representing a higher density.

Full size image

Finally we discuss experimental detections and new physics of the Dirac fermions in AFM systems. Similar to normal Dirac and Weyl semimetals, the non-trivial surface state and the orbital texture of Dirac cones could be measured as direct evidence for the Dirac fermions by angle-resolved photoemission spectroscopy29,30, since there is no net magnetization in CuMnAs and CuMnP. Furthermore, large spin Hall effects could appear due to the presence of Dirac fermions, and these relativistic particles might contribute to electric control of local magnetization in invariant antiferromagnets24. In addition, AFM fluctuations are inevitably present in CuMnAs and CuMnP, although our current treatment assumes that the magnetic configuration is frozen. If the Dirac fermions are massive, the fluctuations resemble the dynamical axion field, giving rise to exotic modulation of the electromagnetic field31. In the case where local moments are along the z axis, the fluctuations not only directly couple to the massless Dirac fermions, but also produce fermion masses through breaking crystalline symmetries. The exact description of interplay between Dirac fermions, the AFM fluctuations, and the symmetry breaking at the moment remains an open question.

Methods

Ab initio calculations.

The first-principles calculations were carried out by the density functional theory method with the projector augmented-wave method32, as implemented in the Vienna ab initio simulation package33. The Perdew–Burke–Ernzerhof exchange–correlation functional and the plane-wave basis with energy cutoff of 300 eV were employed. The lattice parameters (see Fig. 1a) were chosen from experimental values22, which are a = 6.577 Å, b = 3.854 Å and c = 7.310 Å for orthorhombic CuMnAs, and a = 6.318 Å, b = 3.723 Å and c = 7.088 Å for orthorhombic CuMnP respectively; and the inner atomic positions were allowed to be fully relaxed until the residual forces are less than 1 × 10−3 eV Å−1. The Monkhorst–Pack k points were 9 × 15 × 9, and SOC was included in self-consistent electronic structure calculations. The maximally localized Wannier functions34 were constructed to obtain the tight-binding Hamiltonian, which is used to calculate the bulk Fermi surface, surface electronic spectrum and surface states.

Data availability.

The data that support the plots within this paper and other findings of this study are available from the corresponding author on request.