Abstract
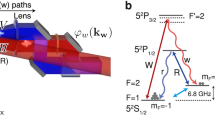
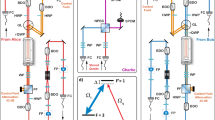
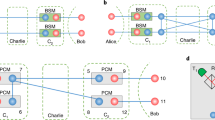
The storage of photonic entanglement is central to the achievement of long-distance quantum communication based on quantum repeaters and scalable linear optical quantum computation. Among the memory protocols reported to date, the Raman scheme has the advantages of being broadband and high-speed, resulting in a huge potential in quantum networks. To date there have been no reports on the storage of photonic polarized entanglement using the Raman protocol. Here, two storage experiments using the Raman scheme are reported: (1) heralded single-photon entanglement of the path and polarization storage in a cold atomic ensemble, and (2) polarization entanglement storage in two cold atomic ensembles. The experimental data clearly show that the quantum entanglement is preserved in this memory platform. Our work shows great promise for the establishment of quantum networks in high-speed communications.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Lvovsky, A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. Nature Photon. 3, 706–714 (2009).
Bussières, F. et al. Perspective applications of optical quantum memories. J. Mod. Opt. 60, 1519–1537 (2013).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
England, D. G. et al. High-fidelity polarization storage in a gigahertz bandwidth quantum memory. J. Phys. B. 45, 124008 (2012).
Zhang, H. J. et al. Preparation and storage of frequency-uncorrelated entangled photons from cavity-enhanced spontaneous parametric downconversion. Nature Photon. 5, 628–632 (2011).
Dai, H.-N. et al. Holographic storage of biphoton entanglement. Phys. Rev. Lett. 108, 210501 (2012).
Harris, S. E., Field, J. E. & Imamoglu, A. Nonlinear optical processes using electromagnetically induced transparency. Phys. Rev. Lett. 64, 1107–1110 (1990).
Chanelière, T. et al. Storage and retrieval of single photons transmitted between remote quantum memories. Nature 438, 833–836 (2005).
Xu, Z. et al. Long lifetime and high-fidelity quantum memory of photonic polarization qubit by lifting Zeeman degeneracy. Phys. Rev. Lett. 111, 240503 (2013).
Kozhekin, A. E., Mølmer, K. & Polzik, E. Quantum memory for light. Phys. Rev. A 62, 033809 (2000).
Nunn, J. et al. Mapping broadband single-photon wave packets into an atomic memory. Phys. Rev. A 75, 011401R (2007).
Reim, K. F. et al. Toward high-speed optical quantum memories. Nature Photon. 4, 218–221 (2010).
Reim, K. F. et al. Single-photon-level quantum memory at room temperature. Phys. Rev. Lett. 107, 053603 (2011).
Ding, D.-S. et al. Quantum storage of orbital angular momentum entanglement in an atomic ensemble. Phys. Rev. Lett. 114, 050502 (2015).
Michelberger, P. S., Champion, T. F. M., Sprague, M. R. & Kaczmarek, I. A. Interfacing GHz-bandwidth heralded single photons with a room-temperature Raman quantum memory. Preprint at http://arxiv.org/abs/1405.1470 (2014).
Bustard, P. J., Lausten, R., England, D. G. & Sussman, B. J. Toward quantum processing in molecules: a THz-bandwidth coherent memory for light. Phys. Rev. Lett. 111, 083901 (2013).
England, D. G., Bustard, P. J., Nunn, J., Lausten, R. & Sussman, B. J. From photons to phonons and back: a THz optical memory in diamond. Phys. Rev. Lett. 111, 243601 (2013).
Moiseev, S. A. & Kröll, S. Complete reconstruction of the quantum state of a single-photon wave packet absorbed by a Doppler-broadened transition. Phys. Rev. Lett. 87, 173601 (2001).
Kraus, B. et al. Quantum memory for nonstationary light fields based on controlled reversible inhomogeneous broadening. Phys. Rev. A 73, 020302(R) (2006).
Alexander, A. L., Longdell, J. J., Sellars, M. J. & Manson, N. B. Photon echoes produced by switching electric fields. Phys. Rev. Lett. 96, 043602 (2006).
Tittel, W. et al. Photon-echo quantum memory in solid state systems. Laser Photon. Rev. 4, 244–267 (2010).
Afzelius, M., Simon, C., De Riedmatten, H. & Gisin, N. Multimode quantum memory based on atomic frequency combs. Phys. Rev. A 79, 052329 (2009).
Buchler, B. C., Hosseini, M., Hetet, G., Sparkes, B. M. & Lam, P. K. Precision spectral manipulation of optical pulses using a coherent photon echo memory. Opt. Lett. 35, 1091–1093 (2010).
Hosseini, M., Sparkes, B. M., Campbell, G., Lam, P. K. & Buchler, B. C. High efficiency coherent optical memory with warm rubidium vapour. Nature Commun. 2, 174 (2011).
Fiore, V. et al. Storing optical information as a mechanical excitation in a silica optomechanical resonator. Phys. Rev. Lett. 107, 133601 (2011).
Julsgaard, B., Sherson, J., Cirac, J. I., Fiurašek, J. & Polzik, E. S. Experimental demonstration of quantum memory for light. Nature 432, 482–486 (2004).
Julsgaard, B., Kozhekin, A. & Polzik, E. S. Experimental long-lived entanglement of two macroscopic objects. Nature 413, 400–403 (2001).
Choi, K. S., Deng, H., Laurat, J. & Kimble, H. J. Mapping photonic entanglement into and out of a quantum memory. Nature 452, 67–71 (2008).
Saglamyurek, E. et al. Broadband waveguide quantum memory for entangled photons. Nature 469, 512–515 (2011).
Clausen, C. et al. Quantum storage of photonic entanglement in a crystal. Nature 469, 508–511 (2011).
Liu, Y., Wu, J.-H., Shi, B.-S. & Guo, G.-C. Realization of a two-dimensional magneto-optical trap with a high optical depth. Chinese Phys. Lett. 29, 024205 (2012).
Kuzmich, A. et al. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 423, 731–734 (2003).
Ding, D.-S., Zhou, Z.-Y., Shi, B.-S. & Guo, G.-C. Single-photon-level quantum image memory based on cold atomic ensembles. Nature Commun 4, 2527 (2013).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Chen, S. et al. Demonstration of a stable atom–photon entanglement source for quantum repeaters. Phys. Rev. Lett. 99, 180505 (2007).
Liao, K. et al. Subnatural-linewidth polarization-entangled photon pairs with controllable temporal length. Phys. Rev. Lett. 112, 243602 (2014).
Hamel, D. R. et al. Direct generation of three-photon polarization entanglement. Nature Photon. 8, 801–807 (2014).
Barz, S., Cronenberg, G., Zeilinger, A. & Walther, P. Heralded generation of entangled photon pairs. Nature Photon. 4, 553–556 (2010).
Wagenknecht, C. et al. Experimental demonstration of a heralded entanglement source. Nature Photon. 4, 549–552 (2010).
Surmacz, K. et al. Efficient spatially resolved multimode quantum memory. Phys. Rev. A 78, 033806 (2008).
Zhao, B. et al. A millisecond quantum memory for scalable quantum networks. Nature Phys. 5, 95–99 (2008).
Bao, X.-H. et al. Efficient and long-lived quantum memory with cold atoms inside a ring cavity. Nature Phys. 8, 517–521 (2012).
Radnaev, A. G. et al. A quantum memory with telecom-wavelength conversion. Nature Phys. 6, 894–899 (2010).
Heinze, G., Hubrich, C. & Halfmann, T. Stopped light and image storage by electromagnetically induced transparency up to the regime of one minute. Phys. Rev. Lett. 111, 033601 (2013).
Acknowledgements
The authors thank Yuan Sun for reading and commenting on this manuscript. This work was supported by the National Fundamental Research Program of China (grant no. 2 011CBA00200), the National Natural Science Foundation of China (grants nos. 11174271, 61275115 and 61435011), the Youth Innovation Fund from University of Science and Technology of China (grant no. ZC 9850320804) and the Innovation Fund from Chinese Academy of Sciences.
Author information
Authors and Affiliations
Contributions
B.S.S. conceived the idea and experiment. W.Z. and D.S.D. designed and carried out the experiments with assistance from Z.Y.Z. and S.S. D.S.D. and W.Z. carried out data analysis. D.S.D. wrote the manuscript. B.S.S. and G.C.G. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 527 kb)
Rights and permissions
About this article
Cite this article
Ding, DS., Zhang, W., Zhou, ZY. et al. Raman quantum memory of photonic polarized entanglement. Nature Photon 9, 332–338 (2015). https://doi.org/10.1038/nphoton.2015.43
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2015.43
This article is cited by
-
Entangling motional atoms and an optical loop at ambient condition
npj Quantum Information (2023)
-
Fast, noise-free atomic optical memory with 35-percent end-to-end efficiency
Communications Physics (2023)
-
Optimizing Raman quantum memory with dynamic phase
Science China Information Sciences (2023)
-
High-performance cavity-enhanced quantum memory with warm atomic cell
Nature Communications (2022)
-
Lifetime reductions and read-out oscillations due to imperfect initial level preparations of atoms in a long-lived DLCZ-like quantum memory
Applied Physics B (2022)