Abstract
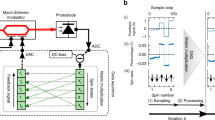
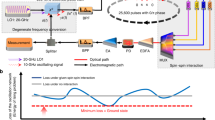
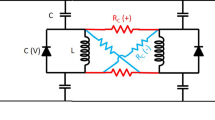
Finding the ground states of the Ising Hamiltonian1 maps to various combinatorial optimization problems in biology, medicine, wireless communications, artificial intelligence and social network. So far, no efficient classical and quantum algorithm is known for these problems and intensive research is focused on creating physical systems—Ising machines—capable of finding the absolute or approximate ground states of the Ising Hamiltonian2,3,4,5,6. Here, we report an Ising machine using a network of degenerate optical parametric oscillators (OPOs). Spins are represented with above-threshold binary phases of the OPOs and the Ising couplings are realized by mutual injections7. The network is implemented in a single OPO ring cavity with multiple trains of femtosecond pulses and configurable mutual couplings, and operates at room temperature. We programmed a small non-deterministic polynomial time-hard problem on a 4-OPO Ising machine and in 1,000 runs no computational error was detected.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Barahona, F. On the computational complexity of Ising spin glass models. J. Phys. A 15, 3241 (1982).
Kirkpatrick, S., Gelatt, D. Jr & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–680 (1983).
Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 58, 5355 (1998).
Santoro, G. E., Martoak, R., Tosatti, E. & Car, R. Theory of quantum annealing of an Ising spin glass. Science 295, 2427–2430 (2002).
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–475 (2001).
Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).
Wang, Z., Marandi, A., Wen, K., Byer, R. L. & Yamamoto, Y. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 88, 063853 (2013).
Kitchen, D. B., Decornez, H., Furr, J. R. & Bajorath, J. Docking and scoring in virtual screening for drug discovery: methods and applications. Nature Rev. Drug Discov. 3, 935–949 (2004).
Witten, I. H., Frank, E. & Hall, M. A. Data Mining: Practical Machine Learning Tools and Techniques (Morgan Kaufmann, 2005).
Papadimitriou, C. H. & Steiglitz, K. Combinatorial Optimization: Algorithms and Complexity (Courier Dover, 1998).
Hochbaum, D. S. Approximation Algorithms for NP-hard Problems (PWS, 1996).
Goemans, M. X. & Williams, D. P. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. J. ACM 42, 1115–1145 (1995).
Adleman, L. M. Molecular computation of solutions to combinatorial problems. Science 266, 1021–1023 (1994).
Wu, K., de Abajo, J. G., Soci, C., Shum, P. P. & Zheludev, N. I. An optical fiber network oracle for NP-complete problems. Light 3, e147 (2014).
Dickson, N. G. et al. Thermally assisted quantum annealing of a 16-qubit problem. Nature Commun. 4, 1903 (2013).
Ronnow, T. F. et al. Defining and detecting quantum speedup. Science 345, 420–424 (2014).
Marandi, A., Leindecker, N. C., Pervak, V. Byer, R. L. & Vodopyanov, K. L. Coherence properties of a broadband femtosecond mid-IR optical parametric oscillator operating at degeneracy. Opt. Express 20, 7255–7262 (2012).
Roslund, J., De Araujo, R. M., Jiang, S., Fabre, C. & Treps, N. Wavelength-multiplexed quantum networks with ultrafast frequency combs. Nature Photon. 8, 109–113 (2014).
Marandi, A., Leindecker, N. C., Vodopyanov, K. L. & Byer R. L. All-optical quantum random bit generation from intrinsically binary phase of parametric oscillators. Opt. Express 20, 19322–19330 (2012).
Binder, K. & Young, A. P. Spin glasses: experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 58, 801 (1986).
Ising, E. Beitrag zur Theorie des Ferromagnetismus. Zeitschrift für Physik A, Hadrons and Nuclei 31, 253–258 (1925).
Kim, K. et al. Quantum simulation of frustrated Ising spins with trapped ions. Nature 465, 590–593 (2010).
Simon, J. et al. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 472, 307–312 (2011).
Utsunomiya, S., Takata, K. & Yamamoto, Y. Mapping of Ising models onto injection-locked laser systems. Opt. Express 19, 18091–18108 (2011).
Nabors, C. D., Yang, S. T., Day, T. & Byer, R. L. Coherence properties of a doubly-resonant monolithic optical parametric oscillator. J. Opt. Soc. Am. B 7, 815–820 (1990).
Wu, L., Kimble, H. J., Hall, J. L. & Wu, H. Generation of squeezed states by parametric down conversion. Phys. Rev. Lett. 57, 2520 (1986).
Graham, R. in Coherence and Quantum Optics (eds Mandel, L. & Wolf, E.) 851–872 (Springer, 1973).
Wolinsky, M. & Carmichael, H. J. Quantum noise in the parametric oscillator: from squeezed states to coherent-state superpositions. Phys. Rev. Lett. 60, 1836 (1988).
Gottesman, D. The Heisenberg representation of quantum computers. Preprint at http://arxiv.org/abs/quant-ph/9807006 (1998).
Galluccio, A., Loebl, M. & Vondrk, J. New algorithm for the Ising problem: partition function for finite lattice graphs. Phys. Rev. Lett. 84, 5924 (2000).
Acknowledgements
The authors thank S.E. Harris, H. Mabuchi, M. Armen, S. Utsunomiya, S. Tamate, K. Yan and Y. Haribara for discussions and K. Ingold, C.W. Rudy, C. Langrock and K. Urbanek for experimental support. The work is supported by the FIRST Quantum Information Processing project.
Author information
Authors and Affiliations
Contributions
A.M. and Y.Y. conceived the idea and designed the experiment. A.M. and K.T. carried out the experiment. Z.W. performed the numerical simulations. Y.Y. and R.L.B. guided the work. A.M. wrote the manuscript, with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 2667 kb)
Rights and permissions
About this article
Cite this article
Marandi, A., Wang, Z., Takata, K. et al. Network of time-multiplexed optical parametric oscillators as a coherent Ising machine. Nature Photon 8, 937–942 (2014). https://doi.org/10.1038/nphoton.2014.249
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2014.249
This article is cited by
-
Observation of distinct phase transitions in a nonlinear optical Ising machine
Communications Physics (2023)
-
Highly reconfigurable oscillator-based Ising Machine through quasiperiodic modulation of coupling strength
Scientific Reports (2023)
-
A spinwave Ising machine
Communications Physics (2023)
-
Photonic elementary cellular automata for simulation of complex phenomena
Light: Science & Applications (2023)
-
Critical parametric quantum sensing
npj Quantum Information (2023)