Abstract
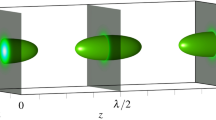
The laser beam has become an indispensable tool for the controllable manipulation and transport of microscopic objects in biology, physical chemistry and condensed matter physics. In particular, ‘tractor’ laser beams can draw matter towards a laser source and perform, for instance, all-optical remote sampling. Recent advances in lightwave technology have already led to small-scale experimental demonstrations of tractor beams1,2,3,4. However, the realization of long-range tractor beams has not gone beyond the realm of theoretical investigations5,6,7,8,9. Here, we demonstrate the stable transfer of gold-coated hollow glass spheres against the power flow of a single inhomogeneously polarized laser beam over tens of centimetres. Additionally, by varying the polarization state of the beam we can stop the spheres or reverse the direction of their motion at will.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Lee, S-H., Roichman, Y. & Grier, D. Optical solenoid beams. Opt. Express 18, 6988–6993 (2010).
Ruffner, D. B. & Grier, D. G. Optical conveyors: a class of active tractor beams. Phys. Rev. Lett. 109, 163903 (2012).
Brzobohatý, O. et al. Experimental demonstration of optical transport, sorting and self-arrangement using a ‘tractor beam’. Nature Photon. 7, 123–127 (2013).
Kajorndejnukul, V., Ding, W., Sukhov, S. & Dogariu, A. Linear momentum increase and negative optical forces at dielectric interface. Nature Photon. 7, 787–790 (2013).
Marston, P. L. Axial radiation force of a Bessel beam on a sphere and direction reversal of the force. J. Acoust. Soc. Am. 120, 3518–3524 (2006).
Sukhov, S. & Dogariu, A. Negative nonconservative forces: optical ‘tractor beams’ for arbitrary objects. Phys. Rev. Lett. 107, 203602 (2011).
Saenz, J. Laser tractor beams. Nature Photon. 5, 514–515 (2011).
Chen, J., Ng, J., Lin, Z. & Chan, C. T. Optical pulling force. Nature Photon. 5, 531–534 (2011).
Dogariu, A., Sukhov, S. & Sáenz, J. J. Optically induced ‘negative forces’. Nature Photon. 7, 24–27 (2013).
Gahagan, K. T. & Swartzlander Jr., G. A. Optical vortex trapping of particles. Opt. Lett. 21, 827–829 (1996).
Bowman, R. W. & Padgett, M. J. Optical trapping and binding. Rep. Prog. Phys. 76, 1–28 (2013).
Grier, D. G. A revolution in optical manipulation. Nature 424, 810–816 (2003).
Ashkin, A. & Dziedzic, J. M. Optical levitation in high vacuum. Appl. Phys. Lett. 28, 333–335 (1976).
Peterman, E. J. G., Gittes, F. & Schmidt, C. F. Laser-induced heating in optical traps. Biophys. J. 84, 1308–1316 (2003).
Preining, O. in Aerosol Science (ed. Davies, C. N.) Ch. V, 111–135 (Academic, 1966).
Phuoc, T. X. A comparative study of the photon pressure force, the photophoretic force, and the adhesion von der Waals force. Opt. Commun. 245, 27–35 (2005).
Rohatschek, H. Semi-empirical model of photophoretic forces for the entire range of pressures. J. Aerosol Sci. 26, 717–734 (1995).
Wurm, G. & Krauss, O. Dust eruptions by photophoresis and solid state greenhouse effects. Phys. Rev. Lett. 96, 134301 (2006).
Yalamov, Yu. I., Kutukov, V. B. & Shchukin, E. R. Theory of the photophoretic motion of the large-size volatile aerosol particle. J. Colloid Interface Sci. 57, 564–571 (1976).
Hidy, G. M. & Brock, J. R. Photophoresis and the descent of particles into the lower stratosphere. J. Geophys. Res. 72, 455–460 (1967).
Shvedov, V. G. et al. Giant optical manipulation. Phys. Rev. Lett. 105, 118103 (2010).
Mackowski, D. W. Photophoresis of aerosol particles in the free molecular and slip-flow regimes. Int. J. Heat Mass Transfer 32, 843–854 (1989).
Zulehner, W. & Rohatschek, H. Representation and calculation of photophoretic forces and torques. J. Aerosol Sci. 26, 201–210 (1995).
Yalamov, Yu. I. & Khasanov, A. S. Photophoresis of coarse aerosol particles with nonuniform thermal conductivity. Tech. Phys. 43, 347–352 (1998).
Dusel, P. W., Kerker, M. & Cooke, D. D. Distribution of absorption centers within irradiated spheres. J. Opt. Soc. Am. 69, 55–59 (1979).
Esseling, M., Rose, P., Alpmann, C. & Denz, C. Photophoretic trampoline—interaction of single airborne absorbing droplets with light. Appl. Phys. Lett. 101, 131115 (2012).
Shvedov, V. G., Hnatovsky, C., Rode, A. V. & Krolikowski, W. Robust trapping and manipulation of airborne particles with a bottle beam. Opt. Express 19, 17350–17356 (2011).
Shvedov, V. G., Hnatovsky, C., Eckerskorn, N., Rode, A. V. & Krolikowski, W. Polarization-sensitive photophoresis. Appl. Phys. Lett. 101, 051106 (2012).
Soong, C. Y., Li, W. K., Liu, C. H. & Tzeng, P. Y. Theoretical analysis for photophoresis of a microscale hydrophobic particle in liquids. Opt. Express 18, 2168–2182 (2010).
Rakic, A. D., Djurisic, A. B., Elazar, J. M. & Majewski, M. L. Optical properties of metallic films for vertical-cavity optoelectronics devices. Appl. Opt. 37, 5271–5283 (1998).
Acknowledgements
The authors acknowledge support from the Australian Research Council.
Author information
Authors and Affiliations
Contributions
V.S. conceived the idea. V.S., C.H. and W.K. designed and conducted the experiments. A.R.D. and N.E. developed the theoretical description. A.R.D. performed the numerical simulations. C.H. and V.S. co-wrote the paper. W.K. supervised the project. All authors contributed to the discussion and data analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Shvedov, V., Davoyan, A., Hnatovsky, C. et al. A long-range polarization-controlled optical tractor beam. Nature Photon 8, 846–850 (2014). https://doi.org/10.1038/nphoton.2014.242
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2014.242
This article is cited by
-
Wavefront control of subcycle vortex pulses via carrier-envelope-phase tailoring
Light: Science & Applications (2023)
-
Ultrafast beam pattern modulation by superposition of chirped optical vortex pulses
Scientific Reports (2022)
-
Vectorial Doppler metrology
Nature Communications (2021)
-
Micro-scale opto-thermo-mechanical actuation in the dry adhesive regime
Light: Science & Applications (2021)
-
Metasurface optics for on-demand polarization transformations along the optical path
Nature Photonics (2021)