Abstract
Mode-locked lasers have enabled some of the most precise measurements ever performed, from attosecond time-domain spectroscopy to metrology with frequency combs. However, such extreme precision belies the complexity of the underlying mode-locking dynamics. This complexity is particularly evident in the emergence of the mode-locked state, an intrinsically singular, non-repetitive transition. Many details of mode-locking are well understood, yet conventional spectroscopy cannot resolve the nascent dynamics in passive mode-locking on their natural nanosecond timescale, the single pulse period. Here, we capture the pulse-resolved spectral evolution of a femtosecond pulse train from the initial fluctuations, recording ∼900,000 consecutive periods. We directly observe critical phenomena on timescales from tens to thousands of roundtrips, including the birth of the broadband spectrum, accompanying wavelength shifts and transient interference dynamics described as auxiliary-pulse mode-locking. Enabled by the time-stretch transform, the results may impact laser design, ultrafast diagnostics and nonlinear optics.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Haus, H. A. Mode-locking of lasers. IEEE J. Sel. Top. Quantum Electron. 6, 1173–1185 (2000).
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163 (2009).
Agrawal, G. P. Nonlinear Fiber Optics (Academic, 2007).
Dudley, J. M., Genty, G. & Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 78, 1135 (2006).
Solli, D., Ropers, C., Koonath, P. & Jalali, B. Optical rogue waves. Nature 450, 1054–1057 (2007).
Birkholz, S. et al. Spatiotemporal rogue events in optical multiple filamentation. Phys. Rev. Lett. 111, 243903 (2013).
Morgner, U. et al. Sub-two-cycle pulses from a Kerr-lens mode-locked Ti:sapphire laser. Opt. Lett. 24, 411–413 (1999).
Sutter, D. H. et al. Semiconductor saturable-absorber mirror-assisted Kerr-lens mode-locked Ti:sapphire laser producing pulses in the two-cycle regime. Opt. Lett. 24, 631–633 (1999).
Udem, T., Holzwarth, R. & Hänsch, T. W. Optical frequency metrology. Nature 416, 233–237 (2002).
Keller, U. Recent developments in compact ultrafast lasers. Nature 424, 831–838 (2003).
Spence, D. E., Kean, P. N. & Sibbett, W. 60-fsec pulse generation from a self-mode-locked Ti:sapphire laser. Opt. Lett. 16, 42–44 (1991).
Ippen, E. P., Haus, H. A. & Liu, L. Additive pulse mode locking. J. Opt. Soc. Am. B 6, 1736–1745 (1989).
Krausz, F., Brabec, T. & Spielmann, C. Self-starting passive mode locking. Opt. Lett. 16, 235–237 (1991).
Salin, F., Pich, M. & Squier, J. Mode locking of Ti:Al2O3 lasers and self-focusing: a Gaussian approximation. Opt. Lett. 16, 1674–1676 (1991).
Chilla, J. L. & Martinez, O. E. Spatial-temporal analysis of the self-mode-locked Ti:sapphire laser. J. Opt. Soc. Am. B 10, 638–643 (1993).
Ippen, E. P. Principles of passive mode locking. Appl. Phys. B 58, 159–170 (1994).
Krausz, F. et al. Femtosecond solid-state lasers. IEEE J. Quantum Electron. 28, 2097–2122 (1992).
Herrmann, J. Starting dynamic, self-starting condition and mode-locking threshold in passive, coupled-cavity or Kerr-lens mode-locked solid-state lasers. Opt. Commun. 98, 111–116 (1993).
Kartner, F. X., Jung, I. & Keller, U. Soliton mode-locking with saturable absorbers. IEEE J. Sel. Top. Quantum Electron. 2, 540–556 (1996).
Cerullo, G., De Silvestri, S. & Magni, V. Self-starting Kerr-lens mode locking of a Ti:sapphire laser. Opt. Lett. 19, 1040–1042 (1994).
Shieh, J.-M., Ganikhanov, F., Lin, K.-H., Hsieh, W.-F. & Pan, C.-L. Completely self-starting picosecond and femtosecond Kerr-lens mode-locked Ti:sapphire laser. J. Opt. Soc. Am. B 12, 945–949 (1995).
Solis, J. et al. Experimental study of a self-starting Kerr-lens mode-locked titanium-doped sapphire laser. Opt. Commun. 123, 547–552 (1996).
Kuo, J.-C. et al. Pulse-forming dynamics of a cw passively mode-locked Ti:sapphire/DDI laser. Opt. Lett. 17, 334–336 (1992).
Pu, N.-W., Shieh, J.-M., Lai, Y. & Pan, C.-L. Starting dynamics of a cw passively mode-locked picosecond Ti:sapphire/DDI laser. Opt. Lett. 20, 163–165 (1995).
Ozimek, F. et al. Witnessing the pulse birth—transient dynamics in a passively mode-locked femtosecond laser. Laser Phys. Lett. 10, 125003 (2013).
Sarukura, N. & Ishida, Y. Pulse evolution dynamics of a femtosecond passively mode-locked Ti: sapphire laser. Opt. Lett. 17, 61–63 (1992).
Wei, X., Zhang, C., Li, B. & Wong, K. K. Y. Observing the spectral dynamics of a mode-locked laser with ultrafast parametric spectro-temporal analyzer. Paper STh3L.4, CLEO 2015, OSA Technical Digest (Optical Society of America, 2015).
Kelkar, P., Coppinger, F., Bhushan, A. & Jalali, B. Time-domain optical sensing. Electron. Lett. 35, 1661–1662 (1999).
Solli, D., Gupta, S. & Jalali, B. Optical phase recovery in the dispersive Fourier transform. Appl. Phys. Lett. 95, 231108 (2009).
Bhushan, A., Coppinger, F. & Jalali, B. Time-stretched analogue-to-digital conversion. Electron. Lett. 34, 839–841 (1998).
Solli, D., Herink, G., Jalali, B. & Ropers, C. Fluctuations and correlations in modulation instability. Nature Photon. 6, 463–468 (2012).
Godin, T. et al. Real time noise and wavelength correlations in octave-spanning supercontinuum generation. Opt. Express 21, 18452–18460 (2013).
Descloux, D. et al. Spectrotemporal dynamics of a picosecond OPO based on chirped quasi-phase-matching. Opt. Lett. 40, 280–283 (2015).
Runge, A. F., Broderick, N. G. & Erkintalo, M. Observation of soliton explosions in a passively mode-locked fiber laser. Optica 2, 36–39 (2015).
Goda, K. et al. High-throughput single-microparticle imaging flow analyzer. Proc. Natl Acad. Sci. USA 109, 11630–11635 (2012).
Liu, Y.-M., Sun, K., Prucnal, P. R. & Lyon, S. Simple method to start and maintain self-mode-locking of a Ti:sapphire laser. Opt. Lett. 17, 1219–1221 (1992).
Herrmann, J. & Müller, M. Operating principle, saturable loss, and self-frequency shift in Kerr-shift mode-locked lasers. Opt. Lett. 20, 22–24 (1995).
Kalashnikov, V. L., Sorokin, E. & Sorokina, I. T. Mechanisms of spectral shift in ultrashort-pulse laser oscillators. J. Opt. Soc. Am. B 18, 1732–1741 (2001).
Gordon, A., Gat, O., Fischer, B. & Kärtner, F. X. Self-starting of passive mode locking. Opt. Express 14, 11142–11154 (2006).
Li, H., Ouzounov, D. G. & Wise, F. W. Starting dynamics of dissipative-soliton fiber laser. Opt. Lett. 35, 2403–2405 (2010).
Soto-Crespo, J., Akhmediev, N. & Town, G. Continuous-wave versus pulse regime in a passively mode-locked laser with a fast saturable absorber. J. Opt. Soc. Am. B 19, 234–242 (2002).
Vodonos, B. et al. Experimental study of the stochastic nature of the pulsation self-starting process in passive mode locking. Opt. Lett. 30, 2787–2789 (2005).
Menyuk, C. R. et al. Pulse dynamics in mode-locked lasers: relaxation oscillations and frequency pulling. Opt. Express 15, 6677–6689 (2007).
Antenucci, F., Berganza, M. I. & Leuzzi, L. Statistical physical theory of mode-locking laser generation with a frequency comb. Phys. Rev. A 91, 043811 (2015).
Spielmann, C., Krausz, F., Brabec, T., Wintner, E. & Schmidt, A. Experimental study of additive-pulse mode locking in an Nd:glass laser. IEEE J. Quantum Electron. 27, 1207–1213 (1991).
Haus, H. & Ippen, E. Self-starting of passively mode-locked lasers. Opt. Lett. 16, 1331–1333 (1991).
Komarov, A., Komarov, K. & Mitschke, F. Phase-modulation bistability and threshold self-start of laser passive mode locking. Phys. Rev. A 65, 053803 (2002).
Sun, Z. et al. Graphene mode-locked ultrafast laser. ACS Nano 4, 803–810 (2010).
Durfee, C. G. et al. Direct diode-pumped Kerr-lens mode-locked Ti: sapphire laser. Opt. Express 20, 13677–13683 (2012).
Huber, R., Wojtkowski, M. & Fujimoto, J. Fourier domain mode locking (FDML): a new laser operating regime and applications for optical coherence tomography. Opt. Express 14, 3225–3237 (2006).
Leonetti, M., Conti, C. & Lopez, C. The mode-locking transition of random lasers. Nature Photon. 5, 615–617 (2011).
Herr, T. et al. Temporal solitons in optical microresonators. Nature Photon. 8, 145–152 (2014).
Fard, A. M., Gupta, S. & Jalali, B. Photonic time-stretch digitizer and its extension to real-time spectroscopy and imaging. Laser Photon. Rev. 7, 207–263 (2013).
Acknowledgements
The UCLA work was supported by the Office of Naval Research (ONR) Multidisciplinary University Research (MURI) programme on Optical Computing and the ONR MURI programme on Nanophotonics.
Author information
Authors and Affiliations
Contributions
All authors were closely involved in this study and contributed to the ideas, realization of the experiments, data analysis and interpretation, and writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1914 kb)
Supplementary information
Supplementary Movie 1 (MP4 4164 kb)
Rights and permissions
About this article
Cite this article
Herink, G., Jalali, B., Ropers, C. et al. Resolving the build-up of femtosecond mode-locking with single-shot spectroscopy at 90 MHz frame rate. Nature Photon 10, 321–326 (2016). https://doi.org/10.1038/nphoton.2016.38
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2016.38
This article is cited by
-
Transient breathing dynamics during extinction of dissipative solitons in mode-locked fiber lasers
Frontiers of Optoelectronics (2024)
-
Radiation build-up and dissipation in Raman random fiber laser
Science China Information Sciences (2024)
-
Differential phase-diversity electrooptic modulator for cancellation of fiber dispersion and laser noise
Nature Communications (2023)
-
Heteronuclear multicolor soliton compounds induced by convex-concave phase in fiber lasers
Communications Physics (2023)
-
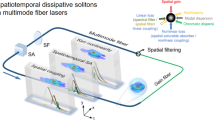
Spatiotemporal mode-locking and dissipative solitons in multimode fiber lasers
Light: Science & Applications (2023)