Abstract
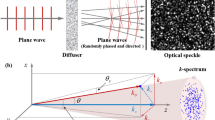
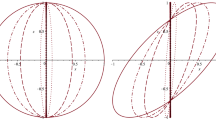
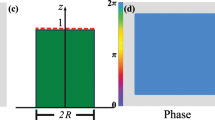
When Hanbury Brown and Twiss (HBT) proposed their technique of intensity correlation measurements1,2,3 to examine the angular size of stars in the visible range, they challenged the common conception of quantum mechanics and kicked off a discussion that led to the establishment of quantum optics4,5,6. In this Letter we revisit this fundamental technique and study its implications in the presence of space curvature. To this end we theoretically and experimentally investigate the evolution of speckle patterns propagating along two-dimensional surfaces of constant positive and negative Gaussian curvature, defying the notion that light always gains spatial coherence during free-space propagation. We also discuss the measurability of the traversed space's curvature utilizing HBT from an inhabitant's point of view. Through their symmetry, surfaces with constant Gaussian curvature act as analogue models for universes possessing non-vanishing cosmological constants.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Hanbury Brown, R. & Twiss, R. Q. Correlation between photons in two coherent beams of light. Nature 177, 27–29 (1956).
Hanbury Brown, R. & Twiss, R. Q. A test of a new type of interstellar interferometer on Sirius. Nature 178, 1046–1048 (1956).
Hanbury Brown, R., Davis, J. & Allen, L. R. The angular diameters of 32 stars. Mon. Not. R. Astron. Soc. 167, 121–136 (1974).
Purcell, E. M. The question of correlation between photons in coherent light rays. Nature 178, 1449–1450 (1956).
Glauber, R. J. Photon correlations. Phys. Rev. Lett. 10, 84–86 (1963).
Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766–2788 (1963).
Foellmi, C. Intensity interferometry and the second-order correlation function g(2) in astrophysics. Astron. Astrophys. 507, 1719–1727 (2009).
Malvimat, V., Wucknitz, O. & Saha, P. Intensity interferometry with more than two detectors? Mon. Not. R. Astron. Soc 437, 798–803 (2014).
Altman, E., Demler, E. & Lukin, M. D. Probing many-body states of ultracold atoms via noise correlations. Phys. Rev. A 70, 013603 (2004).
Schellekens, M. et al. Hanbury Brown Twiss effect for ultracold quantum gases. Science 310, 648–651 (2005).
Fölling, S. et al. Spatial quantum noise interferometry in expanding ultracold atom clouds. Nature 434, 481–484 (2005).
Perrin, A. et al. Hanbury Brown and Twiss correlations across the Bose-Einstein condensation threshold. Nature Phys. 8, 195–198 (2012).
Boal, D. H., Gelbke, C.-K. & Jennings, B. K. Intensity interferometry in subatomic physics. Rev. Mod. Phys. 62, 553–602 (1990).
Adams, J. et al. Azimuthally sensitive Hanbury Brown-Twiss interferometry in Au+Au collisions at . Phys. Rev. Lett. 93, 012301 (2004).
Müller, B., Schukraft, J. & Wyslouch, B. First results from Pb+Pb collisions at the LHC. Annu. Rev. Nucl. Part. Sci. 62, 361–386 (2012).
Bromberg, Y., Lahini, Y., Small, E. & Silberberg, Y. Hanbury Brown and Twiss interferometry with interacting photons. Nature Photon. 4, 721–726 (2010).
Batz, S. & Peschel, U. Linear and nonlinear optics in curved space. Phys. Rev. A 78, 043821 (2008).
Schultheiss, V. H. et al. Optics in curved space. Phys. Rev. Lett. 105, 143901 (2010).
Genov, D. A., Zhang, S. & Zhang, X. Mimicking celestial mechanics in metamaterials. Nature Phys. 5, 687–692 (2009).
Danner, A. J., Tyc, T. & Leonhardt, U. Controlling birefringence in dielectrics. Nature Photon. 5, 357–359 (2011).
Sheng, C., Liu, H., Wang, Y., Zhu, S. N. & Genov, D. A. Trapping light by mimicking gravitational lensing. Nature Photon. 7, 902–906 (2013).
Xu, L. & Chen, H. Conformal transformation optics. Nature Photon. 9, 15–23 (2015).
Saleh, B. E. A. & Teich, M. C. Fundamentals of Photonics (Wiley, 1991).
Foley, J. T. & Zubairy, M. S. The directionality of Gaussian Schell-model beams. Opt. Commun. 26, 297–300 (1978).
Friberg, A. T. & Sudol, R. J. Propagation parameters of Gaussian Schell-model beams. Opt. Commun. 41, 383–387 (1982).
Leonhardt, U. Perfect imaging without negative refraction. New J. Phys. 11, 093040 (2009).
Goodman, J. W. Statistical Optics (Wiley, 2000).
Lo, K. Y. Mega-masers and galaxies. Annu. Rev. Astron. Astrophys. 43, 625–676 (2005).
Reed, I. S. On a moment theorem for complex Gaussian processes. IRE Trans. Inform. Theor. 8, 194–195 (1962).
Picinbono, B. & Boileau, E. Higher-order coherence functions of optical fields and phase fluctuations. J. Opt. Soc. Am. 58, 784–789 (1968).
Acknowledgements
The authors would like to express their gratitude to R. Keding and P. Schrehardt at the glass workshop of the Max Planck Institute for the Science of Light (Erlangen) for their expertise in glass working. We are also grateful to T. Pertsch and F. Eilenberger from the University of Jena for providing a phase modulator. We gratefully acknowledge financial support by Deutsche Forschungsgemeinschaft (DFG) in the frame work of project PE 523/10-1 and the Cluster of Excellence Engineering of Advanced Materials (EAM).
Author information
Authors and Affiliations
Contributions
V.H.S. and S.B. derived the theory, V.H.S. and U.P. conceived and designed the experiments, V.H.S. performed the experiments and analysed the data, S.B. provided the MATLAB code for the simulations, V.H.S, S.B. and U.P. co-wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1195 kb)
Rights and permissions
About this article
Cite this article
Schultheiss, V., Batz, S. & Peschel, U. Hanbury Brown and Twiss measurements in curved space. Nature Photon 10, 106–110 (2016). https://doi.org/10.1038/nphoton.2015.244
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2015.244