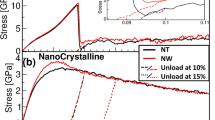
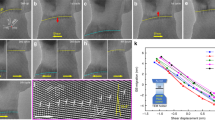
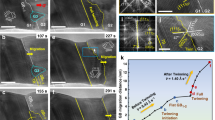
Abstract
Silicon crystals have an important role in the electronics industry, and silicon nanoparticles have applications in areas such as nanoelectromechanical systems, photonics and biotechnology1,2. However, the elastic–plastic transition observed in silicon is not fully understood; in particular, it is not known if the plasticity of silicon is determined by dislocations or by transformations between phases. Here, based on compression experiments and molecular dynamics simulations, we show that the mechanical properties of bulk silicon3,4,5,6 and silicon nanoparticles are significantly different. We find that bulk silicon exists in a state of relative constraint, with its plasticity dominated by phase transformations, whereas silicon nanoparticles are less constrained and display dislocation-driven plasticity. This transition, which we call deconfinement, can also explain the absence of phase transformations in deformed silicon nanowedges7,8. Furthermore, the phenomenon is in agreement with effects observed in shape-memory alloy nanopillars9, and provides insight into the origin of incipient plasticity10,11,12,13,14,15,16,17,18,19.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Ting, Z. & Li, J. Ultra-strength materials. Progr. Mater. Sci. 55, 710–757 (2010).
Craighead, H. G. Nanoelectromechanical systems. Science 290, 1532–1535 (2000).
Domnich, V., Gogotsi, Y. & Dub, S. Effect of phase transformations on the shape of the unloading curve in the nanoindentation of silicon. Appl. Phys. Lett. 76, 2214–2216 (2000).
Juliano, T., Domnich, V. & Gogotsi, Y. Examining pressure-induced phase transformations in silicon by spherical indentation and Raman spectroscopy: a statistical study. J. Mater. Res. 19, 3099–3108 (2004).
Chang, L. & Zhang, L. C. Deformation mechanisms at pop-out in monocrystalline silicon under nanoindentation. Acta Mater. 57, 2148–2153 (2009).
Bradby, J. E., Williams, J. S. & Swain, M. V. In situ electrical characterization of phase transformations in Si during indentation. Phys. Rev. B 67, 085205 (2003).
Minor, A. M. et al. Room temperature dislocation plasticity in silicon. Phil. Mag. 85, 323–330 (2005).
Ge, D., Minor, A. M., Stach, E. A. & Morris, J. W. Size effects in the nanoindentation of silicon at ambient temperature. Phil. Mag. 86, 4069–4080 (2006).
San Juan, J., No, M. L. & Schuh, C. A. Nanoscale shape-memory alloys for ultrahigh mechanical damping. Nature Nanotech. 4, 415–419 (2009).
Li, J., Van Vliet, K. J., Zhu, T., Yip, S. & Suresh, S. Atomistic mechanisms governing elastic limit and incipient plasticity in crystals. Nature 418, 307–310 (2002).
Szlufarska, I. Nakano, A. & Vashishta, P. A Crossover in the mechanical response of nanocrystalline ceramics. Science 309, 911–914 (2005).
Schuh, C. A. Mason, J. K. & Lund, A. C. Quantitative insight into dislocation nucleation from high-temperature nanoindentation experiments. Nature Mater. 4, 617–621 (2005).
Mason, J. K., Lund, A. C. & Schuh, C. A. Determining the activation energy and volume for the onset of plasticity during nanoindentation. Phys. Rev. B 73, 054102 (2006).
Gerberich, W. W. & Mook, W. M. Nanomechanics: a new picture of plasticity. Nature Mater. 4, 577–578 (2005).
Gerberich, W. W. et al. Superhard silicon nanospheres. J. Mech. Phys. Solids 51, 979–992 (2003).
Gerberich, W. W. et al. Reverse plasticity in single crystal silicon nanospheres. Int. J. Plast. 21, 2391–2405 (2005).
Chrobak, D., Nordlund, K. & Nowak, R. Nondislocation origin of GaAs nanoindentation pop-in event. Phys. Rev. Lett. 98, 045502 (2007).
Valentini, P., Gerberich, W. W. & Dumitrica, T. Phase-transition plasticity response in uniaxially compressed silicon nanospheres. Phys. Rev. Lett. 99, 175701 (2007).
Nowak, R. et al. An electric current spike linked to nanoscale plasticity. Nature Nanotech. 4, 287–291 (2009).
Nowak, R., Yoshida, F., Chrobak, D., Kurzydlowski, K. J., Takagi T. & Sasaki, T. in Encyclopedia of Nanoscience and Nanotechnology (ed. Nalwa, S. H.) 313–374 (American Scientific, 2010).
Stillinger, F. H. & Weber, T. A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 31, 5262–5271 (1985).
Godet, J., Pizzagalli, L., Brochard, S. & Beauchamp, P. Theoretical study of dislocation nucleation from simple surface defects in semiconductors. Phys. Rev. B 70, 054109 (2004).
Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 37, 6991–7000 (1988).
Bazant, M. Z., Kaxiras, E. & Justo, J. F. Environment-dependent interatomic potential for bulk silicon. Phys. Rev. B 56, 8542–8552 (1997).
Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Angew. Math. 92, 156–171 (1882).
Mo, Y., Turner, K. T. & Szlufarska, I. Friction laws at the nanoscale. Nature 457, 1116–1119 (2009).
Li, X., Ono, T. & Wang, Y. & Esashi, M. Ultrathin single crystalline silicon cantilever resonators: fabrication technology and significant specimen size effect on Young's modulus, Appl. Phys. Lett. 83, 3081–3083 (2003).
Zimmerman, J. A., Kelchner, C. L., Klein, P. A., Hamilton, J. C. & Foiles, S. M. Surface step effects on nanoindentation. Phys. Rev. Lett. 87, 165507 (2001).
Choi, Y., Van Vliet, K. J., Li, J. & Suresh, S. Size effects on the onset of plastic deformation during nanoindentation of thin films and patterned lines. J. Appl. Phys. 94, 6050–6058 (2003).
Wu, Y. Q. & Xu, Y. B. Lattice-distortion-induced amorphization in indented [110] silicon. J. Mater. Res. 14, 682–687 (1999).
Lorenz, D. et al. Pop-in effect as homogeneous nucleation of dislocations during nanoindentation. Phys. Rev. B 67, 172101 (2003).
Piltz, R. O. et al. Structure and properties of silicon XII: a complex tetrahedrally bonded phase. Phys. Rev. B 52, 4072–4085 (1995).
Rao, N. P. et al. Hypersonic plasma particle deposition of nanostructured silicon and silicon carbide. J. Aerosol Sci. 29, 707–720 (1998).
Acknowledgements
The authors gratefully acknowledge the CSC–IT Center for Science for computation resources and the Ceramic Society of Japan for invaluable assistance. R.N., D.C. and N.T. thank the Academy of Finland for partial support under the FINNANO programme and NANOSPIKE research project. A.B. and W.W.G. acknowledge the support of the National Science Foundation (NSF; CTS-0506748 and CMMI-00800896). R.N. acknowledges the involvement of the Research Foundation of Helsinki University of Technology, as well as the NANOINDENT EU-research grant. D.C. and R.N. thank R. Nieminen and K. Niihara for valuable discussions. The authors also thank A. Poludniak for careful reading of the manuscript and stimulating comments.
Author information
Authors and Affiliations
Contributions
D.C. carried out the calculations and analysed the compatibility of the theoretical and experimental data. R.N. conceived the concept of deconfinement-driven transition and designed the research project. N.T. analysed the data. W.W.G. designed and supervised the experimental part, and A.B. and O.U. performed nanocompression tests and analysed the output. R.N. and D.C. wrote the paper. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1484 kb)
Supplementary information
Supplementary movie 1 (AVI 2636 kb)
Supplementary information
Supplementary movie 2 (AVI 3534 kb)
Rights and permissions
About this article
Cite this article
Chrobak, D., Tymiak, N., Beaber, A. et al. Deconfinement leads to changes in the nanoscale plasticity of silicon. Nature Nanotech 6, 480–484 (2011). https://doi.org/10.1038/nnano.2011.118
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nnano.2011.118
This article is cited by
-
Plasticity in diamond nanoparticles: dislocations and amorphization during loading and dislocation multiplication during unloading
Journal of Materials Science (2023)
-
Mechanical behavior of surface-patterned and coated Si or Ge wafers for superhydrophobic and antireflective light transmitting windows
Journal of Materials Science (2022)
-
Mechanical properties, phase transitions, and fragmentation mechanisms of 6H, 3C, and amorphous SiC nanoparticles under compression
Applied Physics A (2021)
-
Molecular Dynamics Study on Tip-Based Nanomachining: A Review
Nanoscale Research Letters (2020)
-
Numerical study of three-body diamond abrasive nanoindentation of single-crystal Si by molecular dynamics simulation
Applied Physics A (2019)