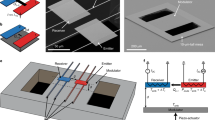
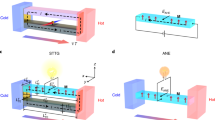
Abstract
Rectification of thermal fluctuations in mesoscopic conductors is the key idea behind recent attempts to build nanoscale thermoelectric energy harvesters to convert heat into useful electric power1,2,3. So far, most concepts have made use of the Seebeck effect in a two-terminal geometry4,5,6,7,8, where heat and charge are both carried by the same particles. Here, we experimentally demonstrate the working principle of a new kind of energy harvester, proposed recently9, using two capacitively coupled quantum dots. We show that, due to the novel three-terminal design of our device, which spatially separates the heat reservoir from the conductor circuit, the directions of charge and heat flow become decoupled. This enables us to manipulate the direction of the generated charge current by means of external gate voltages while leaving the direction of heat flow unaffected. Our results pave the way for a new generation of multi-terminal nanoscale heat engines.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
White, B. E. Beyond the battery. Nature Nanotech. 3, 71–72 (2008).
Mahan, G. D. & Sofo, J. O. The best thermoelectric. Proc. Natl Acad. Sci. USA 93, 7436–7439 (1996).
Radousky, H. B. & Liang, H. Energy harvesting: an integrated view of materials, devices and applications. Nanotechnology 23, 502001 (2012).
Shakouri, A. Recent developments in semiconductor thermoelectric physics and materials. Annu. Rev. Mater. Res. 41, 399–431 (2011).
Humphrey, T. & Linke, H. Reversible thermoelectric nanomaterials. Phys. Rev. Lett. 94, 096601 (2005).
Hicks, L. & Dresselhaus, M. S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 47, 12727–12731 (1993).
Whitney, R. S. Nonlinear thermoelectricity in point contacts at pinch off: a catastrophe aids cooling. Phys. Rev. B 88, 064302 (2013).
Juergens, S., Haupt, F., Moskalets, M. & Splettstoesser, J. Thermoelectric performance of a driven double quantum dot. Phys. Rev. B 87, 245423 (2013).
Sánchez, R. & Büttiker, M. Optimal energy quanta to current conversion. Phys. Rev. B. 83, 085428 (2011).
Cutler, M. & Mott, N. F. Observation of Anderson localization in an electron gas. Phys. Rev. 181, 1336–1340 (1969).
Sivan, U. & Imry, Y. Multichannel Landauer formula for thermoelectric transport with application to thermopower near the mobility edge. Phys. Rev. B 33, 551–558 (1986).
Beenakker, C. W. J. & Staring, A. A. M. Theory of the thermopower of a quantum dot. Phys. Rev. B 46, 9667–9676 (1992).
Molenkamp, L. W., Van Houten, H., Beenakker, C. W. J., Eppenga, R. & Foxon, C. T. Quantum oscillations in the transverse voltage of a channel in the nonlinear transport regime. Phys. Rev. Lett. 65, 1052 (1990).
Entin-Wohlman, O., Imry, Y. & Aharony, A. Three-terminal thermoelectric transport through a molecular junction. Phys. Rev. B 82, 115314 (2010).
Sánchez, D. & Serra, L. Thermoelectric transport of mesoscopic conductors coupled to voltage and thermal probes. Phys. Rev. B 84, 201307(R) (2011).
Jiang, J.-H., Entin-Wohlman, O. & Imry, Y. Thermoelectric three-terminal hopping transport through one-dimensional nanosystems. Phys. Rev. B 85, 075412 (2012).
Sothmann, B., Sánchez, R., Jordan, A. N. & Büttiker, M. Rectification of thermal fluctuations in a chaotic cavity heat engine. Phys. Rev. B 85, 205301 (2012).
Jordan, A. N., Sothmann, B., Sánchez, R. & Büttiker, M. Powerful and efficient energy harvester with resonant-tunneling quantum dots. Phys. Rev. B 87, 075312 (2013).
Bergenfeldt, C., Samuelsson, P., Sothmann, B., Flindt, C. & Büttiker, M. Hybrid microwave-cavity heat engine. Phys. Rev. Lett. 112, 076803 (2014).
Brandner, K., Saito, K. & Seifert, U. Strong bounds on Onsager coefficients and efficiency for three-terminal thermoelectric transport in a magnetic field. Phys. Rev. Lett. 110, 070603 (2013).
Molenkamp, L. W., Flensberg, K. & Kemerink, M. Scaling of the Coulomb energy due to quantum fluctuations in the charge on a quantum dot. Phys. Rev. Lett. 75, 4282 (1995).
MacLean, K. et al. Energy-dependent tunneling in a quantum dot. Phys. Rev. Lett. 98, 036802 (2007).
Van der Wiel, W. G. et al. Electron transport through double quantum dots. Rev. Mod. Phys. 75, 1–22 (2002).
Thierschmann, H. et al. Thermal gating of charge currents with Coulomb coupled quantum dots. Preprint at http://arXiv/abs/1502.03021 (2015).
Appleyard, N. J., Nicholls, J. T., Simmons, M. Y., Tribe, W. R. & Pepper, M. Thermometer for the 2D electron gas using 1D thermopower. Phys. Rev. Lett. 81, 3491 (1998).
Acknowledgements
The authors thank M. Büttiker for drawing our attention to the subject. The authors also thank C. Thienel for discussions and L. Maier for help with device fabrication. This work was supported by the Deutsche Forschungsgemeinschaft via SPP1386, the Swiss National Science Foundation, the Spanish MICINN Juan de la Cierva programme and MAT2014-58241-P, COST Action MP1209.
Author information
Authors and Affiliations
Contributions
H.T., H.B. and L.W.M. designed the experiment. C.H. and W.H. provided the wafer material. F.A. fabricated the sample. H.T. and F.A. conducted the measurements. R.S. and B.S. performed the model calculations. All authors discussed the results. H.T., B.S., R.S., H.B. and L.W.M. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 485 kb)
Rights and permissions
About this article
Cite this article
Thierschmann, H., Sánchez, R., Sothmann, B. et al. Three-terminal energy harvester with coupled quantum dots. Nature Nanotech 10, 854–858 (2015). https://doi.org/10.1038/nnano.2015.176
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nnano.2015.176
This article is cited by
-
Scalable fabrication of graphene nanoribbon quantum dot devices with stable orbital-level spacing
Communications Materials (2022)
-
Non-local triple quantum dot thermometer based on Coulomb-coupled systems
Scientific Reports (2022)
-
Thermoelectric Effect in a Correlated Quantum Dot Side-Coupled to Majorana Bound States
Nanoscale Research Letters (2020)
-
Electric field control of radiative heat transfer in a superconducting circuit
Nature Communications (2020)
-
Optical shaping of the polarization anisotropy in a laterally coupled quantum dot dimer
Light: Science & Applications (2020)