Abstract
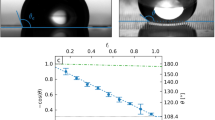
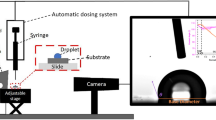
Controlling surface wettability and liquid spreading on patterned surfaces is of significant interest for a broad range of applications, including DNA microarrays, digital lab-on-a-chip, anti-fogging and fog-harvesting, inkjet printing and thin-film lubrication1,2,3,4,5,6,7,8. Advancements in surface engineering, with the fabrication of various micro/nanoscale topographic features9,10,11,12,13, and selective chemical patterning on surfaces14,15, have enhanced surface wettability3,16,17 and enabled control of the liquid film thickness18 and final wetted shape19. In addition, groove geometries and patterned surface chemistries have produced anisotropic wetting, where contact-angle variations in different directions resulted in elongated droplet shapes20,21,22,23,24,25,26. In all of these studies, however, the wetting behaviour preserves left–right symmetry. Here, we demonstrate that we can harness the design of asymmetric nanostructured surfaces to achieve uni-directional liquid spreading, where the liquid propagates in a single preferred direction and pins in all others. Through experiments and modelling, we determined that the spreading characteristic is dependent on the degree of nanostructure asymmetry, the height-to-spacing ratio of the nanostructures and the intrinsic contact angle. The theory, based on an energy argument, provides excellent agreement with experimental data. The insights gained from this work offer new opportunities to tailor advanced nanostructures to achieve active control of complex flow patterns and wetting on demand.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Chiou, N.-R., Lu, C., Guan, J., Lee, L. J. & Epstein, A. J. Growth and alignment of polyaniline nanofibres with superhydrophobic, superhydrophilic and other properties. Nature Nanotech. 2, 354–357 (2007).
Krupenkin, T. N., Taylor, J. A., Schneider, T. M. & Yang, S. From rolling ball to complete wetting: The dynamic tuning of liquid on nanostructured surfaces. Langmuir 20, 3824–3827 (2004).
Wang, R. et al. Light-induced amphiphilic surfaces. Nature 388, 431–432 (1997).
Cebeci, F. Ç., Wu, Z., Zhai, L., Cohen, R. E. & Rubner, M. F. Nanoporosity-driven superhydrophilicity: A means to create multifunctional antifogging coatings. Langmuir 22, 2856–2862 (2006).
Garrod, R. P. et al. Mimicking a stenocara beetle’s back for microcondensation using plasmachemical patterned superhydrophobic–superhydrophilic surfaces. Langmuir 23, 689–693 (2007).
Wang, J. Z., Zheng, Z. H., Li, H. W., Huck, W. T. S. & Sirringhaus, H. Dewetting of conducting polymer inkjet droplets on patterned surfaces. Nature Mater. 3, 171–176 (2004).
Hiratsuka, K., Bohno, A. & Endo, H. Water droplet lubrication between hydrophilic and hydrophobic surfaces. J. Phys. Conf. Ser. 89, 012012 (2007).
Extrand, C. W., Moon, S. I., Hall, P. & Schmidt, D. Superwetting of structured surfaces. Langmuir 23, 8882–8890 (2007).
Quéré, D. Non-sticking drops. Rep. Prog. Phys. 68, 2495–2532 (2005).
Őner, D. & McCarthy, T. J. Ultrahydrophobic surfaces. Effects of topography length scales on wettability. Langmuir 16, 7777–7782 (2000).
Bico, J., Tordeux, C. & Quéré, D. Rough wetting. Europhys. Lett. 55, 214–220 (1999).
Seemann, R., Brinkmann, M., Kramer, E. J., Lange, F. F. & Lipowsky, R. Wetting morphologies at microstructured surfaces. Proc. Natl Acad. Sci. USA 102, 1848–1852 (2005).
Maritines, E. et al. Superhydrophobicity and super hydrophilicity of regular nanopatterns. Nano Lett. 5, 2097–2130 (2005).
Dupuis, A., Léopoldès, J., Bucknall, D. G. & Yeomans, J. M. Control of drop positioning using chemical patterning. Appl. Phys. Lett. 87, 024103 (2005).
Gleiche, M., Chi, L. F. & Fuchs, H. Nanoscopic channel lattices with controlled anisotropic wetting. Nature 403, 173–175 (2000).
Wenzel, R. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 28, 988–994 (1936).
Vorobyev, A. Y. & Guo, C. Metal pumps liquid uphill. Appl. Phys. Lett. 94, 224102 (2009).
Xiao, R., Chu, K.-H. & Wang, E. N. Multi-layer liquid spreading on superhydrophilic nanostructured surfaces. Appl. Phys. Lett. 94, 193104 (2009).
Courbin, L. et al. Imbibition by polygonal spreading on microdecorated surfaces. Nature Mater. 6, 661–664 (2007).
Zhang, F. & Low, H. Y. Anisotropic wettability on imprinted hierarchical structures. Langmuir 23, 7793–7798 (2007).
Bico, J., Marzolin, C. & Quéré, D. Pearl drops. Europhys. Lett. 47, 220–226 (1999).
Chen, Y., He, B., Lee, J. & Patankar, N. A. Anisotropy in the wetting of rough surfaces. J. Colloid Interface Sci. 281, 458–464 (2005).
Chung, J. Y., Youngblood, J. P. & Stafford, C. M. Anisotropic wetting on tunable micro-wrinkled surfaces. Soft Matter. 3, 1163–1169 (2007).
Kusumaatmaja, H., Vrancken, R. J., Bastiaansen, C. W. M. & Yeomans, J. M. Anisotropic drop morphologies on corrugated surfaces. Langmuir 24, 7299–7308 (2008).
Drelich, J., Wilbur, J. L., Miller, J. D. & Whitesides, G. M. Contact angles for liquid drops at a model heterogeneous surface consisting of alternating and parallel hydrophobic/hydrophilic strips. Langmuir 12, 1913–1922 (1996).
Gau, H., Herminghaus, S., Lenz, P. & Lipowsky, R. Liquid morphologies on structured surfaces: From microchannels to microchips. Science 283, 46–49 (1999).
Tenhaeff, W. E. & Gleason, K. K. Initiated and oxidative chemical vapour deposition of polymeric thin films: iCVD and oCVD. Adv. Funct. Mater. 18, 979–992 (2008).
Baxamusa, S. H., Im, S. G. & Gleason, K. K. Initiated and oxidative chemical vapour deposition: A scalable method for conformal and functional polymer films on real substrates. Phys. Chem. Chem. Phys. 11, 5227–5240 (2009).
Alf, M. E. et al. Chemical vapor deposition (CVD) of conformal, functional, and responsive polymer films. Adv. Mater. 21, 1–35 (2009).
Acknowledgements
The authors gratefully acknowledge financial support from the National Science Foundation (under Award EEC-0824328), the DARPA Young Faculty Award and the Northrop Grumman New Faculty Innovation Grant. The authors would also like to acknowledge the Intel Higher Education Grant for a generous computer donation, and the MIT Microsystems Technology Lab. The authors thank B. E. Polat from D. Blankschtein’s group for help with surface tension measurements, and especially, M. E. Alf and S. Baxamusa from K. K. Gleason’s group for the initiated chemical vapour polymer deposition, all in the Department of Chemical Engineering, MIT.
Author information
Authors and Affiliations
Contributions
All authors contributed to designing and conducting the experiments, model development and preparing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 528 kb)
Supplementary Information
Supplementary Movie 1 (MOV 2072 kb)
Supplementary Infromation
Supplementary Movie 2 (MOV 2861 kb)
Supplementary Information
Supplementary Movie 3 (MOV 2732 kb)
Rights and permissions
About this article
Cite this article
Chu, KH., Xiao, R. & Wang, E. Uni-directional liquid spreading on asymmetric nanostructured surfaces. Nature Mater 9, 413–417 (2010). https://doi.org/10.1038/nmat2726
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat2726
This article is cited by
-
Flexible hemline-shaped microfibers for liquid transport
Nature Chemical Engineering (2024)
-
Tesla valves and capillary structures-activated thermal regulator
Nature Communications (2023)
-
Autonomous and directional flow of water and transport of particles across a subliming dynamic crystal surface
Nature Chemistry (2023)
-
Scalable and switchable CO2-responsive membranes with high wettability for separation of various oil/water systems
Nature Communications (2023)
-
Scaling of Anisotropic Wetting Behavior of Water Drop Configuration Arising from Parallel Groove-Textured Stainless Steel Surfaces
Journal of Bio- and Tribo-Corrosion (2023)