Abstract
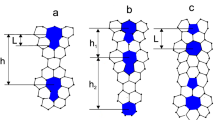
Most materials in available macroscopic quantities are polycrystalline. Graphene, a recently discovered two-dimensional form of carbon with strong potential for replacing silicon in future electronics1,2,3, is no exception. There is growing evidence of the polycrystalline nature of graphene samples obtained using various techniques4,5,6,7,8,9,10,11,12,13. Grain boundaries, intrinsic topological defects of polycrystalline materials14, are expected to markedly alter the electronic transport in graphene. Here, we develop a theory of charge carrier transmission through grain boundaries composed of a periodic array of dislocations in graphene based on the momentum conservation principle. Depending on the grain-boundary structure we find two distinct transport behaviours—either high transparency, or perfect reflection of charge carriers over remarkably large energy ranges. First-principles quantum transport calculations are used to verify and further investigate this striking behaviour. Our study sheds light on the transport properties of large-area graphene samples. Furthermore, purposeful engineering of periodic grain boundaries with tunable transport gaps would allow for controlling charge currents without the need to introduce bulk bandgaps in otherwise semimetallic graphene. The proposed approach can be regarded as a means towards building practical graphene electronics.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nature Mater. 6, 183–191 (2007).
Katsnelson, M. I. Graphene: Carbon in two dimensions. Mater. Today 10, 20–27 (2007).
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).
Albrecht, T. R., Mizes, H. A., Nogami, J., Park, S-i. & Quate, C. F. Observation of tilt boundaries in graphite by scanning tunneling microscopy and associated multiple tip effects. Appl. Phys. Lett. 52, 362–364 (1988).
Clemmer, C. R. & Beebe, T. P. Jr Graphite: A mimic for DNA and other biomolecules in scanning tunneling microscope studies. Science 251, 640–642 (1991).
Heckl, W. M. & Binnig, G. Domain walls on graphite mimic DNA. Ultramicroscopy 42, 1073–1078 (1992).
C˘ervenka, J. & Flipse, C. F. J. Structural and electronic properties of grain boundaries in graphite: Planes of periodically distributed point defects. Phys. Rev. B 79, 195429 (2009).
C˘ervenka, J., Katsnelson, M. I. & Flipse, C. F. J. Room-temperature ferromagnetism in graphite driven by two-dimensional networks of point defects. Nature Phys. 5, 840–844 (2009).
Coraux, J. et al. Growth of graphene on Ir(111). New J. Phys. 11, 023006 (2009).
Miller, D. L. et al. Observing the quantization of zero mass carriers in graphene. Science 324, 924–927 (2009).
Loginova, E., Nie, S., Thurmer, K., Bartelt, N. C. & McCarty, K. F. Defects of graphene on Ir(111): Rotational domains and ridges. Phys. Rev. B 80, 085430 (2009).
Park, H. J., Meyer, J., Roth, S. & Skákalová, V. Growth and properties of few-layer graphene prepared by chemical vapor deposition. Carbon 48, 1088–1094 (2010).
Lahiri, J., Lin, Y., Bozkurt, P., Oleynik, I. I. & Batzill, M. An extended defect in graphene as a metallic wire. Nature Nanotech. 5, 326–329 (2010).
Sutton, A. P. & Balluffi, R. W. Interfaces in Crystalline Materials (Clarendon Press, 1995).
Read, W. T. & Shockley, W. Dislocation models of crystal grain boundaries. Phys. Rev. 78, 275–289 (1950).
Yazyev, O. V. & Louie, S. G. Topological defects in graphene: Dislocations and grain boundaries. Phys. Rev. B 81, 195420 (2010).
White, C. T. & Mintmire, J. W. Density of states reflects diameter in nanotubes. Nature 394, 29–30 (1998).
Mintmire, J. W. & White, C. T. Universal density of states for carbon nanotubes. Phys. Rev. Lett. 81, 2506–2509 (1998).
Carraro, C. & Nelson, D. R. Grain-boundary buckling and spin-glass models of disorder in membranes. Phys. Rev. E 48, 3082–3090 (1993).
Simonis, P. et al. STM study of a grain boundary in graphite. Surf. Sci. 511, 319–322 (2002).
Liu, Y. & Yakobson, B. I. Cones, pringles, and grain boundary landscapes in graphene topology. Nano Lett. 10, 2178–2183 (2010).
Koskinen, P., Malola, S. & Häkkinen, H. Self-passivating edge reconstructions of graphene. Phys. Rev. Lett. 101, 115502 (2008).
Katsnelson, M. I., Novoselov, K. S. & Geim, A. K. Chiral tunnelling and the Klein paradox in graphene. Nature Phys. 2, 620–625 (2006).
Young, A. F. & Kim, P. Quantum interference and Klein tunnelling in graphene heterojunctions. Nature Phys. 5, 222–226 (2009).
Stander, N., Huard, B. & Goldhaber-Gordon, D. Evidence for Klein tunneling in graphene p–n junctions. Phys. Rev. Lett. 102, 026807 (2009).
Xia, F., Farmer, D. B., Lin, Y-M. & Avouris, P. Graphene field-effect transistors with high on/off current ratio and large transport band gap at room temperature. Nano Lett. 10, 715–718 (2010).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 14, 2745–2779 (2002).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Troullier, N. & Martins, J. L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 43, 1993–2006 (1991).
Brandbyge, M., Mozos, J-L., Ordejón, P., Taylor, J. & Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65, 165401 (2002).
Acknowledgements
We are grateful to J. J. Palacios, C-H. Park and D. Strubbe for their comments. This work was supported by National Science Foundation Grant No. DMR07-05941 and by the Director, Office of Science, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering Division, US Department of Energy under Contract No. DE-AC02-05CH11231. The structural parameters were determined using theoretical techniques and computer codes supported by NSF and the electronic transport calculations were carried out under the auspices of BES support. O.V.Y. acknowledges financial support of the Swiss National Science Foundation (grant no. PBELP2-123086). Computational resources have been provided by NSF through TeraGrid resources at NICS (Kraken) and by DOE at Lawrence Berkeley National Laboratory’s NERSC facility.
Author information
Authors and Affiliations
Contributions
O.V.Y. proposed the project, carried out derivation, computations and analyses and wrote the manuscript. S.G.L. directed the research, proposed analyses, interpreted results and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 340 kb)
Rights and permissions
About this article
Cite this article
Yazyev, O., Louie, S. Electronic transport in polycrystalline graphene. Nature Mater 9, 806–809 (2010). https://doi.org/10.1038/nmat2830
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat2830
This article is cited by
-
Electronic transport in graphene with out-of-plane disorder
npj 2D Materials and Applications (2024)
-
Effect of Line Defects on the Band Structures, Local Density of States, and the Landau Levels for Armchair Graphene Nanoribbons in the Quantum Hall Effect Regime
Journal of Electronic Materials (2024)
-
A second wave of topological phenomena in photonics and acoustics
Nature (2023)
-
An all 2D bio-inspired gustatory circuit for mimicking physiology and psychology of feeding behavior
Nature Communications (2023)
-
Novel nanostructures suspended in graphene vacancies, edges and holes
Science China Materials (2023)