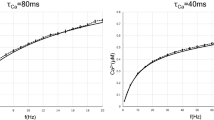
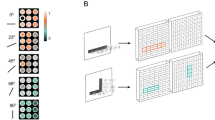
Abstract
Electrophysiological connectivity patterns in cortex often have a few strong connections, which are sometimes bidirectional, among a lot of weak connections. To explain these connectivity patterns, we created a model of spike timing–dependent plasticity (STDP) in which synaptic changes depend on presynaptic spike arrival and the postsynaptic membrane potential, filtered with two different time constants. Our model describes several nonlinear effects that are observed in STDP experiments, as well as the voltage dependence of plasticity. We found that, in a simulated recurrent network of spiking neurons, our plasticity rule led not only to development of localized receptive fields but also to connectivity patterns that reflect the neural code. For temporal coding procedures with spatio-temporal input correlations, strong connections were predominantly unidirectional, whereas they were bidirectional under rate-coded input with spatial correlations only. Thus, variable connectivity patterns in the brain could reflect different coding principles across brain areas; moreover, our simulations suggested that plasticity is fast.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout







Similar content being viewed by others
References
Buonomano, D.V. & Merzenich, M.M. Cortical plasticity: from synapses to maps. Annu. Rev. Neurosci. 21, 149–186 (1998).
Dan, Y. & Poo, M. Spike timing–dependent plasticity of neural circuits. Neuron 44, 23–30 (2004).
Song, S., Sjöström, P.J., Reigl, M., Nelson, S. & Chklovskii, D.B. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3, e350 (2005).
Lefort, S., Tomm, C., Sarria, J.C.F. & Petersen, C.C.H. The excitatory neuronal network of the C2 barrel column in mouse primary somatosensory cortex. Neuron 61, 301–316 (2009).
Yuste, R. & Bonhoeffer, T. Genesis of dendritic spines: insights from ultrastructural and imaging studies. Nat. Rev. Neurosci. 5, 24–34 (2004).
Hebb, D.O. The Organization of Behavior (Wiley, New York, 1949).
Malenka, R.C. & Bear, M.F. LTP and LTD: an embarassment of riches. Neuron 44, 5–21 (2004).
Markram, H., Lübke, J., Frotscher, M. & Sakmann, B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215 (1997).
Artola, A., Bröcher, S. & Singer, W. Different voltage-dependent thresholds for inducing long-term depression and long-term potentiation in slices of rat visual cortex. Nature 347, 69–72 (1990).
Ngezahayo, A., Schachner, M. & Artola, A. Synaptic activity modulates the induction of bidirectional synaptic changes in adult mouse hippocampus. J. Neurosci. 20, 2451–2458 (2000).
Dudek, S.M. & Bear, M.F. Bidirectional long-term modification of synaptic effectiveness in the adult and immature hippocampus. J. Neurosci. 13, 2910–2918 (1993).
Gerstner, W., Kempter, R., Van Hemmen, L. & Wagner, H. A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–81 (1996).
Legenstein, R., Naeger, C. & Maass, W. What can a neuron learn with spike timing–dependent plasticity? Neural Comput. 17, 2337–2382 (2005).
Gerstner, W. & Kistler, W.M. Spiking Neuron Models (Cambridge University Press, New York, 2002).
Lisman, J. & Spruston, N. Postsynaptic depolarization requirements for LTP and LTD: a critique of spike timing-dependent plasticity. Nat. Neurosci. 8, 839–841 (2005).
Sjöström, P.J., Turrigiano, G.G. & Nelson, S.B. Rate, timing and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164 (2001).
Shouval, H.Z., Bear, M.F. & Cooper, L.N. A unified model of NMDA receptor dependent bidirectional synaptic plasticity. Proc. Natl. Acad. Sci. USA 99, 10831–10836 (2002).
Lisman, J.E. & Zhabotinsky, A.M. A model of synaptic memory: a CaMKII/PP1 switch that potentiates transmission by organizing an AMPA receptor anchoring assembly. Neuron 31, 191–201 (2001).
Song, S. & Abbott, L.F. Cortical development and remapping through spike timing–dependent plasticity. Neuron 32, 339–350 (2001).
Lubenov, E.V. & Siapas, A.G. Decoupling through synchrony in neuronal circuits with propagation delays. Neuron 58, 118–131 (2008).
Levy, N., Horn, D., Meilijson, I. & Ruppin, E. Distributed synchrony in a cell assembly of spiking neurons. Neural Netw. 14, 815–824 (2001).
Morrison, A., Aertsen, A. & Diesmann, M. Spike timing–dependent plasticity in balanced random networks. Neural Comput. 19, 1437–1467 (2007).
Izhikevich, E.M. & Edelman, G.M. Large-scale model of mammalian thalamocortical systems. Proc. Natl. Acad. Sci. USA 105, 3593–3598 (2008).
Cooper, L.N., Intrator, N., Blais, B.S. & Shouval, H.Z. Theory of Cortical Plasticity (World Scientific, Singapore, 2004).
Miller, K.D. A model for the development of simple cell receptive fields and the ordered arrangement of orientation columns through activity dependent competition between ON- and OFF-center inputs. J. Neurosci. 14, 409–441 (1994).
Senn, W., Tsodyks, M. & Markram, H. An algorithm for modifying neurotransmitter release probability based on pre- and postsynaptic spike timing. Neural Comput. 13, 35–67 (2001).
Pfister, J.-P. & Gerstner, W. Triplets of spikes in a model of spike timing–dependent plasticity. J. Neurosci. 26, 9673–9682 (2006).
O'Connor, D.H., Wittenberg, G.M. & Wang, S.S.H. Dissection of bidirectional synaptic plasticity into saturable unidirectional processes. J. Neurophysiol. 94, 1565–1573 (2005).
Turrigiano, G.G. & Nelson, S.B. Homeostatic plasticity in the developing nervous system. Nat. Rev. Neurosci. 5, 97–107 (2004).
Nevian, T. & Sakmann, B. Spine Ca2+ signaling in spike timing–dependent plasticity. J. Neurosci. 26, 11001–11013 (2006).
Kampa, B.M., Letzkus, J.J. & Stuart, G.J. Requirement of dendritic calcium spikes for induction of spike timing–dependent synaptic plasticity. J. Physiol. (Lond.) 574, 283–290 (2006).
Kozloski, J. & Cecchi, G.A. Topological effects of synaptic spike timing–dependent plasticity. Preprint at <http://arxiv.org/abs/0810.0029> (2008).
Jadhav, S.P., Wolfe, J. & Feldman, D.E. Sparse temporal coding of elementary tactile features during active whisker sensation. Nat. Neurosci. (2009).
Blais, B.S., Intrator, N., Shouval, H. & Cooper, L. Receptive field formation in natural scene environments. Comparison of single-cell learning rules. Neural Comput. 10, 1797–1813 (1998).
Olshausen, B.A. & Field, D.J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 381, 607–609 (1996).
Hyvärinen, A., Karhunen, J. & Oja, E. Independent Component Analysis (Wiley, New York, 2001).
Oja, E. A simplified neuron as a principal component analyzer. J. Math. Biol. 15, 267–273 (1982).
Wang, H.X., Gerkin, R.C., Nauen, D.W. & Bi, G.-Q. Coactivation and timing-dependent integration of synaptic potentiation and depression. Nat. Neurosci. 8, 187–193 (2005).
Saudargiene, A., Porr, B. & Wörgötter, F. How the shape of pre- and postsynaptic signals can influence STDP: a biophysical model. Neural Comput. 16, 595–626 (2004).
Brader, J.M., Senn, W. & Fusi, S. Learning real-world stimuli in a neural network with spike-driven synaptic dynamics. Neural Comput. 19, 2881–2912 (2007).
Clopath, C., Ziegler, L., Vasilaki, E., Büsing, L. & Gerstner, W. Tag-trigger consolidation: a model of early and late long-term potentiation and depression. PLOS Comput. Biol. 4, e1000248 (2008).
Sjöström, P.J., Turrigiano, G.G. & Nelson, S.B. Neocortical LTD via coincident activation of presynaptic NMDA and cannabinoid receptors. Neuron 39, 641–654 (2003).
Sjöström, P.J. & Häusser, M. A cooperative switch determines the sign of synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron 51, 227–238 (2006).
Tsodyks, M.V. & Markram, H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc. Natl. Acad. Sci. USA 94, 719–723 (1997).
Frey, U. & Morris, R.G.M. Synaptic tagging and long-term potentiation. Nature 385, 533–536 (1997).
Remy, S. & Spruston, N. Dendritic spikes induce single-burst long-term potentiation. PNAS 104, 17192–17197 (2007).
Hardie, J. & Spruston, N. Synaptic depolarization is more effective than back-propagating action potentials during induction of associative long-term potentiation in hippocampal pyramidal neurons. J. Neurosci. 29, 3233–3241 (2009).
Golding, N.L., Staff, N.P. & Spruston, N. Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature 418, 326–331 (2002).
Brette, R. & Gerstner, W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94, 3637–3642 (2005).
Badel, L. et al. Dynamic I-V curves are reliable predictors of naturalistic pyramidal-neuron voltage traces. J. Neurophysiol. 99, 656–666 (2008).
Acknowledgements
This work was supported by the European project FACETS and the Swiss National Science Foundation.
Author information
Authors and Affiliations
Contributions
C.C. developed the model and carried out the experiments. L.B. and E.V. participated in discussions. W.G. supervised the project and wrote most of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–3 and Supplementary Methods (PDF 803 kb)
Rights and permissions
About this article
Cite this article
Clopath, C., Büsing, L., Vasilaki, E. et al. Connectivity reflects coding: a model of voltage-based STDP with homeostasis. Nat Neurosci 13, 344–352 (2010). https://doi.org/10.1038/nn.2479
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nn.2479
This article is cited by
-
A voltage-based Event-Timing-Dependent Plasticity rule accounts for LTP subthreshold and suprathreshold for dendritic spikes in CA1 pyramidal neurons
Journal of Computational Neuroscience (2024)
-
Dendrites help mitigate the plasticity-stability dilemma
Scientific Reports (2023)
-
Long- and short-term history effects in a spiking network model of statistical learning
Scientific Reports (2023)
-
Closing the loop between brain and electrical stimulation: towards precision neuromodulation treatments
Translational Psychiatry (2023)
-
The combination of Hebbian and predictive plasticity learns invariant object representations in deep sensory networks
Nature Neuroscience (2023)