Introduction

Numerous melting-related phenomena represent fundamental material problems and are currently under intense experimental and theoretical study. They include surface premelting and melting below the thermodynamic melting temperature θe, caused by reduction in surface energy and leading to appearance of a molten, nanometer-thick layer1,2; reduction in melting temperature θm with reduction of the particle radius R down to nanoscale3,4; melting of particles with radii comparable to and smaller than the equilibrium solid–liquid interface width δe, which is a few nm3,5; and overheating above θe during very fast heating6,7. All of these phenomena allow one to determine the properties of solid and liquid deeply in the region of their metastability and even complete instability (that is, above the solid instability temperature θi or below the melt instability temperature θc, see Supplementary Fig. S1), and to study intermediate states, various scale effects and non-equilibrium thermodynamic and kinetic properties. These studies also have important applied aspects, for example, for combustion of Al nanoparticles8, which are the most known representatives of nanoenergetic materials. However, a consistent theoretical framework for the description of the above phenomena is lacking. The sharp-interface approach9 (SIA) is not justified for the above problems. Although there are important molecular dynamics (MD) studies5,6,10, we focus on the continuum phase-field approach (PFA), which allows consideration of larger spatial and time scales and operates explicitly with thermodynamic and kinetic parameters determined at the macroscale (see Supplementary Discussion). When mechanics is taken into account, a basic problem of the description of finite-width, solid–liquid interface appears. Traditionally, solids and liquids are described in completely different continuum mechanical frameworks (for example, solids are described in undeformed states, whereas liquids are described in a deformed state), which sophisticates the description of intermediate state. Some works consider solid as a very viscous liquid13, that is, neglect elastic shear modulus μ. Such a liquid–liquid interface is incoherent and does not generate internal elastic stresses, similar to sharp interface (Fig. 1). Alternatively14, solid–melt interface is considered as a coherent interface (Fig. 1), in which shear modulus varies from that for solid to zero, and this results in generation of internal elastic stresses at the interface. When particle size is comparable to or smaller than the interface width, a coherent interface is the only reasonable choice. Although this model is supposed to be more precise, the surface tension in it is not consistent with sharp-interface limit, even if μ=0. Also, even for liquid–liquid interface, expression for surface tension in PFA differs by a hydrostatic pressure from that in SIA11,12,13. This is a fundamental thermodynamic inconsistency, which is especially important for nanoscale interface radii.

Figure 1: Different types of interfaces between solid and molten phases.
figure 1

(a) Traditional sharp incoherent solid–melt interface, which does not generate internal elastic stresses. (b) Incoherent, finite-width, solid–melt interface with zero shear modulus μ=0 that does not generate internal elastic stresses. (c) Coherent finite-width interface between two solid phases. Continuity of crystal lattice across the interface along with a change in the size of one of the lattices during transformation (due to transformation strain tensor ɛt) generates internal elastic stresses. (d) Coherent, finite-width, solid–melt interface with non-zero shear modulus μ≠0 that generates internal elastic stresses.

Full size image

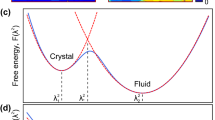
Surface premelting and melting were studied using PFA15,16,17 without involving mechanics. However, the employed equation for surface energy, γ(η)=a+bη2, did not allow a homogeneous solution for solid (η=1) (Fig. 2), exhibiting a surface disordered structure even below melt instability temperature θc, when the energy minimum corresponding to melt does not exist. Such an inconsistency also exhibits itself in unphysical regions in the phase diagram15.

Figure 2: Stationary solutions for Ginzburg–Landau equation with different models for surface energy.
figure 2

Previous models15,16,17 (blue line) did not allow a homogeneous solution for the solid (η=1), exhibiting a surface disordered structure at any temperature. Our model equation (8) (red line) is developed using the condition that it allows a homogeneous solution for the solid. The green line represents melt (η=0).

Full size image

The goal of this paper is to develop a unified PFA coupled to mechanics and reveal the non-trivial features of the above melt-related phenomena. Thus, a model with coherent solid–melt interface is developed (see Fig. 1), in which shear modulus μ varies from that for solid to zero, and this results in generation of internal elastic stresses at the interface. Thermodynamic potential in this model results in surface-tension stresses consistent with the SIA, in contrast to known models with incoherent interface (for which μ=0)11,12,13 and coherent interface14. Also, the necessity of introducing a non-spherical transformation strain, which, in addition to volumetric expansion during melting, describes change in shape, is demonstrated. Our model resolves fundamental thermodynamic inconsistency and includes more advanced mechanics, which is especially important for nanoparticles. Also, a model for surface energy that varies during melting is developed, which resolves the aforementioned non-physical effects in existing models15,16,17 and adds mechanics to them. It is demonstrated that our model describes well experimental data on the width of the molten layer versus temperature for the Al plane surface, and then it is applied to surface-induced premelting and barrierless melt nucleation for nanoparticles. It also describes well experimental data on θm versus R, even better than MD simulations5. Then, non-equilibrium and small-scale regimes were treated, that is, interface profile, width, energy and velocity have been determined and analysed versus R, interface position ri, and large overheating and heating rates ħ. Thus, the derived analytical expression for interface velocity v describes well simulation results well outside an expected range, namely, even for θ>θi, ħ up to 1013 K s−1, and ri≥2 δe. It also describes well the effect of large compressive and tensile pressure. Homogeneous melt nucleation competes for ħ=1013 K s−1 with interface propagation. For R=1 and 3 nm, premelting occurs in the entire particle rather than at the surface only. Allowing for mechanics increases the melting temperature by 70 K for R=1 nm particle due to pressure induced by surface tension. For R≤1.5 nm, θm<θc, that is, the particle melts more than 200 K below θe, while there is no local energy minimum corresponding to melt. While for a liquid–liquid interface our calculations reproduce the Laplace relationship for jump in radial stresses Δσr, for coherent solid–melt interface, Δσr does not follow the Laplace relationship and even may possess the opposite sign, causing tension in the solid core instead of compression. Interface energy varies in a non-trivial way for ri≤4δe≃12 nm with decreasing ri, increasing for θ>θe and decreasing for θ<θe; this is opposite to the behaviour for ri>12 nm.

Results

Theory

We designate contractions of tensors A={Aij} and B={Bji} over one and two indices as A·B={Aij Bjk} and A:B=Aij Bji, respectively. The subscript * means symmetrization; the subscripts or superscripts e, θ and t are for elastic, thermal and transformational contributions to strain and energy; I is the unit tensor; ΔA=As−Am for any property A, with subscripts s and m denoting solid and melt, respectively; and are the gradient operators in the undeformed and deformed states; and ⊗ designates a dyadic product.

To develop a unified approach to solid and liquid, we will consider liquid as the limit case of isotropic viscoelastic solid with μ=0. For simplicity, viscosity is neglected, isothermal processes are considered and shear strain is small. However, even if volumetric strain ɛ0 is small, in order to reproduce surface tension one has to use fully large-strain formulation (see below). We will modify our recently developed theory of martensitic transformations in solids18,19 to describe melting. The Helmholtz free energy per unit undeformed volume of solid ψ=ψ(ɛ, η, η, θ), in which ɛ is the strain tensor and η is the order parameter that varies from 1 in solid to 0 in melt. Using an irreversible thermodynamic procedure based on the application of the first and second laws of thermodynamics to the system with energy depending on the gradient of the order parameter (see ref. 12 and references in it) and assuming linear relation between thermodynamic force and flux, one obtains expression for the stress tensor σ and the Ginzburg–Landau (GL) equation

in which ρ0 and ρ are the mass densities in the non-deformed and deformed states, χ is the kinetic coefficient, and ɛ=const while evaluating ∂ψ/∂η. The kinematics relationship between displacement u and strain ɛ=1/3ɛ0I+e, decomposition of ɛ and the equilibrium equation are given by

in which e is the deviatoric strain. Energies and strains are defined as follows:

Here K is the bulk modulus, β and α are the gradient energy and linear thermal expansion coefficients, H is the heat of fusion, is the double-well energy, and is the transformation strain that transforms the elemental volume of solid to melt under σ=0. While for martensitic phase transformations is a tensor connecting two crystal lattices, for melting it is always pure volumetric strain, 9,11,12,13,14. We will show that the usual assumption causes very high internal stresses and elastic energy within the interface, which suppresses melt nucleation and contradicts with the experiment. Development of a complete theory for is not a goal of this paper, but we consider an alternative expression for uniaxial , in which is the unit normal to the interface. In this case, the component of transformation strain along the interface is absent, which minimizes internal stresses and their energy. Then equation (1) looks like

in which σe and σst are the elastic stress and surface tension, σe=pe for volumetric transformation strain and σe=k·σe·k for uniaxial transformation strain. For a phase-equilibrium condition in the stress-free case, (ref. 20), and we have σst=β|η|2(I−k⊗k), that is, it represents two equal normal stresses along the interface. Thus, σst is consistent with the SIA, unlike previous approaches11,12,13,14, which resolves a long-standing problem in PFA for melting.

In contrast to previous works on melting and other transformations in solids14,18, the gradient operator with respect to the deformed state was used, and the finite-strain factor J was included in the proper places. Although use of is natural for liquids11,12,13, this is not the case for solids. One of the unexpected points is that even for small strains, one cannot assume that J≃1 and , because this leads to zero surface tension. The same thermodynamic procedure19 that led to equation (1) also results in the boundary conditions

in which n is the unit normal to the boundary, σn is the normal to interface stress, 1/R is the mean curvature and is the external pressure. Equation (8) represents a generalization for the 3-D case and coupling with mechanics of known condition15,16. We require the following properties of the surface energy: γ(0)=γl; γ(1)=γs; . The last equation guarantees that homogeneous melt (η=0) and solid (η=1) satisfy equation (8) and removes contradiction in the known papers15,16 (see Fig. 2). These properties are met for polynomial γ(η)=γl+Δγ(aη2+(4−2a)η3+(a−3)η4) of the lowest degree with a parameter a. One can demonstrate that a criterion of barrierless surface-induced melt nucleation is consistent with a sharp-interface condition, Δγ>γs−l, when a=3. Then γ(η)=γl+Δγφ(η). If surface energy does not change during melting, then γ=const and equation (8) reduces to traditional boundary condition η·n=0.

We focus on Al nanoparticles; material parameters are given in Supplementary Discussion. In particular, θe=933.67 K, θc=0.8θe=746.9 K and θi=1.2θe=1120.4 K, δe=2.97 nm. Note that all material parameters have been obtained for a macroscopic sample with no fitting parameters left. None of our developments (coherent interface with uniaxial transformation strain, expressions for free energy that result in correct expression for surface tension, and expression for surface energy) requires additional material parameters. First, homogeneous heating of particles of radius R was considered and stationary solutions were found for each temperature. The thickness h of pre-molten and completely molten surface layer (determined by an interphase radius ri, that is, by point with η=0.5) have been plotted versus θe−θ (Fig. 3). At melting temperature, θm, the stationary, two-phase solution ceases to exist and interface propagates to the centre.

Figure 3: Thickness of molten surface layer versus temperature for different particle radii.
figure 3

Each colour represents a particle radius shown in nm near the curves. Solid lines are results of the GL model without mechanics. Dotted and dashed lines are obtained for coupled GL and mechanics model with volumetric and uniaxial transformation strains, respectively. Black dots are experimental data1 obtained using medium-energy ion scattering. Experimental points for a plane surface are close to the calculations for infinite radius for GL and coupled models with uniaxial transformation strain. All curves, excluding those interrupted at 0.1 K, are ended at the melting temperature.

Full size image

Size dependence of melting temperature

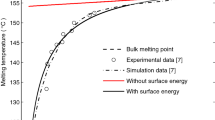
In Figure 4, the lowest curve is for GL equation only, that is, for neglected mechanics. Below radius R*=6.12 nm, results for volumetric ɛt give slightly lower θm and are closer to the experimental points, whereas for R>R* results for uniaxial ɛt are much lower. For R>21.2 nm and volumetric ɛt, θm>θe. This is in contrast to the experiments for flat interface, for which θm=θe. That is why uniaxial transformation strain was used, in contrast to known models11,12,13. For neglected mechanics and for uniaxial ɛt, melting temperature tends to θe for infinite radius. Experimental points are between curves with neglected mechanics and for uniaxial ɛt for R>R* and for volumetric ɛt for R<R*. Coupling with mechanics for 2–3 nm particles increases the melting temperature by 30–40 K (see also Fig. 5) and makes it closer to the experiments. Surprisingly, our results are in better correspondence with experiments than known MD approaches (Fig. 4b). Thus, we can conclude that the model of coherent solid–melt interface has good potential for the description of experiments; traditional volumetric ɛt is not adequate for large particles, that is, there is interface restructuring, driven by the internal stress relaxation, and a thermodynamic and kinetic theory for et should be developed.

Figure 4: Melting temperature of Al versus particle radius.
figure 4

(a) Curves are calculated using three models: GL equations only (GL, green line), GL equation coupled to mechanics with volumetric (ɛt0) (red line) and uniaxial (ɛtr) (black dotted line) transformation strain. Dots are experimental data from Lai et al.3 obtained using thin-film differential scanning calorimetry. The horizontal line is the equilibrium temperature (the same curve designations are used in b). (b) Molecular dynamics results are added for particles with radii in the 1–6 nm range. Gray and blue lines are MD results5 using glue and embedded atom potentials, respectively.

Full size image
Figure 5: Stationary interface profiles φ(η) for Al particles for different temperatures.
figure 5

(a) R=1 nm; (b) R=3 nm. Solid lines are the results obtained with the GL model. Dotted and dashed lines are obtained using coupled GL and mechanics models with volumetric and uniaxial transformation strains, respectively. Different temperatures are considered for each model, which are designated on the graphs. The lowest curve for each model corresponds to the melting temperature.

Full size image

Surface premelting and melting

As shown in Figure 3, for a plane interface (R→∞), plots for thickness of the molten layer versus θ for GL and uniaxial ɛt almost coincide and are very close to experimental points, which justifies the validity of our model for surface energy. Results for volumetric ɛt are inconsistent with experiments. For nanoparticles, h(θ) plots consist of two parts: an almost straight line with small slope at high temperature with transition to an almost vertical line for temperatures close to θm. The maximum thickness of the molten layer is very close for the GL model and the model with uniaxial ɛt. Although curves for these models look also close, for some temperatures the difference in thickness is a factor of 2 or larger. For R≤5 nm, curves for volumetric and uniaxial ɛt are very close.

Stationary distributions of interface profiles φ(η) (note that φ(η) rather than η describes the variation of all properties, see equation (1)) in particles of R=1 and 3 nm are presented in Figure 5. For all cases, the complete liquid phase (η=0) is not reached. For 1 and 3 nm, stationary premelting (that is, φ(η)<1) occurs in the entire particle rather than at the surface only. Allowing for mechanics increases the melting temperature by 70 K for the R=1 nm particle, mostly due to pressure induced by surface tension. Note that for R<1.5 nm, one has θm<θc, that is, the particle melts even when bulk melt is unstable.

Surface tension

Distributions of radial stresses along r are shown in Figure 6. When internal elastic stresses can be neglected (for equal thermoelastic properties of phases and μ=0, that is, for liquid–liquid transformation, or for ɛt=0), our calculations at θe reproduce the Laplace relationship for jump in radial stresses Δσr=−2γs−l/ri within an error of 0.14% for ri>11 nm and 1.03% at ri=5 nm. For actual solid-melt properties and volumetric ɛt, Δσr does not follow the Laplace relationship and even possesses the opposite sign, causing tension in the solid core (Fig. 6). For uniaxial ɛt, Δσr=−k2γs−l/ri with k>1.

Figure 6: Distribution of radial stresses for three interface positions.
figure 6

The blue line corresponds to the interface radius at 30 nm, the red at 20 nm, and the green at 10 nm. Distributions are calculated at θe using models with volumetric (ɛt0) (dotted line) and uniaxial (ɛtr) (dashed line) transformation strains, as well as with equal thermoelastic properties of solid and melt (solid line), that is, for liquid–liquid transformation. Dots designate pressures in melt ps+2γs−l/ri based on the Laplace equation that coincides with results of calculations for equal thermoelastic properties of the solid and melt.

Full size image

Interface profile and energy

For plane interface, θ=θe, and neglected mechanics, the GL equation allows analytical solution for an equilibrium interface:

where the interface width is δ=|rl−rs| and rl and rs are determined from the conditions φ(η)=0.01 and 0.99, respectively. Surface energy in non-equilibrium state is defined as an excess energy with respect to solid (where 0.5<η≤1) and liquid (where 0≤η≤0.5)

With neglected mechanics, interface width is described by equation (9) within 2.5% error for ri≥2δe and θ≤1.25θe, that is, even above θi. For ri=2 nm, δ=3.99 nm=1.34δe. Mechanics slightly (<1%) increases the width for θ=θe, but this difference grows with increasing temperature; for example, δ=3.03 and 3.06 nm for ri=30 nm, θ=1.2θe and 1.25θe, respectively. Still, the interface profile differs from equation (9) within Δφ=0.03 error for ri≥δe/2 and θ≤θi. Interface energy versus interface radius for different temperatures is shown in Figure 7. For equilibrium temperature, interface energy starts growing for ri<10 nm and maximum deviation from γs−l=0.1 J m−2 is 11.2% for the smallest ri=2.41 nm, for which full interface exists. For ri>20 nm expected decrease in with growing temperature is observed. For ri<20 nm, unexpectedly the opposite relation is found, which means change in sign of the interface entropy. Note that for ri>4δe≃12 nm, deviation of from γs−l does not exceed 3% in the entire temperature range θc<θ<θi, which is well below the inaccuracy of experimental data for interface energy.

Figure 7: Non-equilibrium interface energy versus interface radius for different temperatures.
figure 7

Results are obtained for both volumetric and uniaxial transformation strains and practically coincide. At the position of ri=10 nm, curves from top to bottom correspond to temperatures of 1.2θe, 1.1θe, θe, 0.9θe and 0.8θe. A crossover in temperature dependence of interface energy for radii below 20 nm is evident.

Full size image

Interface velocity

When internal stresses inside an interface are neglected, the following linear relationship is obtained for ri≫δe between interface velocity v0 and the thermodynamic force for interface propagation per unit deformed volume of solid X:

It can be seen from Figure 8 that equation (11) describes well (error ≤3%) results of our simulations even for ri>2δe for neglected internal stresses and for heating rates as high as 1013 K s−1. Owing to small particle size, homogeneous temperature is assumed; see the analytical justification in ref. 8. The temperature at some points in Figure 8 significantly exceeds the instability temperature θi and reaches 1344 K for 1013 K s−1; that is why interface does not reach the centre of the particle, because homogeneous reduction of η in the central part completes melting faster. Even for high compressive and tensile pressures, equation (11) works well when internal stresses are negligible: for external pressure p=4 GPa and θ=1225 K deviations from simulations for ri=30 and 20 nm are within 2.14%, and for p=−4 GPa and θ=750 K it is within 1.05%. Velocities for volumetric ɛt are higher, and for uniaxial ɛt they are lower than for the case with μ=0.

Figure 8: Interface velocity versus position for three heating rates.
figure 8

The heating rate is 109 K s−1 at the bottom, 1012 K s−1 in the middle, and 1013 K s−1 at the top. Curves correspond to PFA with different models (red line for GL model, green and black lines for models with volumetric and uniaxial transformation strains, respectively, and blue line for volumetric transformation strain with equal solid and melt properties). Points correspond to SIA, namely, to equation (11).

Full size image

Discussion

Note that the SIA21 to melting/solidification at the nanoscale, which includes surface-induced melting and coupled to mechanics, can be applied to our problems down to some radius, which is to be determined by comparison with PFA. However, when the interface region is a significant part of the particle, PFA is more precise and does not require any adjustments. In contrast, SIA should incorporate the size dependence of surface melting (Fig. 3), size and temperature dependence of surface energy (Fig. 7), and surface stresses not equal to surface tension (Fig. 6). To summarize, an advanced phase-field approach to premelting and melting coupled to mechanics is developed. It is applied to study melting deeply in the region of metastability and complete instability of solid and melt, intermediate states at the surface and in few nm-size particles, scale effect, and non-equilibrium thermodynamic and kinetic properties. The importance of mechanics effects (even without external pressure) is elucidated. Crossover in temperature dependence of the interface energy for radii below 20 nm and violation of the Laplace relationship for the jump in pressure is obtained. Conceptual validity of the coherent solid melt is proven and necessity for its further development, namely, formulation of the evolution equation for the deviatoric part of ɛt, is demonstrated.

Methods

The finite element method code COMSOL Multiphysics was utilized to solve coupled equations (2), (3), (4), (5), (6), (7), (8).

Quadratic Lagrangian elements are used for both the mechanical and GL differential equations. In all, 15–30 elements per interface width and an adaptive time step with a minimum of 1,000 time steps for a typical non-stationary problem are used. To check the model, interface profiles are compared with analytical results for plane interface at equilibrium temperature22. Even with an interface radius of 30 nm, difference between planar analytical solution and COMSOL GL result is less than 0.1%. Also, the solid–liquid interface energy in Al practically coincides with its analytical value of 0.1 J m−2, see Figure 7.

Additional information

How to cite this article: Levitas, V.I. & Samani. K. Size and mechanics effects in surface-induced melting of nanoparticles. Nat. Commun. 2:284 doi: 10.1038/ncomms1275 (2011).