Main

Pioneering technological developments have enabled the trapping, accumulation and delivery8,9,10 of positrons for study of their fundamental interactions with atoms and molecules1,12, and the formation, exploitation and interrogation of positronium (Ps)13,14 and antihydrogen15,16. The ability of positrons to annihilate with atomic electrons forming characteristic γ-rays makes them a unique probe over vast length scales, giving them important use in, for example, materials science for ultrasensitive diagnostics of industrially important materials7,8, medical imaging (positron emission tomography)17 and astrophysics11.

Proper interpretation of the materials science techniques and the development of next-generation antimatter-based technologies rely on an accurate understanding of the fundamental interactions of positrons with atoms and molecules. Substantial progress has been made developing ab initio theoretical understanding of positron–atom interactions1,12,18,19,20,21. Yet, for molecules, clusters and condensed matter, many basic aspects of positron–matter interactions remain poorly understood, and predictive capability is lacking. A notable example is the open fundamental problem of positron binding to molecules. Observation of energy-resolved annihilation spectra have enabled measurement of positron binding energies (ranging from a few to a few hundred meV) for more than 90 molecules2,3,4,5,6. The majority of these (approximately 60) are nonpolar or weakly polar species, such as alkanes, aromatics, partially halogenated hydrocarbons, alcohols, formates and acetates. By contrast, ab initio calculations have been performed predominantly for strongly polar molecules1 (though we note recent model calculations for polar and nonpolar molecules)22,23. Only six species have been studied both experimentally and with ab initio theory, via configuration interaction (CI)24,25,26,27,28 and ‘any particle molecular orbital’ (APMO)29 approaches: carbon disulfide CS2, acetaldehyde C2H4O, propanal C2H5CHO, acetone (CH3)2CO, acetonitrile CH3CN, and propionitrile C2H5CN1. For these, the sophisticated CI and APMO approaches proved deficient, greatly underestimating the experimental binding energies, agreeing to at best greater than approximately 25% (for acetonitrile, theory28: εb = 136 meV, versus experiment5: εb = 180 meV), and failing to predict binding in nonpolar CS2 (versus experiment: εb = 75 meV)4 (see below). Also, the considerably larger positron–molecule binding energies compared to electron–molecule ones (that is, negative ion states)4,6 are not quantitatively understood.

Table 1 Calculated positron–molecule binding energies
Full size table

For these molecules, vibrational and geometry relaxation effects are known to provide only a few per cent correction to fixed-nuclei calculations of binding energies and wavefunction densities1,28,29,30,31,32: for example, for acetaldehyde, acetone and acetonitrile (all considered in this work) the vibrational averaging correction was approximately 1–5%28. The theoretical difficulty lies in the need to identify and accurately describe strong many-body correlations that dominate the positron–molecule system. A powerful method that can fully account for the important correlations in a natural, intuitive and systematically improvable way is many-body theory19,33,34,35,36,37,38,39.

Here we develop the many-body theory of positron interactions with polyatomic molecules. We quantify and delineate the role of the correlations including polarization of the molecular electron cloud, screening of the positron–electron Coulomb interaction, and the unique process of virtual-Ps formation. We use the fixed-nuclei approximation and restrict to molecules with ionization energies larger than the Ps ground-state energy: for these, the Ps-formation channel is closed and the process is virtual, yet we will see that it has an important effect. After benchmarking its state-of-the-art computational implementation against explicitly correlated Gaussian (ECG) and quantum Monte Carlo (QMC) results for LiH and formaldehyde, we calculate binding energies and annihilation lifetimes for the six molecules for which both previous theory and measurements exist, finding excellent overall agreement. We additionally predict binding in formamide, CSe2, benzene and the primary nucleobases.

The positron binding energy ε and bound-state wavefunction ψε is found by solving the Dyson equation33 (H(0) + Σε)ψε(r) = εψε(r), where H(0) is the Hamiltonian of the positron in the Hartree–Fock field of the ground-state molecule, ΣE is a nonlocal, energy-dependent correlation potential (irreducible self energy of the positron), and r is positron coordinate. It acts as an integral operator ΣEψ(r) ≡ ∫(ΣE(r, r′))ψ(r′)dr′ and encapsulates the full complexity of the many-body problem. We calculate Σ via its expansion in residual electron–electron and electron–positron interactions, see Fig. 1. In Fig. 1a, the ‘GW’ self energy, ΣGW, describes the positron-induced polarization of the molecular electron cloud, and corrections to it owing to screening of the electron–positron Coulomb interaction by the molecular electrons, and electron–hole attractions (the Bethe–Salpeter equation approximation, GW@BSE). Figure 1b represents virtual-Ps formation19,39: it is denoted by ΣΓ and involves the summed infinite ladder series of (screened) electron–positron interactions (the ‘Γ block’; see Extended Data Fig. 1). The infinite ladder series is important to the positron problem because successive diagrams in this series contribute to the positron–molecule self energy with the same sign, whereas for all-electron systems the series is sign alternating and gives a small overall contribution. We also consider the smaller positron–hole ladder series contribution, ΣΛ, shown in Fig. 1c. The construction of Σ and solution of the Dyson equation are detailed in Methods.

Fig. 1: Main contributions to the positron–molecule self energy.
figure 1

a, The ‘GW’ contribution, which involves the positron Green’s function Gν and the (dynamic part of the) screened Coulomb interaction W. It describes the positron-induced polarization of the molecular electron cloud and corrections to it due to screening of the electron–positron Coulomb interaction by molecular electrons, and electron–hole attractions. b, The virtual-Ps contribution ΣΓ, which includes the summed infinite ladder series (‘Γ block’) of screened electron–positron interactions. c, The positron–hole ladder series (the ‘Λ block’) contribution ΣΛ. Lines directed to the right (left) represent particles (holes) propagating on the N-electron ground-state molecule: red lines labelled ε represent the external positron state; other red (blue) lines represent positron (excited electron or hole) intermediate states that are summed over; single (double) wavy lines represent bare (screened) Coulomb interactions. See Methods and Extended Data Fig. 1 for details of their calculation via the BSE.

Full size image

Positron binding energies and lifetimes

Table 1 shows our calculated binding energies at successively more sophisticated approximations to the correlation potential: Hartree–Fock, Σ(2) (bare polarization), ΣGW (polarization including electron screening and screened electron–hole interactions; Fig. 1a), ΣGW+Γ (Fig. 1a, b), and ΣGW+Γ+Λ (Fig. 1a–c). In the table, the first (second) number is the result using bare (dressed) Coulomb interactions in the ladders, and the third (our most sophisticated, in bold) is that using dressed interactions and energies. See also Fig. 2 for a graphical comparison of theory and experiment, and Extended Data Table 2 for more details.

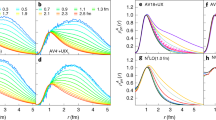
Fig. 2: Positron–molecule binding energies and bound-state Dyson wavefunction densities.
figure 2

a, The comparison of the present many-body calculations (red circles) with experiment (error bars for the calculations show the largest difference between the three ΣGW+Γ+Λ calculations in Table 1). Also shown are the CI and APMO calculations (blue squares and green crosses, respectively). MBT, many-body theory. b–l, Positron wavefunction densities. b, LiH, with Li atom at origin and H at approximately 3 a.u. along the molecular axis, showing the positron wavefunction density isosurface at 70% of the maximum (red lobe), the electron HOMO wavefunction density isosurface (blue lobe is the negative region at 40% of maximum, and brown is the positive region at 10% of the maximum). Also shown is the positron wavefunction calculated along the molecular axis in the Hartree–Fock approximation (black curve) and at the ΣGW+Γ+Λ level of many-body theory (red curve). c–i, The positron wavefunction density isosurfaces at 80% of maximum for formaldehyde (c), acetonitrile (d), propionitrile (e), acetone (f), propanal (g), acetaldehyde (h), and formamide (i). j–l, Nonpolar molecules with isosurfaces at 90% of maximum CS2 (j), CSe2 (k), and benzene (l). a.u., atomic units.

Source data

Full size image

Benchmarking and general trends

We benchmark our approach against ECG (εb = 1,043 meV)40 and QMC (εb = 1,015 meV)41 calculations for LiH, and against QMC for formaldehyde (εb = 25 ± 3 meV)42. The LiH results demonstrate the general trends seen in all the molecules considered. The Hartree–Fock binding energy (εb = 130 meV) is severely deficient. Including the bare polarization attraction Σ(2) considerably increases the binding energy (to εb = 434 meV). The addition of short-range screening corrections reduces the polarizability and binding energy (to εb = 336 meV, see Extended Data Table 2), but this is compensated by the inclusion of the electron–hole attractions (ΣGW: εb = 518 meV). This is still, however, less than half of the ECG result. The previous CI calculation24 is similarly deficient. Notably, however, including the virtual-Ps formation correlation potential (ΣGW+Γ) strongly enhances the binding, more than doubling it (to εb = 1,291 meV). Including the positron–hole ladder (ΣGW+Γ+Λ) slightly reduces binding (to εb = 1,106 meV); using screened interactions in the ladders reduces it slightly further (εb = 1,038 meV); additionally using the dressed energies in the diagram construction gives εb = 1,060 meV, agreeing with the ECG (QMC) result to within approximately 1% (approximately 4%). For formaldehyde, the addition of virtual-Ps again drastically enhances binding (by a factor of approximately 5 over the GW result), and including the positron–hole interaction results in a binding energy εb = 28 meV, within the error of the QMC calculation. Comparing to our method, the ECG and QMC approaches evidently account for virtual-Ps formation to a similar accuracy, although these methods cannot be scaled to larger molecules40, and provide relatively limited insight (see below). Additionally, the correlations effect a strong localization of the positron wavefunction density at the negatively charged end of the molecule (see Fig. 2), although overall, the wavefunction is quite diffuse, asymptotically taking the form ψ ∝ e−κr where \(\kappa =\sqrt{2{\varepsilon }_{{\rm{b}}}}\). We also calculate the positron Dyson wavefunction renormalization constants a (see equation (7) in Methods and Extended Data Table 2). These represent the contribution of the positron plus molecule in the ground-state component to the bound state. Their closeness to unity suggests the picture of a positron bound to the neutral molecule (instead of a Ps atom orbiting a molecular cation)43.

Comparison with experiment and previous theory

The best prior agreement between theory and experiment for any molecule was for acetonitrile (greater than approximately 25%). Considering the polar molecules first (Table 1 and Fig. 2), we immediately see that our full many-body theory (ΣGW+Γ+Λ) is superior, giving near-exact agreement (less than about 1% level) with experiment for propionitrile, propanal, acetaldehyde and formamide, and within 10% for acetonitrile and acetone (including the experimental error). (Overall we find excellent convergence in our calculation: see Methods and Extended Data Fig. 2). For all the polar molecules, the Hartree–Fock and bare (Σ(2)) and dressed (GW) polarization potentials substantially underestimate binding. The effect of virtual Ps is crucial: it enhances the binding energy by a factor of approximately 2 and is essential to bring theory into agreement with experiment. We note that the previous CI and APMO (‘REN-PP3’, which uses a diagonal approximation and does not explicitly account for virtual-Ps formation) calculations are severely deficient.

For the nonpolar molecules, we find that binding is exclusively enabled by correlations. For CS2 a considerable binding energy of 75 meV was measured, whereas the CI calculation failed to predict binding27. We see that polarization (GW) alone is insufficient to support binding. Notably, however, including the virtual-Ps contribution results in a prediction of large binding: our ΣGW+Γ+Λ result of εb = 63 meV is close to experiment. For the nonpolar molecules the positron wavefunction is delocalized around the molecule (Fig. 2j–l), making the accurate description of virtual-Ps more computationally demanding. For CSe2 and benzene, in contrast to the molecules already considered, we have not optimized the bases (accurate calculation for these molecules require computational resources currently beyond our disposal) and our values for εb should be considered as lower bounds. Nevertheless, the results further elucidate the essential role of virtual-Ps formation in enabling (large) binding, and the positron wavefunctions provide fundamental insight that may prove instructive to refine ab initio and model calculations (see "Predicting binding in larger molecules: nucleobases").

Prediction for formamide

For formamide, the archetypal molecule for the investigation of protein and peptide chemistry, we are unaware of any prior calculation. We predict binding (εb ≈ 189 meV). Preliminary experiments see evidence of εb ≈ 200 meV, although a final value has yet to be determined (J. R. Danielson, S. Ghosh & C. M. Surko, unpublished material).

Molecular orbital contributions to binding

At the static Hartree–Fock level, we find εb to be (monotonically and nonlinearly) related to the permanent dipole moment (expected from the dipole-potential model)44. Ultimately the correlation potential is anisotropic (see Extended Data Table 1 for calculated anisotropic polarizabilities), and depends nonlinearly on the polarizabilities and ionization energies of the individual molecular orbitals. Moreover, the binding energy depends nonlinearly on the correlation potential (for example, see Extended Data Fig. 3). The ordering of εb with respect to dipole moment persists to the Σ(2+Γ+Λ) calculation, with the exception of acetaldehyde and propanal, and we note that for acetone, correlations considerably enhance εb. It is instructive to consider the dimensionless quantity45 \({\mathscr{S}}=-{\sum }_{\nu > 0}{\varepsilon }_{\nu }^{-1}\langle \nu |{\Sigma }|\nu \rangle \) (where the sum is over excited Hartree–Fock positron basis states of energy εν, see Methods), which gives an effective measure of the strength of the correlation potential Σ. The magnitudes of the strength of Σ(2), \({{\mathscr{S}}}^{(2)}\) ranges from 4–15 (see Extended Data Table 2), and follows the ordering of the isotropic polarizability, with the exception of acetone and propanal (acetone has a larger polarizability and smaller ionization energy than propanal), and benzene and CSe2 (owing to benzene’s π bonds; see below). This suggests that (the short-range contributions to) Σ(2) cannot be parametrized solely by the polarizability. Similarly, the magnitudes of \({{\mathscr{S}}}^{(\Gamma )}\) (ranging from 2–5) do not strictly follow the ordering of the ionization energies. To illuminate this, note that at the bare-polarization approximation, Σ(2), and polarization plus virtual-Ps formation approximation, Σ(2+Γ) = Σ(2) + Σ(Γ), we can delineate the contribution of individual molecular orbitals to positron binding. Figure 3a shows the partial \({{\mathscr{S}}}^{({\Gamma })}\) and \({{\mathscr{S}}}^{(2+{\Gamma })}\) for individual occupied molecular orbitals against their respective ionization energies, and the ratio \(g\equiv {{\mathscr{S}}}^{(2+{\Gamma })}/{{\mathscr{S}}}^{(2)}\), where \({{\mathscr{S}}}^{(2)}={{\mathscr{S}}}^{(2+{\Gamma })}-{{\mathscr{S}}}^{({\Gamma })}\). Both \({{\mathscr{S}}}^{({\Gamma })}\) and \({{\mathscr{S}}}^{(2+{\Gamma })}\) decrease from the Ps-formation threshold to higher ionization energies: it is more difficult to perturb more tightly bound electrons. However, the decrease is not monotonic: we see that despite having larger ionization energies, π-type electronic molecular orbitals below the highest occupied molecular orbital (HOMO) can contribute considerably more than a σ-type HOMO to \({{\mathscr{S}}}^{({\Gamma })}\) and \({{\mathscr{S}}}^{(2+{\Gamma })}\)—for example, in acetone, propanal and acetaldehyde, the strength of the π-type (H−1)OMO is larger than the σ-type HOMO, and in propanal, the (H−3)OMO of π type contributes more strongly than the (H−2)OMO, and so on. It was previously speculated3 that π bonds were important due to the ability of the positron to more easily access electron density that is delocalized from (repulsive) nuclei. This is borne out by our calculations, and we see in Fig. 3b that considerable positron density protrudes into the region of the π bond. Acetonitrile and propionitrile have a doubly degenerate π HOMO of large strength. For acetonitrile this results in a larger strength parameter than formamide.

Fig. 3: Molecular orbital contributions to binding, and scaling formula for large molecules.
figure 3

a, Molecular orbital contribution to the dimensionless strength of the virtual-Ps formation correlation potential \({{\mathscr{S}}}^{({\Gamma })}\) (circles) and including bare polarization \({{\mathscr{S}}}^{(2+{\Gamma })}\) (squares) and the ratio \(g\equiv {{\mathscr{S}}}^{(2+{\Gamma })}/{{\mathscr{S}}}^{(2)}\) (crosses, where \({{\mathscr{S}}}^{(2)}={{\mathscr{S}}}^{(2+{\Gamma })}-{{\mathscr{S}}}^{({\Gamma })}\)) against \( {\mathcal I} \,=\,I\,-\,|{E}_{{\rm{Ps}}}|\), where I is the molecular orbital ionization energy and EPs = −6.8 eV is the ground-state energy of Ps. Arrows on \({{\mathscr{S}}}^{(2+{\Gamma })}\) mark π orbitals with I < 15 eV, and inset molecular orbital plots show HOMO (σ-type) and next HOMO (π-type) in acetaldehyde (solid red and blue: positive and negative regions of electronic molecular orbital; red wireframe: positron density at 85% of maximum). Dashed lines show the fits \({\mathscr{S}}\approx a{{\rm{e}}}^{-b {\mathcal I} }+c{ {\mathcal I} }^{-d}\) with a = 0.67 (2.57); b = 0.121 (0.092); c = 2.51 (6.64); d = 1.38 (1.37) for \({{\mathscr{S}}}^{(\Gamma )}\) (\({{\mathscr{S}}}^{(2+{\Gamma })}\)). b, The positron wavefunction density in acetaldehyde (in the plane containing the CO bond perpendicular to the CCO plane), which protrudes along the π bond. c, Comparison of binding energies for the molecules in a calculated using Σ = ΣGW+Γ+Λ and accounting for (the computationally demanding to calculate) ΣΓ via Σ = gΣ(2) + ΣΛ, for g = 1.4 (circles) and 1.5 (squares) (see text). d, εb in nucleobases, calculated with Σ ≈ gΣ(2) + ΣΛ for g = 1.4 and g = 1.5. HF, Hartree–Fock; MBT, many-body theory.

Source data

Full size image

Predicting binding in larger molecules: nucleobases

The ratio \(g\equiv {{\mathscr{S}}}^{(2+{\Gamma })}/{{\mathscr{S}}}^{(2)}\) depends weakly on the ionization energy, with a value of approximately 1.4–1.5 for the HOMOs (I ≈ 10 eV). We propose that binding energies of large molecules (for example, 15–100 atoms, for which a converged calculation of the virtual-Ps diagram (Fig. 1b) may be too computationally demanding) can be calculated by approximating Σ ≈ gΣ(2) + ΣΛ. As well as accounting for virtual-Ps formation, this model potential reflects the anisotropy of the true interactions. For the molecules considered in Table 1, this works well (see Fig. 3c and Extended Data Fig. 3). Using this approximation, we calculate the positron binding energy in the five primary nucleobases (Fig. 3d). Our results are larger than the previous APMO calculations, mirroring the results for the molecules in Table 1. Notably, we predict binding in adenine.

Positron lifetimes

We also calculate the annihilation lifetime of the bound positron (see Methods and Extended Data Figs. 4, 5), finding that the correlations reduce it by approximately 2–3 orders of magnitude to τ ≈ 1 ns. The partial annihilation rates on individual occupied electron orbitals are also calculated and are shown to depend strongly on the symmetry relative to that of the positron molecular orbital, with the HOMO not necessarily dominating, for example in acetonitrile and formamide. Such partial annihilation rates are required to properly interpret materials science experiments—for example, positron-annihilation-induced Auger electron spectroscopy7,8—and define the initial cationic wavepackets in positron-annihilation-induced charge migration46, relevant to, for example, base-selective oxidization of nucleobases47.

Future perspectives

Many-body theory has elucidated the long-standing correlation-dominated problem of positron binding to molecules. Benchmarking against ECG and QMC calculations for LiH and formaldehyde showed the many-body theory to be similarly accurate, but its power is that it can be extended to large molecules and provides additional fundamental insight. Importantly, the effects of correlations were quantified and delineated. In particular, the key role of virtual-Ps formation in greatly enhancing binding in polar molecules and exclusively enabling binding in nonpolar molecules, the near-cancellation of screening corrections to the bare polarization, and the non-negligible role of the positron–hole interaction were all identified. The contribution of individual molecular orbitals to the (anisotropic) correlation potential was quantified, and the importance of electronic π orbitals (previously speculated)3 was confirmed. For polar molecules the many-body theory gave binding energies in excellent (near exact, or within small error bars for most cases) agreement with the long-standing experiments. For nonpolar molecules, binding was predicted for CS2, CSe2 and benzene, with larger discrepancy (within less than approximately 20%) owing to slower convergence of the virtual-Ps contribution due to the delocalized positron wavefunction. We also predicted binding in formamide and the primary nucleobases. The excellent level of agreement with experiment reaffirms that for these molecules binding is dominated by correlations, and that vibrational effects are relatively small1,28,29,30,31,32. Complementary laser-assisted photorecombination experiments48 would provide direct comparison with our results, elucidating the problem in the absence of vibrations. Coupled-cluster34 and ADC36 calculations should also be possible and instructive.

The present calculations support resonant annihilation experiments and the related theory to which binding energies and annihilation lifetimes enter as parameters1. Beyond the fundamental insight immediately provided, the step-change in capability enables calculations of positron scattering and molecular-orbital-resolved, Doppler-broadened annihilation γ-ray spectra (underway), required to, for example, properly interpret positron-based ultrasensitive materials science techniques7,8, provide insight on molecular fragmentation10, and understand positron interactions in the Galaxy11 and living tissue (relevant to developing next-generation PET)49,50. It also provides a foundation for the implementation of inelastic38 (to include real Ps formation) and time-dependent51 molecular processes, to, for example, model positron-annihilation-induced Auger-electron spectroscopy8, interatomic Coulomb decay52, charge migration46 (including that relevant to medicine)47 and luminescence53, and for the study of vibrational effects via coupling of the nuclear and electronic degrees of freedom54. Finally, the difficulty of the positron–molecule problem presents a rich testbed for the development of other approaches to the many-body problem, for which our results can serve as benchmarks.

Methods

The Dyson equation in a Gaussian basis

We calculate the positron–molecule binding energy ε and quasiparticle wavefunction ψε by solving the Dyson equation. We take the zeroth-order Hamiltonian H(0) to be that of the positron in the Hartree–Fock field of the frozen-target N-electron ground-state molecule. The self-energy diagrams thus begin at second order in the Coulomb interaction. Instead of computing the self energy Σ(r,r′) in the coordinate basis, it is more convenient to work with its matrix elements in the Hartree–Fock basis. Specifically, we expand the electron (−) and positron (+) Hartree–Fock molecular orbitals \({\phi }_{a}^{\pm }({\bf{r}})\) in distinct Gaussian basis sets as \({\phi }_{a}^{\pm }({\bf{r}})={\sum }_{A}^{{N}_{c}^{\pm }}{\sum }_{k=1}^{{N}_{A}^{\pm }}{C}_{aAk}^{\pm }{\chi }_{{A}_{k}}^{\pm }({\bf{r}})\), where A labels the \({N}_{c}^{\pm }\) basis centres, k labels the \({N}_{A}^{\pm }\) different Gaussians on centre A, each taken to be of Cartesian type with angular momentum lx + ly + lz, and with \({\chi }_{{A}_{k}}({\bf{r}})={{\mathscr{N}}}_{{A}_{k}}{(x-{x}_{A})}^{{l}_{Ak}^{x}}{(y-{y}_{A})}^{{l}_{Ak}^{y}}{(z-{z}_{A})}^{{l}_{Ak}^{z}}\exp \{-{\zeta }_{Ak}|{\bf{r}}-{{\bf{r}}}_{A}{|}^{2}\}\), where \({{\mathscr{N}}}_{{A}_{k}}\) is a normalization constant, and C are the expansion coefficients to be determined (see later in this section). Molecular geometries are determined via minimization of the total electronic Hartree–Fock energy in the Molpro56,57 package, for the respective basis set (see next paragraph), ensuring an internally consistent ab initio calculation.

For both electrons and positrons, we use the diffuse-function-augmented correlation-consistent polarized aug-cc-pVXZ (X = T or Q) Dunning basis sets centred on all atomic nuclei of the molecule, which enables accurate determination of the electronic structure including cusps58 and expulsion of the positron density from the nuclei. To capture the long-range correlation effects, for the positron we also additionally include at least one large even-tempered set at the molecular centre or region of maximum positron density of the form Ns(N − 1)p(N − 2)d(N − 3)f(N − 4)g with N ≈ 10–15 (where it should be understood that the full degenerate set of nonzero angular momentum functions is used) and exponents \({\zeta }_{{A}_{k}}={\zeta }_{{A}_{1}}{\beta }^{k-1}\), k = 1, …, N, for each angular momentum type, where \({\zeta }_{{A}_{1}} > 0\) and β > 1 are parameters. The value of \({\zeta }_{{A}_{1}}\) is important because the bound positron wavefunction behaves asymptotically as ψ ∝ e−κr, where \(\kappa =\sqrt{2{\varepsilon }_{{\rm{b}}}}\). Thus, to ensure that the expansion describes the wavefunction well at r ≈ 1/κ—that is, that the broadest Gaussian covers the extent of the positron wavefunction—one must have \({\zeta }_{{A}_{1}}\lesssim {\kappa }^{2}=2{\varepsilon }_{{\rm{b}}}\). In practice we performed binding energy calculations for a range of \({\zeta }_{{A}_{1}}\) and β for each molecule, finding that there are broad ranges of stability. The optimal \({\zeta }_{{A}_{1}}\) was typically found to be in the range of 10−4–10−3 for s- and p-type Gaussians and 10−3–10−2 for d- and f-type Gaussians, whereas g-type Gaussian exponents usually had \({\zeta }_{{A}_{1}}={10}^{-1}\) (atomic units are assumed throughout unless otherwise specified). The optimal β ranges from 2.2 to 3.0 depending on the number of functions N in a given shell. Finally, to simultaneously describe the expulsion of the positron wavefunction from the nuclei, and accurately describe positron density maxima away from the molecule, we strategically place additional (H atom) aug-cc-pVXZ (X = T, Q) basis sets on ‘ghost’ centres close to the regions of maximum positron density. These additional Gaussians provide additional flexibility in the basis, enabling a better description of the positron wavefunction. In particular, they play an important role in enabling the accurate description of virtual-Ps formation, which occurs several atomic units away from the molecule, and which would require high angular momentum functions to resolve the electron–positron distance in Ps away if a single basis centre was used19. By placing Gaussian basis functions of angular momentum (we use l ≤ 4) on multiple ghost centres, higher angular momentum functions can be effectively generated in the interstitial regions (see appendix B of ref. 59 for details). In practice, for each molecule, we perform calculations with successively increasing number of ghost centres, whose locations are optimized manually until the binding energy stabilizes . The optimum locations are found iteratively: the calculation with zero ghosts generally indicates the region of maximum positron density, around which the ghosts are targeted in subsequent calculations, thus improving the density. As a general rule, we found that the optimal distance of the ghost centres from the atom closest to the maximum of positron density is about 1 Å. For some larger or nonpolar molecules, we use multiple ghost centres surrounding the molecule. To check convergence with respect to the number and location of these ghost centres, for each molecule we performed calculations including TZ or QZ bases on a successively increasing number of ghost centres in different arrangements until the increase in binding energy fell below a few per cent. We found that including ghosts can increase binding energies by ~10% in the polar molecules, and easily by ~30% for the nonpolar ones—for example, for CS2 we obtained εb = 39 meV at GW@BSE+Γ+Λ level with no ghosts, rising to εb = 68 meV with 16 additional ghosts. The use of higher angular momenta and more ghosts could be expected to further increase the binding energies of the nonpolar molecules. We also investigated the difference of using aug-cc-pVXZ for X = T, Q in the atomic-centred and ghost bases, and higher angular momenta in the even-tempered basis. Some improvement was noted moving from X = T to Q, and also when g states were included in addition to f, to a level of a 5%–10% in polar molecules, and 10%–30% in nonpolar molecules. Overall, good convergence with respect to both the electron and positron bases was observed (see for example, Extended Data Fig. 2).

The coefficients C in the expansion of the positron wavefunction in Gaussians are found by solving the Roothaan equations F±C± = S±C±ε±, where F± is the Fock matrix and S is the overlap matrix. The one-body and two-body Coulomb integrals of the Fock matrix are calculated using the McMurchie–Davidson algorithm60. We eliminate linearly dependent states by excluding eigenvalues <10−5 of the overlap matrices (typically ≲5% of the states). In practice, to minimize the basis dimensions we transform all quantities to a spherical harmonic Gaussian basis (for a given angular momentum, the number of Cartesian Gaussians is greater than or equal to the number of spherical harmonic Gaussians)61. Solution of the Roothaan equations yield bases of electron and positron Hartree–Fock molecular orbitals \(\{{\phi }_{\alpha }^{\pm }({\bf{r}})\}\) (which include ground and other negative energy states, and discretized continuum states) with which the self-energy diagrams can be constructed (see the next section for details).

Expanding the positron Dyson wavefunction in the positron Hartree–Fock molecular orbital basis as \({\psi }_{\varepsilon }({\bf{r}})={\sum }_{\nu }{D}_{{\rm{\nu }}}^{\varepsilon }{\phi }_{\nu }^{+}({\bf{r}})\) transforms the Dyson equation to the linear matrix equation HD = εD, where \(\langle {\nu }_{1}|H|{\nu }_{2}\rangle ={\varepsilon }_{{\nu }_{1}}{\delta }_{{\nu }_{1}{\nu }_{2}}+\langle {\nu }_{1}|{{\Sigma }}_{\varepsilon }|{\nu }_{2}\rangle \). Note that we calculate the full self-energy matrix including off-diagonal terms. Such a non-perturbative approach is essential for nonpolar molecules, where binding is enabled exclusively by correlations. In practice, to obtain the self-consistent solution to the Dyson equation, we calculate the self energy at a number of distinct energies Ei spanning the true binding energy εb, with the latter determined from the intersection of the εb(Ei) data with the line εb(E) = E.

The positron–molecule self energy

As discussed in the main text (Fig. 1), we consider three contributions to the irreducible self energy of the positron in the field of the molecule: ΣGW (which describes polarization, screening and electron–hole interactions); ΣΓ (which describes the non-perturbative process of virtual-Ps formation); and ΣΛ (which includes the infinite ladder series of positron–hole interactions). In practice, we construct the individual contributions by first solving the respective Bethe–Salpeter equations (BSE; see Extended Data Fig. 1) for the electron–hole polarization propagator Π, the two-particle positron–electron propagator \({G}_{{\rm{II}}}^{{\rm{ep}}}\) and the positron–hole two-‘particle’ propagator33 \({G}_{{\rm{II}}}^{{\rm{ph}}}\). Their general form is L(ω) = L(0)(ω) + L(0)(ω)KL(ω), where the L(0) are non-interacting two-body propagators and K are the interaction kernels33,62,63 (for example, see Extended Data Fig. 1e for the BSE for the electron–hole polarization propagator Π). In the excitation space of pair product Hartree–Fock orbitals L = (Cω − H)−1 = ξ(ω − Ω)−1ξ−1C −1, where the pair transition amplitudes ξ are the solutions of the pseudo-Hermitian linear-response generalized eigenvalue equations63,64,65 Hξ = CξΩ, ξ †Cξ = C, where

$$H=(\begin{array}{cc}A & B\\ {B}^{\ast } & {A}^{\ast }\end{array});\,\xi =(\begin{array}{cc}X & {Y}^{\ast }\\ Y & {X}^{\ast }\end{array});\,C=(\begin{array}{cc}1 & 0\\ 0 & -1\end{array});\,\Omega \,=\,(\begin{array}{cc}{\Omega }_{+} & 0\\ 0 & {\Omega }_{-}\end{array}),$$
(1)

for excitation energies \({{\Omega }}_{+}^{\alpha }\) and \({{\Omega }}_{-}^{\alpha }\), which are labelled by α = 1, …, dim(A). Here the A and B matrices depend on the particular two-particle propagator L under consideration and the approximation used for it (see Extended Data Table 4 for the explicit matrix elements): note that B = 0 for the two-particle propagators involving the positron, because the vacuum state for the diagrammatic expansion is that of the N-electron molecule, and thus there are no positron holes and only time-forward positron propagators. To determine the amplitudes, we use the parallel diagonalization algorithm of a previous work66, which exploits a similarity transform that gives the eigenvalues of C−1H as the square roots of the eigenvalues of (A + B)(A − B) (thus requiring matrices of dimension of the A block, that is, half of the full BSE matrix dimension) to obtain \(X=\frac{1}{2}({L}_{2}U+{L}_{1}V){{\Omega }}_{+}^{-1/2}\) and \(Y=\frac{1}{2}({L}_{2}U-{L}_{1}V){{\Omega }}_{+}^{-1/2}\), via the Cholesky decompositions \(A+B={L}_{1}{L}_{1}^{{\rm{T}}}\) and \(A-B={L}_{2}{L}_{2}^{{\rm{T}}}\), and the singular value decomposition \({L}_{2}{L}_{1}^{{\rm{T}}}=U{\Omega }{V}^{{\rm{T}}}\), where T indicates the transpose. The positron–molecule self-energy matrix elements can then be written as:

$$\langle {\nu }_{1}|{\Sigma }_{E}^{GW}|{\nu }_{2}\rangle =\sum _{\alpha ,{\nu }_{3}}\frac{{w}_{{\nu }_{1}{\nu }_{3}}^{\Pi ,\alpha }{w}_{{\nu }_{2}{\nu }_{3}}^{\Pi ,\alpha }}{E-{{\rm{\varepsilon }}}_{{\nu }_{3}}-{\Omega }_{+,\alpha }^{\Pi }+{\rm{i}}\eta },$$
(2)
$$\langle {\nu }_{1}|{\Sigma }_{E}^{\Gamma }|{\nu }_{2}\rangle =\sum _{\alpha ,n}\frac{{w}_{{\nu }_{1}n}^{\Gamma ,\alpha }{w}_{{\nu }_{2}n}^{\Gamma ,\alpha }}{E-{\Omega }_{\alpha }^{\Gamma }+{{\rm{\varepsilon }}}_{n}+{\rm{i}}\eta }-\langle {\nu }_{1}|{\Sigma }_{E}^{(2)}|{\nu }_{2}\rangle ,$$
(3)
$$\langle {\nu }_{1}|{\Sigma }_{E}^{\Lambda }|{\nu }_{2}\rangle =\sum _{\alpha ,\mu }\frac{{w}_{{\nu }_{1}\,\mu }^{\Lambda ,\alpha }{w}_{{\nu }_{2}\,\mu }^{\Lambda ,\alpha }}{E-{\Omega }_{\alpha }^{\Lambda }-{{\rm{\varepsilon }}}_{\mu }+{\rm{i}}\eta }-\langle {\nu }_{1}|{\Sigma }_{E}^{(2)}|{\nu }_{2}\rangle ,$$
(4)

where ν1, ν2 and ν3 denote positron indices and μ and n denote electron excited states and holes respectively, Σ(2)—which results from the Π(0) contribution to ΣGW and is present in both \({G}_{{\rm{II}}}^{{\rm{ep}}}\) and \({G}_{{\rm{II}}}^{{\rm{ph}}}\)—is subtracted to prevent double counting, and

$$\begin{array}{c}{w}_{{\nu }_{1}{\nu }_{3}}^{\Pi ,\alpha }=\sum _{\mu n}({\nu }_{1}{\nu }_{3}|\mu n)({X}_{\mu n}^{\Pi ,\alpha }+{Y}_{\mu n}^{\Pi ,\alpha }),\\ {w}_{{\nu }_{1}n}^{\Gamma ,\alpha }=\sum _{\mu {\nu }_{3}}({\nu }_{1}n|{\nu }_{3}\mu ){X}_{{\nu }_{3}\mu }^{\Gamma ,\alpha },\\ {w}_{{\nu }_{1}\mu }^{\Lambda ,\alpha }=\sum _{n{\nu }_{3}}({\nu }_{1}\mu |{\nu }_{3}n){X}_{{\nu }_{3}n}^{\Lambda ,\alpha },\end{array}$$
(5)

where chemists’ notation for Coulomb matrix elements (ν1ν3|μn) and so on is used (see Extended Data Table 4). The total self energy is calculated as Σ = ΣGW + ΣΓ + ΣΛ. Such addition of the individual channels is routine in atomic many-body theory calculations19,67,68 and in condensed matter, for example, the fluctuation-exchange (‘FLEX’) approximation69,70,71. We note that the above approach is restricted to molecules with ionization energies larger than the ground-state energy of Ps (6.8 eV). For these, the Ps-formation channel is closed, and Ps formation proceeds as a virtual process (with the electron temporarily tunnelling to the positron). For molecules for which the ionization is smaller than the energy of ground-state Ps, the inelastic Ps-formation channel is open. The above approach does not account for such inelastic channels. We note, however, that there are methods proposed to include inelastic channels in a many-body formalism38. Its implementation is beyond the scope of this paper, but would be a worthwhile future endeavour.

We implement the above in the massively parallelized EXCITON+ code developed by us, adapting the EXCITON code72,73,74 to include positrons. EXCITON employs density-fitting (of the electronic density) methods74,75,76,77,78,79 in a Gaussian-orbital basis for calculation of the electronic self-energy and four-centre integrals that appear in the A and B matrices of the BSE for finite73 and periodic72,74 systems. The EXCITON+ code developed at Queen’s University Belfast adapts EXCITON to additionally solve the positron–molecule Hartree–Fock problem, construct the full (nondiagonal) positron–molecule self energy (calculating wΠ, wΓ and wΛ via density fitting of the electronic density, and including screening terms in the ladders), and solve the Dyson equation and calculate the positron–electron contact density (lifetime with respect to annihilation). The use of density fitting reduces four-centre Coulomb integrals to products of three-centre Coulomb integrals and matrix elements of the Coulomb operator between atomic orbital basis functions. Thus, the memory scaling is approximately \({N}_{-}^{2}{M}_{-}\), where \({N}_{-}\) is the total number of electron basis functions, and \({M}_{-}\gtrsim 3{N}_{-}\) is the number of electron auxiliary basis functions. The most computationally demanding part of our approach is in the calculation of the virtual-Ps self-energy contribution ΣΓ. For this, dimA = dimXΓ = Nν × Nμ, the product of total number of positron molecular orbitals and excited electron molecular orbitals. For the calculations considered here, Nν ranged from 400–500 and Nμ from 300–400, resulting in dimXΓ = 120,000–200,000; thus, diagonalizing the matrix of (dimXΓ)2 elements demanded between ~100 GB and 1.5 TB of random access memory (RAM). The calculations were performed on two AMD EPYC 128 CPU @ 2 GHz, 768 GB RAM nodes of the United Kingdom Tier-2 supercomputer ‘Kelvin-2’ at Queen’s University Belfast. By contrast, the GW calculations involve dimA = dimXΠ ≤ Nν × Nn, that is, a maximum equal to the product of the number of occupied and excited electron molecular orbitals. In practice, not all occupied orbitals need to be included because the tightly bound lowest occupied molecular orbitals (LOMOs) are less susceptible to perturbation by the positron and have negligible contribution to the self energy. Thus, because Nn ≪ Nμ < Nν, ab initio GW@RPA/TDHF/BSE calculations (RPA, random phase approximation; TDHF, time-dependent Hartree–Fock; BSE, Bethe–Salpeter equation) are considerably less computationally expensive, and can be performed for molecules or clusters with ~100 atoms, providing at least lower bounds on the positron binding energies. Moreover, as discussed (see Fig. 3c and Extended Data Fig. 3) and demonstrated for nucleobases (Fig. 3d), the virtual-Ps formation contribution can be approximated by scaling the Σ(2) self energy by the strength parameter ratio \(g\equiv {{\mathscr{S}}}^{(2+{\Gamma })}/{{\mathscr{S}}}^{(2)}\), namely Σ ≈ gΣ(2) + ΣΛ, thus enabling computationally relatively inexpensive binding-energy calculations that account for virtual-Ps formation for molecules of ~100 atoms. Ab initio calculations for larger molecules including the virtual-Ps self energy will be feasible with additional computational resources, as would calculations using different truncated product spaces of excited electron and positron molecular orbitals and extrapolating to the basis set limit.

Improving the accuracy of calculations

As mentioned in the previous section, the computationally intensive calculations presented here were performed using relatively modest computational resources. Access to national supercomputing facilities would enable more complete basis sets and further exploration of the effect of ghost basis centres. Numerical accuracy can also be systematically improved in a number of ways. Exploiting the molecular point group symmetry via symmetry-adapted bases and using integral screening techniques would improve the efficiency of the calculations, enabling more complete basis sets to be used. This would ultimately improve the description of the correlations (particularly in generating higher angular momenta for improved description of the virtual-Ps formation process). The calculation of the positron–molecule self energy can be improved by implementing a self-consistent diagram approach in which the positron–molecule self energy is built from GW calculated electron and positron Dyson orbitals instead of Hartree–Fock ones33,80, and/or by coupling the three self-energy channels ΣGW, ΣΓ and ΣΛ by approximating the three-particle propagators via the Faddeev81, parquet69 or ADC(3)36 methods (expected to be computationally feasible for small molecules using national supercomputing facilities). Moreover, the diagrammatic series should be amenable to a diagrammatic Monte Carlo82,83 prescription, a powerful stochastic simulation method that enables the effective summation of many more (classes of) diagrams than considered here.

Positron annihilation rate in the bound state

The solution of the Dyson equation also yields the positron bound-state wavefunction ψε. Using it, the 2γ annihilation rate in the bound state \({\Gamma }={\rm{\pi }}{r}_{0}^{2}c{\delta }_{{\rm{ep}}}\) (Γ [ns−1] = 50.47δep [a.u.])—the inverse of which is the lifetime of the positron–molecule complex with respect to annihilation—can be calculated. Here r0 is the classical electron radius, c is the speed of light and δep is the electron–positron contact density,

$${\delta }_{{\rm{e}}{\rm{p}}}=\mathop{\sum }\limits_{n=1}^{{N}_{{\rm{e}}}}{\gamma }_{n}\int |{{\rm{\phi }}}_{n}({\bf{r}}){|}^{2}|{\psi }_{{\rm{\varepsilon }}}({\bf{r}}){|}^{2}{\rm{d}}{\bf{r}},$$
(6)

Here the sum is over all Ne occupied electron molecular orbitals with wavefunctions φn, and γn are molecular-orbital-dependent enhancement factors that account for the short-range electron–positron attraction20,84. Recent many-body calculations for atoms by one of us determined them to follow a physically motivated scaling with the ionization energy20,84 \({\gamma }_{n}=1+\sqrt{1.31/|{\varepsilon }_{n}|}+{(0.834/|{\varepsilon }_{n}|)}^{2.15}\) (where quantities are in a.u.), which we assume to hold here. The positron Dyson wavefunction is a quasiparticle wavefunction that is the overlap of the wavefunction of the N-electron ground state molecule with the fully correlated wavefunction of the positron plus N-electron molecule system33. It is normalized as

$$\int |{\psi }_{\varepsilon }({\bf{r}}){|}^{2}\,{\rm{d}}{\bf{r}}={(1-\partial \varepsilon /\partial E{|}_{{\varepsilon }_{{\rm{b}}}})}^{-1}\equiv a < 1,$$
(7)

which estimates the contribution of the ‘positron plus molecule in the ground state’ component to the positron–molecule bound-state wavefunction, that is, the degree to which the positron–molecule bound state is a single-particle state, with smaller values of a signifying a more strongly correlated state. Extended Data Figs. 4, 5 present contact density data. Extended Data Fig. 4a shows the individual molecular orbit contribution to the contact density as a function of the molecular orbit ionization energy. As in Fig. 3 (contribution of strength parameters from individual molecular orbits), overall the contact density increases as the ionization energy decreases: the positron overlap is greater with the more diffuse electronic HOMOs. However, molecular orbitals below the HOMO can in fact dominate, for example, acetonitrile, as shown further in Extended Data Fig. 5a–c, and Extended Data Fig. 6 for the primary nucleobases.