Abstract
Evolution is typically thought to proceed through divergence of genes, proteins and ultimately phenotypes1,2,3. However, similar traits might also evolve convergently in unrelated taxa owing to similar selection pressures4,5. Adaptive phenotypic convergence is widespread in nature, and recent results from several genes have suggested that this phenomenon is powerful enough to also drive recurrent evolution at the sequence level6,7,8,9. Where homoplasious substitutions do occur these have long been considered the result of neutral processes. However, recent studies have demonstrated that adaptive convergent sequence evolution can be detected in vertebrates using statistical methods that model parallel evolution9,10, although the extent to which sequence convergence between genera occurs across genomes is unknown. Here we analyse genomic sequence data in mammals that have independently evolved echolocation and show that convergence is not a rare process restricted to several loci but is instead widespread, continuously distributed and commonly driven by natural selection acting on a small number of sites per locus. Systematic analyses of convergent sequence evolution in 805,053 amino acids within 2,326 orthologous coding gene sequences compared across 22 mammals (including four newly sequenced bat genomes) revealed signatures consistent with convergence in nearly 200 loci. Strong and significant support for convergence among bats and the bottlenose dolphin was seen in numerous genes linked to hearing or deafness, consistent with an involvement in echolocation. Unexpectedly, we also found convergence in many genes linked to vision: the convergent signal of many sensory genes was robustly correlated with the strength of natural selection. This first attempt to detect genome-wide convergent sequence evolution across divergent taxa reveals the phenomenon to be much more pervasive than previously recognized.
Similar content being viewed by others
Main
Echolocation is a complex phenotypic trait that has evolved independently in bats and whales, and which involves the production, reception and auditory processing of ultrasonic pulses for obstacle avoidance, orientation and hunting11,12. Recent phylogenetic studies have shown that echolocating bats are not a true group—one lineage also contains the non-echolocating Old World fruit bats (family Pteropodidae), indicating that echolocation has evolved at least twice in bats, or was lost early in the evolution of Old World fruit bats13,14,15. New evidence supports the former scenario: divergent clades of echolocating bats seem to have undergone convergent amino acid replacements in several genes implicated in hearing8,16,17,18. Furthermore, some candidate hearing genes also show parallel changes in echolocating bats and whales, again suggesting roles in high-frequency hearing10,16,18,19. Other genes that might function in echolocation have been identified from screens for selection in bat20 and cetacean sequence data21. Here, using the evolution of echolocation as a model of phenotypic convergence, we investigated the extent to which parallel changes have occurred across the genome during the independent evolution of echolocation in bats and cetaceans.
We undertook genome sequencing of four divergent bat species, including both echolocating and non-echolocating forms. From the proposed suborder Yinpterochiroptera we sequenced the greater horseshoe bat Rhinolophus ferrumequinum and the greater false vampire bat Megaderma lyra, which exhibit ‘constant frequency’ (CF) and ‘frequency modulated’ (FM) echolocation, respectively (for details of calls, see refs 15, 22). From this suborder we also sequenced the non-echolocating straw-coloured fruit bat Eidolon helvum, to which we added published draft genome data from a second non-echolocating fruit bat, the large flying fox Pteropus vampyrus. From the second suborder, Yangochiroptera, we sequenced the CF echolocating Parnell’s moustached bat Pteronotus parnellii, and added published data from the FM echolocating little brown bat Myotis lucifugus.
For each of our four focal bat species, we generated paired-end short read sequence data on a Hi-Seq 2000 platform (Illumina), assembled the raw reads de novo into contigs using CLC bio, and then built scaffolds in SOAPdenovo (see Methods for details). Short-read data have been deposited into the Short Read Archive under accession numbers SRR924356, SRR924359, SRR924361 and SRR924427. We conducted homology-based gene prediction and identified 20,424 genes for R. ferrumequinum, 20,043 for M. lyra, 20,455 for E. helvum and 20,357 for P. parnellii. Screening for single-copy (1-to-1) orthologous protein-coding nuclear genes conserved across eutherian mammals identified 7,612 genes present in each of our four draft genomes (see Methods for details).
To build a mammal-wide alignment of orthologous coding gene sequences (CDSs) we retrieved the CDS of each locus from 18 published mammal genomes from Ensembl (http://www.ensembl.org/, release 63), covering a broad taxonomic range and including M. lucifugus and P. vampyrus (see Methods) as well as the echolocating common bottlenose dolphin Tursiops truncatus. Individual gene data sets were built and aligned in frame as codons with all ambiguous sites and codons removed (see Methods). To avoid potential errors that could arise either during sequencing or data assembly, which could adversely affect phylogenetic and molecular evolution analyses, we focused on all identified genes that, after clean up, contained no missing data or gaps in any of the newly sequenced bats. In total we generated alignments for 2,326 CDSs, each spanning at least 450 base pairs, and containing a minimum of six bat species (2% of alignments had missing data from P. vampyrus due to its lower coverage) as well as the bottlenose dolphin and the following five other mammals: dog Canis familiaris, horse Equus caballus, cow Bos taurus, mouse Mus musculus and human Homo sapiens.
To detect genome-wide sequence convergence between echolocating lineages, we built an analytical pipeline based on maximum likelihood (ML) phylogenetic reconstruction8,10,19. In this method, we examined each amino acid along the alignment of a given CDS, and measured its fit (site-wise log-likelihood support; SSLS) to the commonly accepted species tree23,24,25 (hereafter termed H0) and to two alternative topologies in which we forced echolocating taxa into erroneous monophyletic clades representing different convergence hypotheses (see Fig. 1a; for details see Supplementary Fig. 1 and Methods): H1 corresponds to all echolocating bats in a monophyletic group (‘bat–bat convergence’) and H2 to all echolocating mammals together in a monophyletic group (‘bat–dolphin convergence’). Using this approach we obtained the SSLS values of all amino acids under three different tree topologies. The difference in SSLS for a single site under the species tree and a given convergent tree with an identical substitution model denotes the relative support for the convergence hypothesis; for example, ΔSSLS (H1) = SSLS (H0) − SSLS (H1) (where negative ΔSSLS implies support for convergence; see Supplementary Fig. 2). We quantified the extent of sequence convergence at each locus by taking the mean of its ΔSSLS values, and found 824 loci with mean support for H1 and 392 for H2. Using simulations we confirmed that these convergent signals were not due to neutral processes and were robust to the substitution model used (see Supplementary Methods).
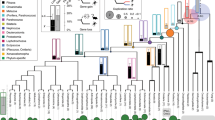
a, For each locus, the goodness-of-fit of three separate phylogenetic hypotheses was considered: (left) H0, the accepted species phylogeny based on recent findings (for example, refs 14, 23, 24, 25); (top-right panel) H1, or ‘bat–bat convergence’, in which echolocating bat lineages (shown in brown) are forced to form a monophyletic group to the exclusion of non-echolocating Old World fruit bats (shown in orange); and (bottom-right panel) H2, or ‘bat–dolphin convergence’, in which the echolocating bat lineages and the dolphin (blue) form a monophyletic group to the exclusion of all non-echolocating mammals. See Methods for details of model fitting and topologies. b, The distribution of convergence signal across 2,326 loci in 14–22 representative mammalian taxa, as measured by locus-wise mean site-specific likelihood support for the species topology (H0) over (left) the ‘bat–bat’ hypothesis uniting echolocating bats (that is, ΔSSLS (H1)) and (right) bat–dolphin hypothesis (that is, ΔSSLS (H2)). Representative hearing and vision loci are shown in green and blue, respectively; for each locus significance levels based on simulation denote whether it had significant counts of convergent sites after correcting for expected counts in random (control) phylogenies (*), and additionally whether strength of positive selection (dN/dS) and convergence (ΔSSLS) at sites under selection in echolocators were correlated (**); see Supplementary Table 4 and Methods.
We ranked the mean ΔSSLS for all 2,326 loci under both convergence hypotheses and, to assess the performance of our method, inspected the rank positions of seven hearing genes that have previously been shown to exhibit convergence and/or adaptation in echolocating mammals: prestin (Slc26a5), Tmc1, Kcnq4 (Kqt-4), Pjvk (Dfnb9), otoferlin, Pcdh15 and Cdh23 (see Methods). Prestin was ranked 43rd (H1) and 22nd (H2), whereas several other loci were also ranked highly in the distribution of convergence support values (see Fig. 1b). In addition to these, we also found several other hearing genes in the top 5% supporting H1 (Itm2b, Slc4a11) and H2 (Coch, Itm2b, Ercc3 and Opa1). Because bats and cetaceans are also known to have undergone shifts in spectral tuning and other adaptations in response to living in low light environments26,27,28, we also examined the position of genes implicated in vision and found four such loci in the top 5% of genes supporting H1 (Lcat, Slc45a2, Rabggtb and Rp1) and three supporting H2 (Jmjd6, Six and Rho; see examples in Fig. 1b and Supplementary Tables 2 and 3).
We tested statistically whether the strength of sequence convergence among echolocating bats, and between echolocating bats and the bottlenose dolphin, is greater in hearing genes than in other genes (for locus selection, see Methods). For each phylogenetic hypothesis, we averaged the mean ΔSSLS values of all 21 genes in our data set that are listed as linked to either hearing and/or deafness in any taxon based on published functional annotations (see Supplementary Information). By comparing our observed values to null distributions of corresponding values obtained by randomization, we found that hearing genes had significantly more negative average values than expected by chance for bat–dolphin convergence (H2: z = −0.0194, P < 0.05). We repeated this method for 75 genes listed as involved in vision and/or blindness, and found support, although weaker, in both cases of phenotypic convergence (z = −0.0020, P ≤ 0.055 and z = −0.0097, P ≤ 0.09). Loci previously reported to have association with echolocation had strong support by randomization for both hypotheses (P ≤ 0.01 in both cases).
We inspected direct protein–protein interactions among the 117 genes (top 5%) for H2 in networks of published interactions and found that 17 of these loci formed a single large network of direct interactions (for details see Supplementary Information and Supplementary Fig. 9) centred around Tp63 (p63) and Cdk1 (p34); p63 has been shown recently to be involved in cochlea development29 and Cdk1 has been shown to be important for development and regeneration of hair cells in the inner ear30. We also scanned databases of tissue-specific RNA expression in humans, finding some genes with elevated hypothalamus expression in human orthologues (Supplementary Information and Supplementary Table 13).
Most of the loci supporting the monophyly of echolocating bats, or the clade of echolocating bats plus dolphin, have no known roles in the sensory perception of sound or light. Yet given that many of these loci encode proteins with poorly characterized functions, a role in hearing or vision cannot be ruled out and in this respect it is noteworthy that highly ranked genes for H1 (top 5%) included five solute carrier proteins related to prestin, a motor protein that drives the cochlear amplifier8,19 (see Supplementary Table 2). Other loci that seem to support convergence among echolocating taxa can be more confidently ruled out as having roles in sensory perception; however, some of these loci may instead be associated with phenotypic traits that are correlated with aspects of echolocation.
Sequence convergence in loci related to shared phenotypic traits provides compelling but indirect evidence that genome-wide examples of convergence reported here are likely to be due to adaptive selection rather than neutral evolution. Analysis of the distribution of support for convergence within each locus indicated that mean support is driven by a few sites per locus (see Supplementary Information). For echolocating taxa under each convergent scenario, we directly estimated the strength of selection at each site as the ratio (omega, ω) of the rate of non-synonymous substitutions (dN) to the rate of synonymous substitutions (dS; ω > 1 being indicative of molecular adaptation; see Methods). To test whether site-wise support for a given hypothesis is driven by selection, we correlated absolute site-wise ΔSSLS and site-wise ω and found a strong relationship after correcting for locus identity (H1, P = 0.0336; H2, P < 0.001).
Previous work on prestin suggested that sequence convergence among echolocating taxa was a consequence of positive selection19. To determine the extent to which adaptive convergence occurs across the genome, for each locus we fitted the linear relationship between ΔSSLS and corresponding site-wise ω in echolocating lineages for those sites that show different selection pressures between echolocators and other taxa. We proposed that loci with sites undergoing diversifying selection for convergence (adaptive convergence) would exhibit a negative correlation, whereas those loci with sites undergoing divergence driven by diversifying selection, but under the accepted species topology (adaptive divergence), would exhibit a positive correlation. On the basis of whether the 95% confidence interval of the slope was below zero, for H1 we classified 92 loci as putatively adaptive convergent; conversely, in 111 loci, the 95% confidence interval of the slope was greater than zero, indicating adaptive divergence. Using the same approach for H2, we classified 59 loci as adaptive convergent and 212 loci as adaptive divergent (Fig. 2). The larger number of adaptive divergent loci seen under H2 reflects the stronger average relative support for H0 across the data set in H0H2 comparisons, as opposed to H0H1 comparisons; this is to be expected because H2 is a more radical rearrangement of the species phylogeny.
a, b, For hypotheses H1(a) and H2(b) (n = 2,030 and 1,876 loci, respectively), the 95% confidence intervals of the coefficient (slope) for locus-wise regressions between site-wise support for convergence and site-wise ω for sites under diversifying selection are plotted. In each plot, loci showing a negative relationship, as characterized by a slope significantly below zero, are consistent with an evolutionary trajectory of adaptive convergence (purple line, with filled circle indicating upper 95% limit) and loci showing a positive relationship, with a slope of greater than zero, are consistent with an evolutionary trajectory of adaptive divergence (orange line, with filled circle indicating lower 95% limit). Insets show two examples of adaptive convergence and divergence under each hypothesis. Full details of ω estimation and regression fitting are given in the Methods.
To explore more fully the relationship between signatures of convergence and adaptive evolution, we predicted the level of convergent evolution expected (ΔSSLS) after prolonged diversifying selection (ω = 2) using the fitted regression models for each locus. Genes associated with hearing and vision (including those encoding the solute carriers Slc44a2 and Slc4a11, associated with deafness, and the integrin Itgal, associated with blindness) showed significantly stronger convergence in these models than the background loci (see Supplementary Information). The genes identified in this analysis show a pattern of substitutions under differing selection regimes in echolocating and non-echolocating lineages that tend to have high ω and be convergent in echolocating lineages; we therefore suggest that sustained adaptive selection in these loci is likely to reinforce the signal for convergence as parallel changes accrue, in contrast to neutrally driven or adaptive divergence, which would tend to reinforce support for the species phylogeny over time.
Our genome-wide analysis shows that natural selection has acted on three echolocating lineages (cetaceans and two separate bat lineages) to produce a complex pattern of changes in protein sequence, including both divergent and, more surprisingly, extensive convergent changes. Many of these changes are in genes that may be associated with the shift in primary sensory modality (between vision and echolocation), either directly or through the associated complex changes in ecology and natural history. Furthermore, this work identifies clear targets for future experimental work, for instance tissue-specific RNA expression analyses. This study represents the first systematic attempt to provide a framework for the genomic analysis of sequence convergence associated with independently shared phenotypes. Our findings strongly suggest that, despite many recent papers reporting sequence convergence in particular candidate genes, the importance of this mode of molecular evolutionary change is relatively underappreciated, and is under-exploited in seeking to understand the genetic basis of complex traits such as echolocation.
Methods Summary
Taxonomic coverage, sequencing and assembly
Genome-wide short-read sequences (Hi-Seq, 500-bp inserts) were generated and assembled for one non-echolocating (Eidolon helvum) and three echolocating bats (Rhinolophus ferrumequinum, Megaderma lyra and Pteronotus parnellii). The former three belong to the suborder Yinpterochiroptera and the latter to the Yangochiroptera. A total of 7,612 coding sequences showed 1-to-1 orthology with Homo sequences and were present in all four taxa. Of these, 2,326 loci were aligned in MAFFT with published data from 17 additional taxa, including the non-echolocating bat Pteropus vampyrus, echolocating bat Myotis lucifugus and echolocating dolphin Tursiops truncatus.
Convergence pipeline
We built a pipeline to estimate the strength of natural selection (dN/dS ratio, ω) and support for convergence (ΔSSLS) for each amino acid by maximum likelihood. ω values were estimated using published software; ΔSSLS was calculated as the difference in fitted site-wise log-likelihoods under two competing hypotheses: a ‘null’ phylogenetic tree, reflecting the consensus species tree, and one of two ‘alternative’ phylogenies, in which either all echolocating bats, or all echolocating taxa (echolcating bats plus dolphin), were artificially forced into a monophyletic clade. Ancestral amino acid states were inferred using parsimony.
Null distributions
We compared observed ΔSSLS values to ΔSSLS estimated from (1) neutrally evolving amino acids simulated by Markov chain Monte Carlo mixture models (n ≥ 1,000); and (2) random ‘alternative’ topologies (n = 100).
Locus-wise adaptation/convergence regressions
For each locus the relationship between selection and convergence was modelled using least-squares regression. 95% confidence intervals were calculated for the line equation parameters. The fitted line equations were extrapolated to model the convergence signal under strong adaptive selection (ω = 2).
Hearing and vision genes
We used the gene ontology database DAVID (http://david.abcc.ncifcrf.gov) to identify which of our loci were putatively associated with hearing or vision. Simulation by randomization (n = 1,000) was used to compare the observed mean convergence values among these sensory loci to null distributions.
Online Methods
Taxonomic coverage
We collected new genome-wide sequence data from four bat species, selected from the two suborders and encompassing the paraphyly of echolocating bat lineages (see ref. 13). From the suborder Yinpterochiroptera we studied the non-echolocating Old World fruit bat Eidolon helvum (family Pteropodidae) and two laryngeal echolocating species, Megaderma lyra (Megadermatidae) and Rhinolophus ferrumequinum (Rhinolophidae). From the suborder Yangochiroptera we studied the laryngeal echolocating species Pteronotus parnellii (Mormoopidae) that has independently evolved constant frequency echolocation.
From Ensembl (http://www.ensembl.org/), we also obtained sequence data from two additional bats—the laryngeal echolocating species Myotis lucifugus (Yangochiroptera; Broad Institute) and the non-echolocating Old World fruit bat Pteropus vampyrus (Yinpterochiroptera; Baylor College of Medicine Human Genome Sequencing Center)—as well as the echolocating bottlenose dolphin Tursiops truncatus. Genomic sequences from 15 additional mammal species were downloaded from Ensembl giving a total of 22 mammals (listed in Supplementary Table 1).
Phylogenetic hypotheses tested
To investigate the prevalence of convergent evolution at a genome-wide level associated with the independent evolution of echolocation in bats and cetaceans, we used a method that builds on maximum-likelihood phylogenetic reconstruction. This method compares, for a given sequence alignment of orthologous coding sequences (CDS), the goodness-of-fit of the accepted phylogenetic tree with that of an alternative convergent hypothesis (in this case, in which echolocating taxa were forced into a spurious monophyletic clade). From our data set, we identified and tested three hypotheses: (1) H0, the commonly accepted species phylogeny (for example, refs 13, 23, 24, 25) in which cetaceans (represented in our data set by the common bottlenose dolphin Tursiops truncatus) are nested within the even-toed ungulates in the order Cetartiodactyla, and the order Chiroptera is split into the suborders Yangochiroptera and Yinpterochiroptera, with paraphyly of bat laryngeal echolocation13; (2) H1, or ‘bat–bat echolocation convergence’ (monophyly of all echolocating bats in the data set); and (3) H2, or ‘bat–dolphin convergence’ (monophyly of all echolocating mammals in the data set). All three phylogenetic hypotheses are shown in Fig. 1. The scale bar (in amino acid substitutions) is provided for approximate reference only, as branch lengths were optimized at runtime.
Because the H2 (bat–dolphin) hypothesis is necessarily a radical rearrangement of the commonly accepted species topology, and the concept of an ‘exact branching order’ or the ‘true’ topology does not apply in this case, we proposed a number of separate but related versions of this hypothesis, all of which were evaluated equally in the analysis. In each case the rest of the mammalian species phylogeny was fixed, as in the H1 hypothesis. In the first case we constrained all five echolocating taxa to a single ancestral node (‘hard polytomy’); second we enumerated the seven bifurcating trees that are possible where the position of T. truncatus is free to vary, but the suborders of echolocating bats—Yangochiroptera (P. parnellii and M. lucifugus) and Yinpterochiroptera (R. ferrumequinum and M. lyra)—were preserved. A final topology was specified as a soft polytomy, with the resolution of the clade of echolocators being resolved by RAxML at runtime, with the rest of the phylogeny remaining constrained. A majority clade-consensus (MCC) summary phylogeny was constructed from these 2,326 inferred soft-polytomy H2 trees using TreeAnnotator v1.7.4 (in the BEAST v1.7.4 distribution31). This phylogeny recovered the Yangochiroptera and Yinpterochiroptera clades of echolocating bats with good (>50%) node support. When we compared the goodness-of-fit of all phylogenies (as opposed to pairwise comparison relative to the species phylogeny Ho) we found the species phylogeny was preferred at 1,170 loci (55%), with the bat–bat phylogeny H1 preferred next most often (548 loci; 26%). The soft-polytomy version of H2 (resolved by RAxML) was the preferred phylogeny among 50% of the remaining loci, with remaining support equally split between the other H2 versions. We therefore adopted the soft polytomy, RAxML resolved version of H2 as our main bat–dolphin hypothesis.
Sequencing and data set assembly
Novel sequence data from the four bat species listed above were generated by BGI on an Illumina Genome Analyzer platform (Illumina), based on genomic libraries of 500-bp insert sizes. Using this method we obtained approximately 33–41 Gb of short read sequence data per species.
The CLC de novo algorithm (CLC bio) was used for assembling raw reads into contigs using different k-mer size values ranging from 32 to 50. The assembled contigs from the CLC output were then processed using the module Prepare of the SOAP package to do scaffold assembly using the scaff command of SOAPdenovo. Finally, gaps were filled using the GapCloser32 tool. The resulting assemblies consisted of between 210,080 and 315,526 genomic sequences (depending on species), with an average depth of coverage of 17× to 18×. Estimated genome size was approximately ∼2 Gb in all four bats, whereas contiguity (as assessed by the N50 statistic) ranged from 16,292 bp (M. lyra genomic sequences) to 27,140 bp (E. helvum). Homology-based gene prediction analyses using the genBlastG33 tool recovered 20,424 gene models for R. ferrumequinum, 20,043 for M. lyra, 20,455 for E. helvum and 20,357 for P. parnellii, in line with published gene content values for other mammals34. The completeness/contiguity of the gene representation was evaluated using the CEGMA (Core Eukaryotic Genes Mapping Approach) pipeline35,36 and found ranging across species between 61.29% to 77.02% and 90.32% to 96.77% for complete and partial genes, respectively. These compared well to the published M. lucifugus genome; when we analysed that genome using CEGMA the comparable completeness/contiguity scores for complete and partial genes were in the middle of this range (62.9% and 91.5%, respectively).
To identify genes adequate for systematic phylogenetic-based analyses of convergent sequence evolution, we next filtered the above predictions for single-copy orthologous protein-coding genes conserved across the Eutheria. This was achieved by performing reciprocal blast searches against a database consisting of the gene models for the four bats, and using as queries the human sequences of 11,185 genes reported as 1-to-1 or apparent 1-to-1 orthologues between the human and Myotis genomes in Ensembl databases (http://www.ensembl.org/, release 63). In total we determined 7,612 1-to-1 orthologous genes, from which the longest coding sequences (CDSs) were then retrieved from Ensembl for the 18 additional mammalian genomes (Supplementary Table 1).
CDS alignment
Coding gene sequences (CDS) of individual loci were built and aligned as codons using a modified version of transAlign37 incorporating MAFFT38, such that all sequences remained in the correct reading frame. Any ambiguously aligned sites, and codons with excessive numbers of gaps, were removed from each gene alignment using Gblocks39 under the following options: −t = c −b1 = “$b1” −b2 = “$b1” −b3 = 1 −b4 = 6 −b5 = h, where b1 = 70% of the sequences sampled in the data set.
In order to avoid potential biases due to either sequencing or assembly errors, for all phylogenetic and molecular evolution analyses, we chose to focus on only a subset of the identified genes. Specifically, we restricted our downstream analyses on data sets, which after filtering out of ambiguous sites showed no missing data in any of the sampled bats. The exception to this rule was P. vampyrus, which, because of its comparatively lower genome coverage, was missing in around 2% of CDS alignments. All final CDS alignments used in our analyses were characterized by a minimum length of 450 bp (or 150 codons/amino acids) and included a minimum of six bat species, the dolphin Tursiops truncatus and the additional following mammals as outgroups: Canis familiaris, Equus caballus, Bos taurus, Mus musculus and Homo sapiens. Of the 2,326 loci examined, 642 were also included in the analysis of ref. 20.
Sets of genes associated with hearing and vision
We interrogated our full CDS data set for loci that have been implicated in aspects of sensory perception of sound, including those that have been linked to deafness and/or ear development. For this we searched annotation databases hosted on the gene ontology (GO) site DAVID (http://david.abcc.ncifcrf.gov; ref. 40) and cross-referenced all of our CDSs with the terms ‘hearing’ or ‘deafness’. Using this approach, 23 ‘hearing loci’ were identified: TYR, SLC4A11, NECAP1, COCH, JAG1, HOXA1, GTF3C2, PROX1, GGA3, MKKS, SLC44A2, ITM2B, EDNRB, FBXO11, PI4KB, DISP1, ERCC3, HESX1, FZD6, BDNF, NF2, OPA1 and DFNB59. We refer to this set of genes as ‘hearing’.
We repeated annotation searches of our full set of CDSs for associations with vision, this time using the keywords ‘vision’ or ‘blindness’. In total, 75 loci were classified: PAX6, MED24, JMJD6, ATP6AP1, MCM2, TRAF4, GPC4, CIC, RDH8, IMPG2, CAD, RPGRIP1, HPS4, RABGGTA, RP2, CLN5, RPGRIP1L, VPS18, RP1, FZR1, GLI3, UNC119, GLRB, MYF5, COPZ1, MCM3, TTK, HMGCR, NPHP3, PDC, RPE65, PRPF3, ELOVL4, TGIF2, TCTN3, TGFBI, OPN4, ECD, NEUROD4, BBS2, PAICS, APC, LAMC1, SKIL, PDCL, RABGGTB, IFT172, BBS4, INTS7, LGSN, ZEB1, PELO, SMARCA5, KIT, CNNM4, GJD2, CCT3, RHO, RFC4, SLC45A2, VPS39, CTNNB1, STAT3, ADRA1B, GPRC5C, SP3, PRPF8, PVRL3, RRH, BCOR, SIX6, DRD1, NHS, TOPORS and LCAT. We refer to this set of genes as ‘vision’.
In addition, several loci associated with the sensory perception of sound have previously been reported as convergent for bat–bat or bat–whale echolocation in the literature: prestin19, KCNQ4 (KQT-4)17, Pcdh15, Cdh23 and otoferlin18, and Pjvk and Tmc1 (ref. 16). We downloaded the sequences published in these studies (including focal echolocating taxa and background sequences from other mammalian species as in Supplementary Table 1) from NCBI using the published accession numbers. We aligned each locus by MUSCLE41, and manually inspected them for quality. This included an initial phylogenetic step to check for long-branch effects where a de novo topology was estimated under ML (maximum likelihood) using RAxML (build 7.6.2; SSE3.MPI, compiled from source https://github.com/stamatak/standard-RAxML (refs 42, 43)) and the PROTCATDAYHOFF model of amino acid substitution. All seven loci were retained following this step and analysed alongside the automatically assembled CDS data sets. We refer to these manually assembled alignments as ‘published’.
Analysis pipeline
To detect signatures of molecular convergence in genomic data, we compiled an analysis pipeline consisting of previously released software for phylogenetic tree manipulation, phylogenetic reconstruction and codon model analyses in a Maximum Likelihood (ML) framework, as well as of a set of utility classes (available on request) for data handling, parsing and model/hypothesis testing. Our phylogenetic approach differs from genome-wide SNP comparisons for the detection of parallelism within intraspecific populations44, in that codons’ phylogenetic histories are evaluated and compared separately, but aggregated over each locus; we also use simulation to establish a reference null distribution for each locus, and compare observed convergence values for a given test phylogenetic hypothesis to an expected distribution derived from 100 additional phylogenies. This framework incorporates RAxML (build 7.6.2; SSE.MPI, compiled from source (https://github.com/stamatak/standard-RAxML (refs 42,43)) and a modified build of version 4.4b of PAML45; available on request) where input/output (I/O) functions were adjusted to facilitate parallel cluster implementation. The main algorithms remained unchanged and in testing gave identical output to that produced using executables distributed by the authors; available on request. All analyses were conducted on a mixture of 32- and 64-bit processors at the 3,000-node Queen Mary GridPP High Throughput Cluster hosted by the Physics Department at Queen Mary, University of London. Supplementary Fig. 1 gives a schematic representation of the pipeline workflow ((1) to (9) below).
Input (1): for each locus, the multiple sequence alignment was first filtered to remove ambiguous or incomplete codons, as well as premature stop codons. Gaps were retained. The alignment was also checked to determine how many of the 22 possible species were present, and any absent taxa were pruned from the species tree H0 and the convergence trees H1 and H2 using NewickUtilities46 (see Supplementary Fig. 1, panel (i)).
De novo phylogeny estimation (2): we generated a separate de novo phylogeny for each locus using RAxML 7.6.2 (refs 42,43) under the model PROTCATDAYHOFF in rapid-search mode and 10 separate random start trees. The de novo tree was used as an independent estimate of the tree length. ΔSSLS was subsequently calculated under this phylogeny as described below for H1 and H2 (see Supplementary Fig. 1, panel (ii)). The soft polytomy present in the H2 hypothesis (the four echolocating bats plus T. truncatus) was also resolved in a separate RAxML search using a constrained subtree, also under PROTCATDAYHOFF, in this step.
Model fitting (3): we fitted the checked alignment data to the H0, H1, H2 and de novo topologies using our modified build of the aaml program in PAML 4.4 (ref. 45) under the WAG + γ model with estimated amino acid frequencies. We also implemented the JONES and DAYHOFF models of amino acid substitution. However, topology comparison requires marginalization of the site likelihoods with respect to substitution model, so that competing phylogenies’ goodness-of-fit may be directly compared. Pilot studies of available alignments of orthologous coding sequences47 showed congruence in relative ΔSSLS estimates for each locus under different models of substitution (available on request). We also repeated our complete ΔSSLS analyses separately under JONES and DAYHOFF; the Pearson’s correlation coefficients between ΔSSLS values for WAG-JONES, WAG-DAYHOFF and JONES-DAYHOFF were 0.746, 0.979 and 0.742, respectively, for H0−H1; and 0.917, 0.892 and 0.981, respectively, for H0−H2.
We therefore determined to use the WAG model of substitution for all loci, optimizing model parameters separately for each locus; see Supplementary Fig. 1, panel (iii).
Convergence hypotheses fitting (4): the two hypothesized convergent phylogenies H1 and H2 were then fitted to the data as for the species tree H0 (Supplementary Fig. 1, panel (iv)). Because the data and the substitution models were the same, the difference in likelihood between two phylogenies reflects the strength of support for each in the data (see below).
Comparison of site-wise log-likelihood support (ΔSSLS) (5): we used the mean ΔSSLS of all sites in a locus as the primary measure of strength of support for convergence in this study. This statistic compares the goodness-of-fit of a pair of phylogenetic trees under a given model of evolution at every site in a DNA or amino acid alignment (see Supplementary Fig. 2). First the log-likelihood of the phylogeny (Supplementary Fig. 2a) and substitution model, given the data (Supplementary Fig. 2b), is calculated for every site in the alignment using ML (see above). Site-specific likelihood support, ΔSSLS, was then calculated:

where ΔSSLS for the ith site is given by the difference in log-likelihood units between the log-likelihood of the ith site under H0 (the species tree) and Ha (the alternative tree; one of H1 or H2). By this definition, sites with a better model fit to H0 (the species tree) will have a positive ΔSSLS, whereas sites with a better fit to the convergent topologies H1 or H2 will have a negative ΔSSLS (Supplementary Fig. 2c). The distribution of overall signal in the locus indicates the strength of support for convergence. In particular, loci with a negative mean ΔSSLS show net site-wise signal for convergence (Supplementary Fig. 2d). Boxplots showing the distribution of mean ΔSSLS by hypothesis are shown in Supplementary Fig. 3; the top 5% of loci by mean ΔSSLS for H1 and H2 are shown in Supplementary Tables 2 and 3, respectively (n = 805,053). As expected, mean ΔSSLS for the H1 and H2 hypotheses are positive, indicating that most sites in the data set are not convergent. Equally, mean ΔSSLS for the hypotheses defined by the de novo tree comparison is negative, indicating that the topology that was directly fitted to the data has slightly better goodness-of-fit in many cases.
To investigate the nature of the convergence signal at all sites across this genomic data set, we plotted the empirical cumulative distribution function of observed ΔSSLS for H1 and H2 for the site-wise data set (shown in Supplementary Figs 4 and 5, respectively). For both H1 and H2, 95% of the site-wise ΔSSLS observations were within ± 0.5 lnL units of the mean. However, some sites displayed large ΔSSLS observations: absolute log-likelihood ΔSSLS of >1 lnL unit were observed for 1,828 and 26,342 amino acids in H1 and H2, respectively. Furthermore, mean variance in site-wise convergence measured by locus was larger than the mean site-wise convergence measured across the whole data set. Together, these indicate that the distribution of ΔSSLS within a gene is aggregated; as the mean locus length in our data set is relatively short but with a large variance (mean number of amino acids 346.8; s.d. 242.4) this suggests that small numbers of large site-wise ΔSSLS may influence mean locus ΔSSLS disproportionately in short loci.
Simulation of expected site-wise ΔSSLS distribution (6): homoplasious amino acid replacements may arise by neutral processes and, therefore, we used simulation to determine whether site-wise convergence was more significant than expected by chance. For each locus, we generated an expected distribution of likelihood differences as follows: using Phylobayes 3.3f (ref. 48), we first used the ‘pb’ MCMC sampler to obtain the posterior distribution of substitution model parameters under the CAT GTR model, constraining the topology to the species (H0) tree. Each locus used one chain of 6,000 steps, sampling every 10 and discarding the first 1,000 as burn-in. We then used the ‘ppred’ function to simulate alignments using the model parameters from the samples in the stationary posterior distribution. Each simulated data set therefore contained identical numbers of sites and taxa to the observed alignment; and because we fitted a mixture model, sites’ heterogeneity parameters should reflect heterogeneity in the observed sequences. To generate an expected distribution, these replicates were analysed identically in the pipeline.
To determine how many replicates to use to form the expected distribution for each locus, we first simulated 50 alignments as described above from six loci that were representative of our data set in terms of alignment length, heterogeneity, ΔSSLS and tree length: ENSG00000008515, ENSG00000095906, ENSG00000121900, ENSG00000167671, ENSG00000170476 and ENSG00000173627. We calculated their site-wise ΔSSLS values in the pipeline and then compared a single randomlyselected replicate’s ΔSSLS distribution to that of a variable number of replicates’ pooled ΔSSLS values in a Kolmogorov–Smirnov test. Replicates (1 <n < 50) were sampled without replacement. Because the test’s D statistic measures the largest difference between the two distributions, it will correlate with the smoothness of their step functions. We determined that smoothness monotonically increased as more replicates were used to construct the reference distribution, with 20–30 replicates providing a reference distribution that was comparably smooth to that derived from 50 replicates (available on request); we repeated these analyses to calculate means and variances. A purely numerical simulation in R using more replicates (10,000) but ΔSSLS values simulated from a normal distribution parametized on the alignments’ ΔSSLS distribution’s means and variances gave a similar result (not shown).
Determining the significance of ΔSSLS signals (7): to ascribe confidence to our observed site-wise ΔSSLS measurements for the trees of interest, we followed a two-stage process. First, we measured the site-wise ΔSSLS for the tree comparison of interest H0 − Ha, described above. Next, we performed the same comparison on the simulated data sets, collated their ΔSSLS values and calculated their stepwise empirical cumulative density function (cdf), with linear interpolation. This allowed us to calculate the cumulative probability of the observed ΔSSLS under the null distribution. We define U, the unexpectedness of an observed site j’s ΔSSLS comparison of the species topology, H0 and an alternative topology Ha as:

Correction for expected U across random (control) phylogenies (8): the unexpectedness measure U quantifies the significance of a given site’s convergence signal, or more explicitly, the cumulative probability of the observed log-likelihood difference between the two topologies, given the species topology is correct. However, in cases where the species topology itself is distant from the maximally likely topology, or where the molecular signal is weak, ΔSSLS scores <0, indicating preference for the alternative topology, may arise spuriously. In this scenario, differential support for any alternative topology may be possible where the signal for the species topology is weak. To control for these cases, we generated 100 additional control phylogenies by resampling the H1 phylogeny taxon labels without replacement, obtained the mean site-wise U across this random set Ur, and calculated the controlled site-wise U, Uc as:

for each site j. These were summed across the locus and their arithmetic mean calculated. The random-tree controlled unexpectedness, Uc, therefore takes values on [−1, 1], where values greater than zero indicate that the observed ΔSSLS signal for the tree of interest, Ha, is both stronger than expected by chance assuming H0, and that cumulative probability is itself greater than that seen in random ΔSSLS comparisons.
We filtered loci with corrected unexpectedness Uc ≤ 0 from our principal gene lists (Figs 1 and 2, and Supplementary Tables 2 and 3); from our randomizations of hearing, vision and curated genes; from Metacore analysis; and from functional enrichment analyses.
Site-wise selection pressure
The ratio dN/dS or ω denotes the ratio of the rate of nucleotide substitutions that lead to a codon replacement (non-synonymous substitutions, dN) to the rate of nucleotide substitutions that do not change the coding sequence (synonymous substitutions, dS). Under the neutral model, dN and dS are expected to occur at approximately the same rate (ω ≈ 1), whereas sites constrained by purifying (negative) selection are expected to evolve with ω < 1, and those under diversifying (positive) selection with ω > 1. For each locus, we estimated ω across the phylogeny, and also in the clade of taxa hypothesized to be convergent, for every site in the data set using ML in our modified build of version 4.4b of the codeml program within PAML45.
The codon models M7 (the null model, with F3x4 frequencies, beta-distributed ω and 10 site categories) and M8 (site-wise selection, also beta-distributed ω with an additional ω category representing positive selection49) were fitted in our pipeline implementation of PAML 4.4b. The hypothesized phylogenies (H0, H1, H2) were fixed as the user tree and the models compared by likelihood ratio test (LRT). The individual LRTs’ P values were then corrected post-hoc in the complete data set for multiple tests using the method of Benjamini and Hochberg50. We then considered the site-wise ω estimate only from loci where the M8 model was favoured. In H1 and H2 comparisons, 2,235 and 2,234 loci (from the total set of 2,326) passed the LRT, respectively. The site-wise ω estimates (and their mean for each locus) derived from this method were compared to clade-specific ω estimates (see below, values available on request) and incorporated into the principal component analysis for site data (see below).
Clade-specific ω estimation and derived site-wise ω
Large ΔSSLS values might reflect true phylogenetic signal due to evolutionary divergence, or could alternatively arise from sequencing and/or alignment errors (such processing errors are addressed below).
Where ΔSSLS values represent phylogenetic signal this could be due to neutral drift or diversifying (adaptive) selection, in which case ΔSSLS should be proportional to site-wise ω. To test this we fitted the clade-specific Clade Model C (and null model M1a)51,52 and estimated ω on the H1 and H2 topologies for the hypothesized clade of echolocating taxa in each case. In this model, three separate ω ratios were estimated in the given convergent clade; ‘category 0’, denoted ω0, for sites under purifying selection where 0 < ω < 1; ‘category 1’, denoted ω1, for sites evolving neutrally, where ω≡ 1; and ‘category 2’, denoted ω2, for sites under diversifying selection, in which ω is free to take values >1. In this model, the three ω ratios are estimated by ML and the Bayes empirical Bayes (BEB) posterior probabilities that each site falls into category ω0, ω1 or ω2 calculated. For each site, the ω estimated in each category is then weighted by the BEB posterior probabilities and summed to give an estimate of site-wise ω (also see refs 16 and 19). In subsequent analyses we treated sites with a BEB posterior for the divergent site category 2 (ω2) of >0.5 as being under diversifying selection. As with the M8/M7 comparison above, we tested clade model C over the null (M1a) model by LRT, and the resulting complete set of P values were treated with a post-hoc correction following Benjamini and Hochberg50. We considered the site-wise clade-specific ω estimate only from loci where Model C was favoured.
We also examined the tree lengths for each CDS alignment under H0, H1 and H2; all were within the recommended limits for codon-based analyses, indicating that no large, long branches had biased the ML fitting/optimization.
Comparison of ancestral sequences with convergent taxa
Theoretically, signatures of sequence convergence might also arise under conditions of stronger purifying selection in echolocating taxa than in non-echolocating outgroups (for example, Old World fruit bats). However, ω in the fruit bats was not estimated directly, but instead was averaged over all non-echolocating taxa in the phylogeny. As a result, similar ω estimates in both the background clade and the foreground (convergent) clade could arise from unrelated divergence elsewhere in the phylogeny, instead of in the non-echolocating taxa. In such cases, the likelihood support for the monophyly of lineages of echolocating taxa could arise due to the presence of derived amino acid substitutions in the non-convergent outgroup with retention of shared ancestral states in taxa comprising the putative clade of echolocators; misinterpreted as convergence.
Therefore we reconstructed the amino acid sequences at the internal nodes of the H1 and H2 phylogenies for each locus using unweighted parsimony53. We then examined every position in the alignment, comparing the sequence at the most recent common ancestor (MRCA) of echolocating taxa with the sequences of extant echolocating taxa sampled at the tips themselves. Where two or more echolocating taxa shared a divergent substitution from the MRCA at the same position, we termed this a ‘parallel’ substitution. Comparing the counts of parallel substitutions with the ΔSSLS evidence for convergence at each locus, we found extremely good correspondence between the two measures; although 551 loci lacked any parallel substitutions for H1 (441 under H2) overall, only six of our 5% most convergent loci (n = 118) lacked parallel changes for H1 (seven in the most corresponding H2 comparison).
Spatial distribution of selected sites
Because it is known that estimated numbers of non-synonymous substitutions, and thus dN/dS ratios (ω), can be inflated by potential sequencing, annotation and alignment errors54, we performed analyses to assess the reliability of our selection results. Sequencing errors and misalignments (that is, continuous blocks of poorly aligned sites) will most commonly be characterized by spatially aggregated distributions of divergent amino acids (and hence correlations in the ω estimates of adjacent sites). We therefore diagnosed the spatial distribution of sites in each locus estimated to have undergone diversifying selection to look for this signal. Within each locus that had passed the LRT M8/M7 (site-wise selection), we identified those sites with a Bayes empirical Bayes posterior ≥ 0.5 (likely to belong to the divergent site class). We then calculated the intragenic distance as the interval in alignment position between each codon under diversifying selection. For this calculation, sequences were treated as circular such that the distribution of intragenic distances would be identical regardless of the location on the gene of any putative group of misaligned codons.
On the basis of this definition of intragenic distances, we developed four measurements of the aggregation of codons of interest along a locus. They were: the minimum distance between two codons; the range (max − min distance); the k distance (defined as the largest integer k such that no more than k + 1 intragenic distances were of length k); and the ‘exponent coefficient.’ The exponent coefficient assumes distances are exponentially distributed; the ranked distances are log-transformed and a linear regression fitted; this coefficient is the ‘exponent coefficient’. We fitted linear, generalized linear and generalized linear mixed models to see if these measures of intragenic aggregation correlated (with or without number of taxa or total CDS length) with ΔSSLS. Results of these analyses (available on request) showed that no CDSs were significant.
Principal component analysis
To explore broader patterns of association among signatures of convergence, selection and putative gene function, for both CDS (locus) and site-wise data, we undertook principal component analyses (PCA). Data were transformed to approximate a standard normal distribution. The PCA was repeated for H1 and for H2 with the mean and site-wise ΔSSLS (in CDS and site-wise analyses, respectively) measured with respect to H1 and H2. In the CDS data set we analysed the principal component weightings of mean ΔSSLS, number of taxa present, total amino acid count, count of amino acids with significant support (see ‘Simulation of expected site-wise ΔSSLS distribution’, above), mean ω (dN/dS) for sites in the divergent site class in the convergent clade (see clade-specific ω estimation and derived site-wise ω, above) and log-linear exponent coefficient (a measure of the spatial aggregation of positively selected sites, see ‘Spatial distribution of selected sites’, above). In the data set of all amino acids, we analysed the principal component weightings of site-specific likelihood support (ΔSSLS), number of taxa present, estimated ω (dN/dS; see site-wise selection pressure, above) and estimated ω in the convergent clade (see clade-specific ω estimation and derived site-wise ω, above). For the locus and site-wise analyses, variance was explained approximately equally across all components; example component loadings for the loci-based PCA of H1 and H2 are shown in Supplementary Fig. 7a, b, respectively. Example component loadings for the PCA of site-wise data in H1 and H2 are shown in Supplementary Fig. 8a, b, respectively.
Locus-wise adaptation/convergence regressions
High-magnitude ΔSSLS sites were positively correlated with estimated site-wise ω in the clade of echolocating mammals in both H1 and H2. A positive correlation was previously found between site-wise ω and ΔSSLS for the prestin gene19, that is, sites under stronger positive selection also showed larger ΔSSLS for the alternative (convergent) topology. To test whether site-wise support was driven by selection under each of the given convergent hypotheses, we fitted the following generalized linear mixed model, treating locus as a random effect:

where |ΔSSLS| is the absolute value of the site-specific log-likelihood support; α the line constant; β the regression coefficient; and ω2 is the clade-specific estimated site-wise ω (dN/dS rate ratio) for the divergent site class (site category 2) in the hypothetical clade of echolocating taxa (that is, the foreground clade of Clade Model C). For details, see ‘Clade-specific ω estimation and derived site-wise ω’, above. Owing to computational constraints arising from the size of the data set, we fitted the model above to replicate data sets directly subsampled without replacement from the original site-wise data set. For this, we jack-knifed 1,000 replicates, each containing 4,000 sites. Mean jack-knife estimates of the model parameters are given in Supplementary Table 5.
Modelling convergence
Several loci displayed significant regressions with a negative correlation between ω and ΔSSLS, and also showed support for convergence based on a negative mean ΔSSLS, but were not categorized as convergent in Fig. 2 because their ΔSSLS did not exceed the threshold we established above; that is, the value of the empirical cumulative density function (eCDF) of mean locus-wise ΔSSLS at the 5% significance level (thresholds were −0.01035 and −0.205 for H1 and H2, respectively). However, given their regression suggested a convergent evolutionary trajectory, we predicted the impact of continued selection on these loci by modelling the convergent signal following continued diversifying selection by estimating the ΔSSLS value at ω = 2 using the fitted linear relationship in each locus. We predicted two trajectories for each locus: an upper estimate of ΔSSLS incorporating the uncertainty in the regression parameter estimates (95% confidence intervals of the slope and the intercept); and a central estimate predicted from the mean slope and intercept. Loci were modelled as ‘convergent’ if the upper ΔSSLS estimate passed the ΔSSLS threshold and ‘possibly convergent’ if the upper estimate failed the ΔSSLS threshold, but the central estimate passed it.
‘Convergent’ (Supplementary Tables 6 and 7 for H1 and H2, respectively) or ‘possibly convergent’ predictions (top 50 loci are shown in Tables 8 and 9 for H1 and H2, respectively) were more common in the data sets of CDSs with a priori indicators for convergence (hearing, vision and published loci) than in randomly chosen loci. Predicted convergence signals were significantly stronger for vision loci compared to the background set in H1 (one-tailed T = −2.11; P ≤ 0.019 with ∼159 d.f.) and significantly stronger for hearing loci compared to the background set in H2 (one-tailed T = −2.23; P ≤ 0.016 with ∼41.7 d.f.).
Randomization analysis of convergence signal in hearing and vision genes
We analysed the strength of the signal for convergence, measured by mean ΔSSLS and by the number of sites per locus with significant site-wise ΔSSLS, under the H1 (bat–bat) and H2 (bat–dolphin) hypotheses among our manually curated subsets (see above) of loci that were associated with hearing (n = 23) or vision (n = 75), or previously reported (published) as convergent in the literature (n = 7). We measured the mean ΔSSLS and number of significantly convergent sites in each of these three subsets. To assess the significance of each result, we performed a randomization separately for each subset of loci as follows: 1,000 replicate data sets were simulated by reshuffling the observed values without replacement, and the expected mean ΔSSLS or number of significantly convergent sites for the subset of loci recomputed. The set of 10,000 expected mean values were taken together to form a null distribution; the position of the observed value in the empirical cumulative density function (eCDF) of the expected values is given as the significance, P. See Supplementary Tables 10 (H1) and 11 (H2).
Functional enrichment analysis
Having screened these genomes for convergence, we compiled lists of the most convergent (strongest ΔSSLS plus credible Uc, and alignment heterogeneity/signal: noise scores) loci in our data set. These genes represent prime candidates for molecular convergence, but direct experimental validation of their function has only been conducted in a handful of cases (for example, prestin, Tmc-1, Pcdh15). Because generating tissue-specific expression data for the relevant organs is fraught with difficulties (tropical bat cochleae are tiny, highly mineralized, and their storage in the field presents significant logistical challenges) we elected to analyse these target lists for functional enrichment in silico as an initial step towards inferring their function.
Functional enrichment analysis for all gene lists under investigation (top 5% of loci by signals for convergence in H1 and H2) was carried out using Fisher’s exact test and Benjamini–Hochberg50 correction. All enrichments were computed with respect to the background defined by the 2,204 loci under study, so as to avoid biases due to possible functional enrichments of the latter gene list. We thus investigated enrichment of our lists for Gene Ontology annotation terms55, KEGG pathways56, common interactors according to the HPRD database57, microRNA targets according to Targetscan58 and genes associated to human diseases according to the Genetic Association Database59.
At a Benjamini–Hochberg50 FDR of 30%, and retaining only functional categories represented by at least five genes in our H1 and H2 lists, only Gene Ontology annotations and microRNA targets showed significant enrichment. However, when a control gene list generated from ranked convergence signals of random phylogenies was used, approximately equivalent levels of enrichment were seen. The functional enrichment we found and present here should therefore be considered putative, and further work carried out to validate the functional roles of the loci with strongest evidence for convergence.
Overall, one significant enrichment was found for the top 5% most convergent H1 genes, pertaining to alcohol metabolic processes. For H2 lists, on the other hand, significant enrichments were found for several Gene Ontology categories and microRNA target sets. The comprehensive results obtained for both the functional enrichment analyses are collated in Supplementary Table 12 (117 loci representing the top 5% of loci by signal for H1 and H2).
Several loci with the most strongest signals for H2 convergence were found to be associated to the GO annotation ‘sensitivity to light stimuli’ (GO:0009416). Other categories enriched in the most convergent genes are related to vesicle-mediated transport, regulation of cell cycle and cell death.
We also compared our lists to sets of genes highly expressed (defined as reads per kilobase of transcript per million mapped reads (RPKM) >10) in human tissues according to the RNA-seq Atlas, and found the genes from the most convergent H2 list were enriched in genes highly expressed in the hypothalamus (P = 0.029, Fisher’s exact test; Supplementary Table 13).
We further analysed the most convergent genes from the H1 and H2 hypotheses, as well as those from random trees with weakest species tree support, using the Thompson Reuters Metacore database of interactions documented in the literature. For each list we extracted all networks in which the query convergence genes were directly connected (were adjacent vertices). A large network of 17 genes was discovered matching genes from the H2 list (see Supplementary Fig. 9), including TP63 (p63), CDK1 (p34) and several other genes. CDK1 (p34) has been reported to be closely involved in both regeneration and development of hair cells in the cochlea, a key cell cycle process required to replenish hair cell populations for efficient hearing30. Similarly, recent work suggests that p63 is involved in cochlear development29. Networks extracted from H1 and random tree query lists were much smaller, with a maximum of six loci present.
References
Soskine, M. & Tawfik, D. S. Mutational effects and the evolution of new protein functions. Nature Rev. Genet. 11, 572–582 (2010)
Clark, A. G. et al. Evolution of genes and genomes on the Drosophila phylogeny. Nature 450, 203–218 (2007)
Hughes, J. F. et al. Chimpanzee and human Y chromosomes are remarkably divergent in structure and gene content. Nature 463, 536–539 (2010)
Hoy, R. R. Evolution. Convergent evolution of hearing. Science 338, 894–895 (2012)
Grant, P. R., Grant, B. R., Markert, J. A., Keller, L. F. & Petren, K. Convergent evolution of Darwin’s finches caused by introgressive hybridization and selection. Evolution 58, 1588–1599 (2004)
Zhang, J. Z. & Kumar, S. Detection of convergent and parallel evolution at the amino acid sequence level. Mol. Biol. Evol. 14, 527–536 (1997)
Kriener, K., O’hUigin, C., Tichy, H. & Klein, J. Convergent evolution of major histocompatibility complex molecules in humans and New World monkeys. Immunogenetics 51, 169–178 (2000)
Li, G. et al. The hearing gene Prestin reunites echolocating bats. Proc. Natl Acad. Sci. USA 105, 13959–13964 (2008)
Castoe, T. A. et al. Evidence for an ancient adaptive episode of convergent molecular evolution. Proc. Natl Acad. Sci. USA 106, 8986–8991 (2009)
Liu, Y., Rossiter, S. J., Han, X., Cotton, J. A. & Zhang, S. Cetaceans on a molecular fast track to ultrasonic hearing. Curr. Biol. 20, 1834–1839 (2010)
Vater, M. & Kössl, M. in Echolocation in Bats and Dolphins (eds Thomas, J. T., Moss, C. F. & Vater, M. ) 89–98 (Univ. Chicago Press, 2004)
Au, W. W. L. & Simmons, J. A. Echolocation in dolphins and bats. Phys.Today 60, 40–45 (2007)
Teeling, E. C. et al. Microbat paraphyly and the convergent evolution of a key innovation in Old World rhinolophoid microbats. Proc. Natl Acad. Sci. USA 99, 1431–1436 (2002)
Teeling, E. C. et al. Molecular evidence regarding the origin of echolocation and flight in bats. Nature 403, 188–192 (2000)
Jones, G. & Holderied, M. W. Bat echolocation calls: adaptation and convergent evolution. Proc. R. Soc. B 274, 905–912 (2007)
Davies, K. T. J., Cotton, J. A., Kirwan, J. D., Teeling, E. C. & Rossiter, S. J. Parallel signatures of sequence evolution among hearing genes in echolocating mammals: an emerging model of genetic convergence. Heredity 108, 480–489 (2012)
Liu, Y. et al. The voltage-gated potassium channel subfamily KQT member 4 (KCNQ4) displays parallel evolution in echolocating bats. Mol. Biol. Evol. 29, 1441–1450 (2012)
Shen, Y.-Y., Liang, L., Li, G.-S., Murphy, R. W. & Zhang, Y.-P. Parallel evolution of auditory genes for echolocation in bats and toothed whales. PLoS Genet. 8, e1002788 (2012)
Liu, Y. et al. Convergent sequence evolution between echolocating bats and dolphins. Curr.Biol. 20, R53–R54 (2010)
Zhang, G. et al. Comparative analysis of bat genomes provides insight into the evolution of flight and immunity. Science 339, 456–460 (2013)
Sun, Y.-B. et al. Genome-wide scans for candidate genes involved in the aquatic adaptation of dolphins. Genome Biol. Evol. 5, 130–139 (2013)
Jones, G. & Teeling, E. C. The evolution of echolocation in bats. Trends Ecol. Evol. 21, 149–156 (2006)
Murphy, W. J., Pringle, T. H., Crider, T. A., Springer, M. S. & Miller, W. Using genomic data to unravel the root of the placental mammal phylogeny. Genome Res. 17, 413–421 (2007)
Lindblad-Toh, K. et al. A high-resolution map of human evolutionary constraint using 29 mammals. Nature 478, 476–482 (2011)
Zhou, X. et al. Phylogenomic analysis resolves the interordinal relationships and rapid diversification of the laurasiatherian mammals. Syst. Biol. 61, 150–164 (2012)
Zhao, H. B. et al. The evolution of color vision in nocturnal mammals. Proc. Natl Acad. Sci. USA 106, 8980–8985 (2009)
Zhao, H. B. et al. Rhodopsin molecular evolution in mammals inhabiting low light environments. PLoS ONE 4, e8326 (2009)
Fasick, J. I. & Robinson, P. R. Spectral-tuning mechanisms of marine mammal rhodopsins and correlations with foraging depth. Vis. Neurosci. 17, 781–788 (2000)
Terrinoni, A. et al. Role of p63 and the Notch pathway in cochlea development and sensorineural deafness. Proc. Natl. Acad. Sci. USA 110, 7300–7305 (2013)
Ryan, A. F. The cell cycle and the development and regeneration of hair cells. Curr. Top. Dev. Biol. 57, 449–466 (2003)
Drummond, A. J., Suchard, M. A., Xie, D. & Rambaut, A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol. Biol. Evol. 29, 1969–1973 (2012)
Li, R. et al. SOAP2: an improved ultrafast tool for short read alignment. Bioinformatics 25, 1966–1967 (2009)
She, R. et al. genBlastG: using BLAST searches to build homologous gene models. Bioinformatics 27, 2141–2143 (2011)
Kim, E. B. et al. Genome sequencing reveals insights into physiology and longevity of the naked mole rat. Nature 479, 223–227 (2011)
Parra, G., Bradnam, K. & Korf, I. CEGMA: a pipeline to accurately annotate core genes in eukaryotic genomes. Bioinformatics 23, 1061–1067 (2007)
Parra, G., Bradnam, K., Ning, Z., Keane, T. & Korf, I. Assessing the gene space in draft genomes. Nucleic Acids Res. 37, 289–297 (2009)
Bininda-Emonds, O. R. transAlign: using amino acids to facilitate the multiple alignment of protein-coding DNA sequences. BMC Bioinform. 6, 156 (2005)
Katoh, K., Kuma, K., Toh, H. & Miyata, T. MAFFT version 5: improvement in accuracy of multiple sequence alignment. Nucleic Acids Res. 33, 511–518 (2005)
Castresana, J. Selection of conserved blocks from multiple alignments for their use in phylogenetic analysis. Mol. Biol. Evol. 17, 540–552 (2000)
Huang da, W., Sherman, B. T. & Lempicki, R. A. Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nature Protocols 4, 44–57 (2009)
Edgar, R. C. MUSCLE: a multiple sequence alignment method with reduced time and space complexity. BMC Bioinform. 5, 113 (2004)
Stamatakis, A. RAxML-VI-HPC: maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics 22, 2688–2690 (2006)
Stamatakis, A. in Proceedings of 20th IEEE/ACM International Parallel and Distributed Processing Symposium (IPDPS2006) (High Performance Computational Biology Workshop, 2006)
Hancock, A. M. et al. Human adaptations to diet, subsistence, and ecoregion are due to subtle shifts in allele frequency. Proc. Natl Acad. Sci. USA 107, 8924–8930 (2010)
Yang, Z. PAML 4: phylogenetic analysis by maximum likelihood. Mol. Biol. Evol. 24, 1586–1591 (2007)
Junier, T. & Zdobnov, E. M. The Newick utilities: high-throughput phylogenetic tree processing in the UNIX shell. Bioinformatics 26, 1669–1670 (2010)
Ranwez, V. et al. OrthoMaM: a database of orthologous genomic markers for placental mammal phylogenetics. BMC Evol.Biol. 7, 241 (2007)
Lartillot, N., Lepage, T. & Blanquart, S. PhyloBayes 3: a Bayesian software package for phylogenetic reconstruction and molecular dating. Bioinformatics 25, 2286–2288 (2009)
Yang, Z., Nielsen, R., Goldman, N. & Pedersen, A. M. Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics 155, 431–449 (2000)
Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate—a practical and powerful approach to multiple testing. J. R. Stat. Soc. B. 57, 289–300 (1995)
Bielawski, J. P. & Yang, Z. H. A maximum likelihood method for detecting functional divergence at individual codon sites, with application to gene family evolution. J. Mol. Evol. 59, 121–132 (2004)
Wong, W. S., Yang, Z., Goldman, N. & Nielsen, R. Accuracy and power of statistical methods for detecting adaptive evolution in protein coding sequences and for identifying positively selected sites. Genetics 168, 1041–1051 (2004)
Fitch, W. M. & Margoliash, E. Construction of phylogenetic trees. Science 155, 279–284 (1967)
Schneider, A. et al. Estimates of positive Darwinian selection are inflated by errors in sequencing, annotation, and alignment. Genome Biol. Evol. 1, 114–118 (2009)
The Gene Ontology Consortium. Gene ontology: tool for the unification of biology. Nature Genet. 25, 25–29 (2000)
Kanehisa, M., Goto, S., Sato, Y., Furumichi, M. & Tanabe, M. KEGG for integration and interpretation of large-scale molecular datasets. Nucleic Acids Res. 40, D109–D114 (2012)
Prasad, T. S. K. et al. Human protein reference database - 2009 update. Nucleic Acids Res. 37, D767–D772 (2008)
Lewis, B. P., Burge, C. B. & Bartel, D. P. Conserved seed pairing, often flanked by adenosines, indicates that thousands of human genes are microRNA targets. Cell 120, 15–20 (2005)
Becker, K. G., Barnes, K. C., Bright, T. J. & Wang, S. A. The Genetic Association Database. Nature Genet. 36, 431–432 (2004)
Acknowledgements
We are grateful to K. Baker, L. Davalos, D. Hayman, E. Koilmani, Y. Liu, A. Peel, R. Ransome and A. Rodriguez for providing material for sequencing. We thank C. Walker (Queen Mary GridPP High Throughput Cluster) and A. Terry and C. Mein (Barts and the London Genome Centre) for providing access to computing facilities, and for assistance with running analyses. We are also grateful to S. Dodsworth, R. Buggs, K. Davies, J. Kirkpatrick, R. Nichols, Y. Wurm and S. Young for comments on the manuscript. This work was funded by Biotechnology and Biological Sciences Research grant BB/H017178/1 awarded to S.J.R., E.S. and J.A.C.
Author information
Authors and Affiliations
Contributions
S.J.R. conceived the study and secured funding together with J.A.C. and E.S. J.P. conducted all phylogenetic, convergence and selection analyses with input from S.J.R., G.T. and J.A.C. Processing and analyses of sequence data was undertaken by G.T., with input from E.S., who also conducted gene ontology analyses with P.P. Raw sequence data was generated under direction of Y.L. and S.J.R. The paper was written and figures prepared by J.P. and S.J.R. with input from G.T., J.A.C. and E.S.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Tables 1-13, Supplementary Figures 1- 9, Supplementary Methods and Supplementary References. (PDF 3222 kb)
PowerPoint slides
Rights and permissions
This work is licensed under a Creative Commons Attribution-Non-Commercial-ShareAlike 3.0 Unported licence. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-sa/3.0/.
About this article
Cite this article
Parker, J., Tsagkogeorga, G., Cotton, J. et al. Genome-wide signatures of convergent evolution in echolocating mammals. Nature 502, 228–231 (2013). https://doi.org/10.1038/nature12511
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature12511
This article is cited by
-
Patterns of enrichment and acceleration in evolutionary rates of promoters suggest a role of regulatory regions in cetacean gigantism
BMC Ecology and Evolution (2023)
-
Evolutionary dynamics of genome size and content during the adaptive radiation of Heliconiini butterflies
Nature Communications (2023)
-
The vocal apparatus: An understudied tool to reconstruct the evolutionary history of echolocation in bats?
Journal of Mammalian Evolution (2023)
-
Molecular mechanisms of adaptive evolution in wild animals and plants
Science China Life Sciences (2023)
-
Next Generation Sequencing Revolutionizes Organismal Biology Research in Bats
Journal of Molecular Evolution (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.