Abstract
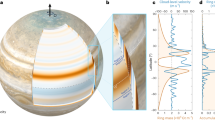
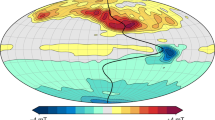
The observed cloud-level atmospheric circulation on the outer planets of the Solar System is dominated by strong east–west jet streams. The depth of these winds is a crucial unknown in constraining their overall dynamics, energetics and internal structures. There are two approaches to explaining the existence of these strong winds. The first suggests that the jets are driven by shallow atmospheric processes near the surface1,2,3, whereas the second suggests that the atmospheric dynamics extend deeply into the planetary interiors4,5. Here we report that on Uranus and Neptune the depth of the atmospheric dynamics can be revealed by the planets’ respective gravity fields. We show that the measured fourth-order gravity harmonic, J4, constrains the dynamics to the outermost 0.15 per cent of the total mass of Uranus and the outermost 0.2 per cent of the total mass of Neptune. This provides a stronger limit to the depth of the dynamical atmosphere than previously suggested6, and shows that the dynamics are confined to a thin weather layer no more than about 1,000 kilometres deep on both planets.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

 over a wide range of interior models for Neptune.
over a wide range of interior models for Neptune.

 as function of the decay height H for Uranus and Neptune.
as function of the decay height H for Uranus and Neptune.
Similar content being viewed by others
References
Read, P. L. Clearer circulation on Uranus. Nature 325, 197–198 (1987)
Lian, Y. & Showman, A. P. Generation of equatorial jets by large-scale latent heating on the giant planets. Icarus 207, 373–393 (2010)
Liu, J. & Schneider, T. Mechanisms of jet formation on the giant planets. J. Atmos. Sci. 67, 3652–3672 (2010)
Suomi, V. E., Limaye, S. S. & Johnson, D. R. High winds of Neptune — a possible mechanism. Science 251, 929–932 (1991)
Aurnou, J., Heimpel, M. & Wicht, J. The effects of vigorous mixing in a convective model of zonal flow on the ice giants. Icarus 190, 110–126 (2007)
Hubbard, W. B. et al. Interior structure of Neptune — comparison with Uranus. Science 253, 648–651 (1991)
Hubbard, W. B. Gravitational signature of Jupiter’s deep zonal flows. Icarus 137, 357–359 (1999)
Kaspi, Y., Hubbard, W. B., Showman, A. P. & Flierl, G. R. Gravitational signature of Jupiter’s internal dynamics. Geophys. Res. Lett. 37 L01204 (2010)
Kong, D., Zhang, K. & Schubert, G. On the variation of zonal gravity coefficients of a giant planet caused by its deep zonal flows. Astrophys. J. 748, 143 (2012)
Kaspi, Y. Inferring the depth of the zonal jets on Jupiter and Saturn from odd gravity harmonics. Geophys. Res. Lett. 40, 676–680 (2013)
Hubbard, W. B. Planetary Interiors (Van Nostrand Reinhold, 1984)
Zharkov, V. N. & Trubitsyn, V. P. Physics of Planetary Interiors (Pachart Publishing House, 1978)
Helled, R., Anderson, J. D., Podolak, M. & Schubert, G. Interior models of Uranus and Neptune. Astrophys. J. 726, 15 (2011)
Jacobson, R. A. The gravity field of the Uranian system and the orbits of the Uranian satellites and rings. Bull. Am. Astron. Soc. 39 (3). 453–453 (2007)
Jacobson, R. A. The orbits of the Neptunian satellites and the orientation of the pole of Neptune. Astrophys. J. 137, 4322–4329 (2009)
Hubbard, W. B. & Marley, M. S. Optimized Jupiter, Saturn, and Uranus interior models. Icarus 78, 102–118 (1989)
Podolak, M., Weizman, A. & Marley, M. Comparative models of Uranus and Neptune. Planet. Space Sci. 43, 1517–1522 (1995)
Fortney, J. J. & Nettelmann, N. The interior structure, composition, and evolution of giant planets. Space Sci. Rev. 152, 423–447 (2010)
Nettelmann, N., Helled, R., Fortney, J. J. & Redmer, R. New indication for a dichotomy in the interior structure of Uranus and Neptune from the application of modified shape and rotation data. Planet. Space Sci. 77, 143–151 (2013)
Kaspi, Y., Flierl, G. R. & Showman, A. P. The deep wind structure of the giant planets: results from an anelastic general circulation model. Icarus 202, 525–542 (2009)
Schneider, T. & Liu, J. Formation of jets and equatorial superrotation on Jupiter. J. Atmos. Sci. 66, 579–601 (2009)
Liu, J., Goldreich, P. M. & Stevenson, D. J. Constraints on deep-seated zonal winds inside Jupiter and Saturn. Icarus 196, 653–664 (2008)
Pedlosky, J. Geophysical Fluid Dynamics (Spinger, 1987)
Pearl, J. C. & Conrath, B. J. The albedo, effective temperature, and energy balance of Neptune, as determined from Voyager data. J. Geophys. Res. 96, 18921–18930 (1991)
Helled, R., Anderson, J. D. & Schubert, G. Uranus and Neptune: shape and rotation. Icarus 210, 446–454 (2010)
Karkoschka, E. Neptune’s rotational period suggested by the extraordinary stability of two features. Icarus 215, 439–448 (2011)
Hammel, H. B., de Pater, I., Gibbard, S., Lockwood, G. W. & Rages, K. Uranus in 2003: zonal winds, banded structure, and discrete features. Icarus 175, 534–545 (2005)
Sromovsky, L. A. & Fry, P. M. Dynamics of cloud features on Uranus. Icarus 179, 459–484 (2005)
Sromovsky, L. A., Limaye, S. S. & Fry, P. M. Dynamics of Neptune’s major cloud features. Icarus 105, 110–141 (1993)
Sromovsky, L. A., Fry, P. M., Dowling, T. E., Baines, K. H. & Limaye, S. S. Neptune’s atmospheric circulation and cloud morphology: changes revealed by 1998 HST imaging. Icarus 150, 244–260 (2001)
Acknowledgements
Y.K. and O.A. thank the Helen Kimmel Center for Planetary Science at the Weizmann Institute of Science for support. A.P.S. and W.B.H. acknowledge support by NASA.
Author information
Authors and Affiliations
Contributions
Y.K. and A.P.S. initiated and designed the research. Y.K. performed the dynamical gravity harmonics calculations and wrote the paper. R.H. performed the static interior model calculations and their interpretation. All authors contributed to the discussion of the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data 1-2, Supplementary Table 1, Supplementary Figure 1 and additional references. (PDF 228 kb)
Rights and permissions
About this article
Cite this article
Kaspi, Y., Showman, A., Hubbard, W. et al. Atmospheric confinement of jet streams on Uranus and Neptune. Nature 497, 344–347 (2013). https://doi.org/10.1038/nature12131
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature12131
This article is cited by
-
Atmospheric Science Questions for a Uranian Probe
Space Science Reviews (2024)
-
Thermal and Tidal Evolution of Ice Giants with Growing Frozen Cores: The Case of Neptune
Space Science Reviews (2024)
-
Uranus and Neptune are key to understand planets with hydrogen atmospheres
Experimental Astronomy (2022)
-
Ice giant system exploration within ESA’s Voyage 2050
Experimental Astronomy (2022)
-
In Situ exploration of the giant planets
Experimental Astronomy (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.