Main

Many transport processes are induced by the existence of local gradients of some entity such as chemical potential, temperature or concentration. Gradients will also naturally generate, or influence, flows in complex networks. For example, in the case of information networks, properties of the nodes (such as rate of processing and adequacy) will generate a bias (formulated as a gradient criterion) in the way information is transmitted from a node to its neighbours. Specific examples include the World Wide Web, distributed computing4 and social networks with competitive dynamics5.

A simple model of a transport process begins by assuming that there are N nodes whose connections are described by a fixed substrate network, S. Associated with each node i is a non-degenerate scalar, hi, which describes the ‘potential’ of the node. Then the gradient network can be constructed as the collection of directed links pointing from each node to whichever of its near-neighbours on S or itself has the highest potential. It can be shown that all non-degenerate gradient networks are forests — that is, they have no loops (except for self-loops) and consist only of trees. Furthermore, if S is a simple random graph3, in which each pair of nodes is linked with probability P, and the scalars hi are independent identically distributed random variables, then the distribution of the number of links pointing to each node (the in-degree distribution) becomes (equation (1); derivation to be published elsewhere)

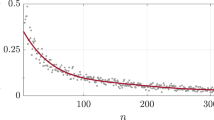
In the limit N→∞ and P→0, such that the average degree z≡NP=constant≫1, the exact degree distribution (equation (1)) becomes the power law R(l)≈l−1, with a finite-size cut-off at lc=z (Fig. 1a). In this limit, therefore, gradient networks are scale-free. This is surprising6 because the substrate S is not scale-free, and in the same limit it has a ‘bell-curve’ degree distribution. Alternatively, if the substrate network S is scale-free, as in a Barabási–Albert network1, then the associated gradient network is also scale-free (Fig. 1b) and is characterized by the same exponent.

Figure 1: Degree distributions of gradient networks and jamming.
figure 1

a, Comparison between the exact formula (equation (1), green line) and numerical simulations (ellipses). Here N=1,000, P=0.1 (z=100); slope (dashed red line) is −1. b, Degree distributions of the gradient network and the substrate, when the substrate is a Barabási–Albert scale-free graph with parameter m (for m=1, in black: R(l), circles; P(k), full line. For m=3, in purple: R(l), diamonds; P(k), dashed line); N=105. c, Jamming coefficient J for random graphs (circles, P=0.05; diamonds, P=0.1; orange line, P=0.05, exact expression; red line, P=0.1, exact expression) and scale-free networks (pink, m=1; green, m=3). Each data point is the average of 104 runs in a and 103 runs in b.

Full size image

For a network S, where the flow is processed at nodes in a finite time (such as in the routing of a packet), the quality of flow processing can be quantified by considering the jamming or congestion factor, which is defined as (equation (2))

where Nreceive is the number of nodes that receive gradient flow and Nsend is the number of nodes that send it. Note that J is a queuing characteristic, rather than an actual throughput measure. Certainly, 0≤J≤1, with J=1 corresponding to maximal congestion (vanishing number of receivers/processors) and J=0 to no congestion. For a random substrate network, the expression of J simply follows from equations (1) and (2) which, in the large network scaling limit, where P is constant and N → ∞, becomes

where O(1/N) indicates corrections of order 1/N.

Random networks therefore become maximally congested in that limit. For scale-free networks, however, the conclusion in the same limit is drastically different. In that case, J tends to a positive constant bounded away from unity — that is, scale-free networks are not prone to jamming. Figure 1c compares the congestion as a function of N for both random and scale-free substrate networks.