Main

Like Gaspard et al.1, we have analysed the position of a single particle colliding with many others. We used the Ehrenfest wind-tree model3, in which the point-like (‘wind’) particle moves in a plane, colliding with randomly placed, fixed square scatterers (‘trees’) (Fig. 1a). We chose this model because collisions with the flat sides of the squares do not lead to exponential separation of corresponding points on initially nearby trajectories, so there are no positive Lyapunov exponents, which are characteristic of microscopic chaos. In contrast, Gaspard et al.1 used a Lorentz model as being similar to brownian motion, a model in which the squares are replaced by hard, circular discs. This does exhibit exponential separation of nearby trajectories, leading to a positive Lyapunov exponent and hence microscopic chaos.

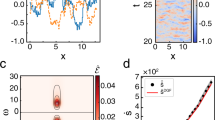
Figure 1: Brownian motion results of Gaspard et al.1 numerically reproduced from the non-chaotic Ehrenfest wind-tree model (notation as in ref. 1).
figure 1

The square scatterers have a diagonal of two length units and fill half the area considered. The particle moves with unit velocity in four possible directions. The position on its trajectory is determined for 106 points separated by one time unit. a, Two nearby trajectories split only at a corner C; no exponential separation occurs (see Fig. 1 of ref. 1). b, A typical trajectory is diffusive with an ω−2 power spectrum (inset), where ω is the angular frequency (see Fig. 2 of ref. 1). c, The information entropy K(n, ε, τ) for τ=1 and ε=0.316×1.21m, where m is an integer running from 0 to 25 (see Fig. 3 of ref. 1). d, The envelope of the slopes of these K curves, h(ε,τ) appears to imply a positive (chaotic) hKS for the Ehrenfest model, as for brownian motion (see Fig. 4 of ref. 1).

Full size image

Nevertheless, despite being non-chaotic, the Ehrenfest model reproduces all the results presented by Gaspard et al.1. The particle trajectory segment shown in Fig. 1b is strikingly similar to that for the brownian particle (Fig. 2 of Gaspard et al.). Our subsequent analysis parallels that of Gaspard et al.1, where further details may be found.

The microscopic ‘chaoticity’ is determined by estimating the Kolmogorov–Sinai entropy hKS as described4,5 by using the information entropy K(n, ε, τ) obtained from the frequency with which the particle retraces part of its (previous) trajectory within a distance ε, for n measurements spaced at a time interval τ. As hKS here equals the sum of the positive Lyapunov exponents, the determination of a positive hKS would imply microscopic chaos. Like Gaspard et al.1, we find that K grows linearly with time (Fig. 1c), giving a positive (non-zero) bound on hKS (Fig. 1d). Indeed, Fig. 1b–d for a microscopically non-chaotic model are virtually identical to the corresponding Figs 2–4 of Gaspard et al. Thus, Gaspard et al. did not prove the presence of microscopic chaos in brownian motion.

The algorithm of refs 4,5 as applied here cannot determine the microscopic chaoticity of brownian motion because the time interval between measurements, 1/60 s (ref. 1), is so much larger than the microscopic timescale determined by the inverse collision frequency in a liquid, which is approximately 10−12s. A decisive determination of microscopic chaos would require a time interval τ of the same order as characteristic microscopic timescales.