Introduction

Gaussian beams, which are characterized by a transverse Gaussian intensity profile, are the most commonly used beams in laser optics. However, there are many other types of structured beams1, representing different solutions of the underlying wave equation for light in free-space—the Helmholtz equation—that maintain, in general, their shape during propagation. Such beams include the Hermite–Gauss (HG) beams, having multiple intensity lobes, Laguerre–Gauss vortex beams that are characterized by helical phase and carry orbital angular momentum (OAM)2, 3, self-accelerating Airy beams that propagate along parabolic caustic trajectories4 and more5. There are numerous applications that utilize these structured beams, for example, their linear momentum applies a reaction force that can trap particles, whereas the angular momentum, for example, of vortex beams, can be used for rotating them1, 6, 7, 8, 9, 10. Vortex beams are also useful for depleting fluorescent dye molecules in stimulated emission depletion (STED) microscopy11, while Airy beams can be used for optically mediated particle clearing12 and light sheet microscopy13. Until recently, all the realizations of structured beams were limited in scale by the standard diffraction limit λ/2NA (where λ is the optical wavelength and NA is the lens numerical aperture). This limit originates from the beam size for a lens illuminated by a plane wave, and is also identical to the Abbe resolution limit14. However, when the lens is not homogenously illuminated, smaller features can be obtained at the focal plane. Already, in 1872 J W Strutt, also known as Lord Rayleigh has demonstrated that a smaller spot of 0.36λ/NA is achievable by modulating the input beam using an annular aperture15. Later G T Di Francia16 proposed the concept of super-directive antennas could be applied to optical instrument to achieve the much narrower focal spot than the Abbe limit. By following the concepts that were developed for weak quantum mechanical measurements17, Michael Berry introduced the concept of super-oscillations for the band-limited functions that locally oscillate faster than their highest Fourier component18. The phenomenon of super-oscillations, exploited in the form of super-oscillatory lens in optical microscopy, was proposed as a method to achieve super-resolution imaging19, 20. In this case, since the lens generates a band-limited intensity pattern with a bandwidth of 2NA/λ, a light field locally oscillates faster than that is super-oscillatory. Indeed, super-oscillating (SO) beams with sub-diffraction limit features (but without any internal structure) have been demonstrated by modulating the lens pupil21, 22 and by superposition of Bessel beams23, 24, 25. A question that arises is whether it is possible to structure these sub-wavelength light spots. If so, exciting new possibilities will emerge for particle manipulation26, 27 and super-resolution microscopy beyond the diffraction limit.

In this paper, we present a systematic approach for structuring SO beams. We note that a different approach was proposed in Ref. 24, but was not explored experimentally up till now. Here we demonstrate our method by realizing SO beams with features that are smaller than half of the optical wavelength and having either multiple lobes, or a helical phase-front or an Airy-like shape. In order to demonstrate the usefulness of these beams, we utilize them to trap a single nano-particle with unprecedented localization and stiffness using an SO-Gaussian beam with a single-central lobe. In addition, we use multi-lobe SO-Gaussian beams to trap multiple nano-particles and SO-vortex beams to rotate particles clockwise and counter-clockwise at different angular velocities.

Materials and methods

Mask realization

To introduce our approach to the realization of structured SO beams, let us first consider the case in which at the pupil plane of the lens an annular phase mask is inserted, consisting of two regions with opposite phase. The mask is expressed by Refs. 28, 29:

where 0<rπ<rmax, rmax=D/2, D is the diameter of the mask aperture at the pupil plane and r is the radial co-ordinate. Plane wave illumination of this binary phase mask will generate the Fourier transform at the focal plane of the lens. This generated beam is a super-oscillatory beam, having a central lobe whose size is determined by rπ, followed by a peripheral ring of light. To experimentally realize the super-oscillatory structured beams, we implemented this binary mask into an off-axis computer-generated hologram30. The carrier wave number kc of the hologram determines the separation of the unwanted zero order and the target SO beams in first order, using the following phase modulation pattern:

Where is the phase function of the Fourier transform of the desired super-oscillatory structured beams. The advantage of this method is that both the amplitude and phase of the wave functions can be realized in the first order of the diffraction pattern by modulating only the phase of the beam, hence it can be easily realized with a spatial light modulator. By changing rπ the focal spot size of the SO beams can be made arbitrarily small, although the spot intensity is simultaneously reduced. In the Supplementary Materials, we provide a numerical comparison of the local frequencies of an SO beam and a normal Bessel beam that is obtained from a circular aperture. We also show the variation of focal spot size of SO beam as a function of rπ.

Experimental details

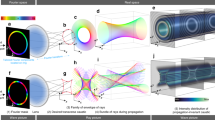
We implement Equation (2) by encoding it onto a phase-only spatial light modulator (SLM). The SLM has 800 × 600 pixels with pixel pitch 20 μm used in the reflective mode. A spatially filtered and collimated linearly polarized Gaussian laser beam (Coherent, Verdi 6) at λ=532 nm is incident on the SLM. The reflected wave-fronts from the SLM, with the help of the telescopic lenses and dichroic mirror reached to the back aperture of 100 × oil-immersion microscope objective (MO) lens with NA=1.4 (Olympus IX-71 microscope, Tokyo, Japan). In the focal volume of MO, the desired profiles of the structured SO beams having the sub-diffraction focal spots are realized, as shown in Figure 1a. Different experimental realizations of three-dimensional (3D) intensity distribution of the structured SO beams calculated according to Equation (2) are presented in Figure 1b–1e using the volumetric imaging technique31, that is, reconstruction from two-dimensional (2D) sections taken by imaging the beam as reflected from a mirror in the image plane. We characterize the size of our diffraction limited beam from the full-width half maximum (FWHM) of its reflection from a mirror placed in the sample plane. The parameters of SO-Gaussian beam, SO-vortex beam, SO-HG beam and SO-Airy beam used in Equation (2) are provided in the table. The phase mask, intensity distribution in the focal plane and their comparison to the equivalent normal structured beams is presented in Figure 2. Since the effective NA in our case is NAeff =0.55<0.7 the effect of input polarization of the beam on the focal plane intensity profile can be neglected32 and so we used the scalar diffraction theory33 to simulate the intensity profile in the focal plane. The Hermite–Gauss beam can also be realized by multiplying the exponential phase function with the Hermite polynomial, as done in Figure 2d1. Clearly, sub-diffraction features can be obtained for the structured SO beams as well as for the non-structured SO beam, as will be demonstrated in the next section.

Figure 1
figure 1

Super-oscillating (SO) beams generation. (a) A schematic of the optical setup; optical wave-fronts are modulated by the phase mask and focused through a microscopic objective lens to generate SO beams. (b–e) Three-dimensional (3D) volumetric profiles of the generated SO-structured beams—SO-Gaussian beam (SO-GB), SO-vortex beam with l=1, SO-Hermite–Gauss (SO-HG10) beam, and SO-Airy beam, respectively. Beams were created with relatively large features to better image their structure. The threshold intensity levels for the contour plots in b–e are 0.43, 0.34, 0.36 and 0.31 of the maximum intensity, respectively.

Full size image
Figure 2
figure 2

Gallery of generated SO beams: Gaussian beam, vortex beam of charge l=1 and l=3, HG10 beam and Airy beam. All the SO phase masks, their corresponding simulation and their experimental realizations are given in the first, second and third columns, respectively, while the experimental realizations of their counterpart normal beams are given in the last column. One-dimensional intensity plots of SO beams and their equivalent normal beams used to measure the FWHM are given in the fourth column in red and blue colors, respectively. Each beam profile is normalized to its own maximum.

Full size image

Results and discussion

We start by realizing a sub-diffraction-limited laser spot based on a Gaussian SO beam. The theoretical beam waist of the focal spot for a Gaussian beam illuminating the entire lens aperture is calculated by d=1.27λ/2NA and its FWHM is , but since in our set up we are using a Gaussian beam whose width is smaller than the lens aperture, the effective numerical aperture is NAeff=0.55. The measured FWHM=(427±58) nm agrees well with theoretical expectation of 0.38λ/NAeff=368 nm (Figure 2a5). With the same illumination, the measured FWHM of the central lobe = of a SO-Gaussian beam (generated with ) is a factor of ~2.6 smaller (Figure 2a3). Next, we show the ability of this method to generate sub-diffraction ‘doughnut’-shaped SO-vortex beams by substituting φobj=lθ in Equation (2). Owing to the helical phase term, the central lobe of this beam carries orbital angular momentum with topological charge l=1. The measured dark core size with rπ=0.70rmax is , more than a factor of 1.3 smaller than the achieved core with a diffraction-limited beam (compare Figure 2b3 and 2b5). We also generated SO-vortex beam with a larger topological charge l=3. For rπ=0.72rmax the dark core size is (790±58) nm, significantly smaller than the (947±58) nm dark core size of the corresponding diffraction-limited beam. Next, we generated self-similar super-oscillating HG10 beams, having two lobes with identical size for rπ=0.72rmax, where each lobe is significantly smaller than the diffraction-limited spot size, see Figure 2d3 and 2d5. The beam waist of SO-HG function is 1 mm in the phase mask, displayed on the SLM. Finally, we generated the SO Airy-like beam where for rπ=0.30rmax, the FWHM of the small lobe that is located to the right of the main lobe of the beam is . Its size is approximately only a quarter of the size of the main lobe of a normal Airy beam as shown in Figure 2e. Similar narrowing of the Airy lobe were observed recently under an appropriate transverse compression of their spatial spectra34, 35 and by superposition of Airy modes36.

Having established the superior focusing of SO beams, we are interested in their application to improving optical trapping. First, we demonstrate that optical trapping is possible with structured SO beams such as a SO-Gaussian beam, a SO-vortex and SO-HG beams, as shown in Figure 3 (Supplementary Movie 1). For this application, we used slightly larger lobes, although they are still beyond the standard diffraction limit. If we use the same beam profiles as given in Figure 2, the central and first side lobes are too close to trap 500 nm size particle at the central lobe of the SO beams and therefore the particle jumps from the central lobe to the side lobes. Hence, we chose to use slightly larger lobes where there is a sufficient gap between the central and side lobes, thereby enabling stable trapping of particles at the central lobe. The optical trapping force of dielectric particles is proportional to the gradient of the trapping laser intensity37. The localization quality is a function of both the focal spot size and the trapping force. It is therefore not straightforward to assume that a sub-diffraction-limited spot would result in stronger trapping or better localization. To characterize the properties of SO-Gaussian beams as optical traps, we compare the trapping of a single 500 nm polystyrene bead by either a diffraction-limited Gaussian beam (width ) or a SO-Gaussian beam (width ). Suspension of polystyrene beads, 500 nm in diameter (Invitrogen lots #1173396, Waltham, MA, USA), were placed between glass slide (1.1 mm in thickness) and cover slip (0.15 mm in thickness) to form a ~20 μm thick sample. We use dilute suspensions to control the number of trapped particles, and laser intensity to control the strength of trapping. In this way, we manipulated the particles to sit either in the central spot of a SO-Gaussian beam or the ring surrounding it against the slide. We use conventional video microscopy38 to extract the trapped particles’ trajectories from which we derive the 2D probability distribution of their position (Figure 3b and 3c), and the corresponding trapping stiffness39. The trapping results presented below correspond to lateral (2D) trapping balancing radiation pressure against a glass wall. Although the maximal intensity of the central lobe of the SO-Gaussian beam is seven times lower than that of the Gaussian beam, it is clear from Figure 3b and Figure 3c, that the SO-Gaussian beam confines the particle significantly better (Supplementary Movie 1). We performed single polystyrene bead trapping experiments for 11 different beads and observed the average s.d. of positions indicates nearly three-fold improvement in localization, for the SO-Gaussian beam versus for the Gaussian beam. We plot the histogram of the stiffness ratio between SO and normal Gaussian beam corresponding to the different trapping measurement of single polystyrene bead. The average localization improvement translates to a 9.4-fold improvement (see Supplementary Materials for details and Supplementary Fig. S8) in the trapping stiffness from to . Laser power arriving at the optical trap was 1 and 0.025 mW for Gaussian and SO-Gaussian beams traps, respectively. In terms of trapping efficiency (stiffness mW−1), the central lobe of the SO beam shows more efficient trapping by the factor of 350 times than the normal Gaussian beam. This huge enhancement in the trapping efficiency of SO beam is the result of the big difference between the power of central SO beam and normal beam. The relatively large variation in the trapping stiffness of the SO beam is due to its high sensitivity both to the axial distance from the focal plane and the alignment of the system (for more details see Supplementary Materials). We note that 200 nm polystyrene beads were also trapped using the SO-beam (see Supplementary Fig. S6a in Supplementary Materials), but we did not use them for analyzing the trapping stiffness, owing to their smaller size and resulting difficulty in precisely quantifying their movement.

Figure 3
figure 3

Particle manipulation with structured SO beams. (a) Trapping of single polystyrene bead of size 500 nm in diameter with the SO-Gaussian beam (SO-GB). (b, c) corresponds to 2D probability distribution of position of a single trapped bead of the normal Gaussian beam (GB) and SO-Gaussian beam, respectively. (d–f) Multiple particle manipulations with the SO-vortex l=1, SO-HG10 and SO-HG11 beams, respectively. (g–i) A time series showing the anticlockwise rotation of beads trapped in a SO-vortex beam of charge l=1, due to the transfer of orbital angular momentum from the SO-vortex beam to the trapped beads.

Full size image

Next, we studied particle manipulation with structured SO beams. Specifically, we demonstrated the ability of SO-vortex beam to transfer its OAM to polystyrene beads, enabling to simultaneously trap and rotate them at the vicinity of the dark core of size , see Figure 3g–3i. In addition, clockwise and counter-clockwise particle rotation is achieved by changing the sign of the topological charge of the SO-vortex beam (Supplementary Movies 3 and 4). Moreover, when we trapped particles in both the inner and outer rings we could distinguish between their rotations and infer the direction of the inner ring rotation. Also, we observed that in the SO-vortex beam profile both the inner and outer rings have the same sign of topological charge. Trapping multiple particles in sub-diffraction-limited traps can be done using SO-HG beams. In Figure 3e and 3f, we show two (four) particles, each one trapped in each one of the two (four) lobes of the SO-HG10 (SO-HG11) beam, each one having a lobe size . Higher order SO-HG beams are utilized for trapping of a single particle in each one of the beams’ lobes, enabling to control the number of trapped particles in a tractable manner by changing the beam shape in a sequence from HG22 to HG10, see Supplementary Movie 5. We observed that trapping occurs both in the ring and in the center at the same height as can be seen from the beam profile (Figure 1b) and from an image of trapped particles that appear at the same height (see Supplementary Fig. S6b in the Supplementary Materials). In other words, since we use high-index spheres, the outer rings will attract our particles and therefore destabilize their trapping in the central trap rather than increase their trapping stiffness. At low laser powers, we indeed see particles jumping from the center trap to the outer rings of the SO-GB. The same phenomena occur for the SO-vortex and SO-HG beams. Therefore, it is observed that all the generated SO beams, despite their lower intensity, but due to their smaller sub-diffraction size, have the ability to trap and manipulate particles.

To better understand the mechanism of the marked trapping enhancement in SO beams, we repeat the experiments with an infrared laser of wavelength λ=1083 nm. By using a longer wavelength, we can tailor the width of the SO beam to approximate the size of the trapped particle (500 nm), that is, the measured FWHM of the central lobe of SO beam is for rπ=0.65rmax, which minimizes the effect of the outer lobes of the SO beam on the trapped particle. In these conditions, the FWHM of the normal beam is , which agrees well with the theoretical diffraction limit with NAeff=0.55. The larger dimensions of the SO beam also facilitate its intensity profile characterization. For equal input laser power, the peak intensity of central SO lobe is about 20 times less than that of the normal beam’s peak intensity. For comparison purposes we maintain equal peak intensity for both the normal and SO beam traps, throughout the trapping experiments by tuning the input laser power (Figure 4a). To ensure trapping is in the focal plane of the SO beam, we demonstrate simultaneous trapping both in the center and outer lobes of the SO beams (see Supplementary Fig. S7 in the Supplementary Materials).

Figure 4
figure 4

Trapping results with the infrared laser. (a) Normalized experimental (dots) and simulation (lines) 1D beam profile of the SO (red) and normal (blue) beams for equal peak intensity. (b) Computed gradient force of SO (red) and normal (blue) beams, where the vertical lines show the maximal gradient force of the central lobes of both the beams. (c) Experimental 1D probability distribution of the single particle trapped in the central lobes of SO (red) and normal (blue) beams.

Full size image

Further insight into the enhanced trapping of the SO beam is obtained modeling the interaction of the light beam with a single particle, by approximating the optical trapping force37 at the experimental conditions by, (Figure 4b), and implementing it in a Brownian dynamics simulation of particle trapping40, where α is the particle polarizability (see Supplementary Materials for full description and Supplementary Fig. S5). In Figure 4b, the gradient force calculated theoretically from the known SO and Gaussian fields are compared, the maximal trapping force in the SO beam is nearly 2.3 times greater than that of normal beam. The enhanced trapping force results in an enhancement of trap stiffness by a factor of 9.1 experimentally (Figure 4c, Supplementary Movie 6), from for the Gaussian beam to for the SO beam, and a factor of 4.1 in simulations (). We find that localization is enhanced in the SO beams compared to normal beams in all experiments and simulations. In terms of trapping efficiency, the SO beam shows more efficient trapping by the factor of 80 times than the normal Gaussian beam. The difference in the trapping efficiency between the infrared and green lasers is due to the different size of the central SO lobe and power. However, experimentally the effect is more pronounced with respect to the theoretical prediction, probably because we use a simplified one-dimensional model that ignores the size effects of the trapped particle. A more sophisticated model using Mie scattering theory to calculate the optical forces in the optical trapping41 would be required to explain more accurately the trapping enhancement.

Conclusions

In conclusion, we have presented here a systematic method for the generation of structured super-oscillatory beams focusing light beyond the standard diffraction limit. Further, we showed that these structured beams can confine nanometer polystyrene beads with unsurpassed precision and force. The localization accuracy is much higher than that achieved by diffraction-limited Gaussian beam. The enhancement of the gradient force and the improved localization are also supported by a simple theoretical model, although the full mechanism responsible for the localization enhancement merits more detailed theoretical analysis. The sub-diffraction spots of the structured beams may be applied for STED microscopy11 (where SO-vortex beam and SO-Gaussian beam can be used for depletion and detection of fluorescent dyes), as well as in lithography. Finally, the method of structuring SO functions shown here can be used in other fields, for example, nonlinear frequency conversion31, plasmonics42 as well as in the time domain for structuring light pulses for super-transmission43 and for time-dependent focusing44.