Introduction

Knowledge of the relatedness between individuals in a population is of central importance to many aspects of biology, including population genetics, conservation and sociobiology (that is, Charpentier et al., 2012; Mattila et al., 2012; Liu et al., 2013). Although the coefficient of relatedness between individuals can be calculated from a known pedigree, in the absence of this information, relatedness can be estimated using genetic marker data. A number of estimators have been developed for this purpose and can generally be classified into two categories: method-of-moment and maximum-likelihood estimators.

Method-of-moment estimators substitute sample moments for the unknown population moment to estimate various population parameters. These methods can generate an unbiased estimation of relatedness, including either r directly (that is, Queller and Goodnight, 1989; Li et al., 1993; Ritland, 1996), or both r and Δ (four-gene coefficient, the probability that both genes of one individual are identical by descent (IBD) to both genes of another individual) simultaneously (that is, Lynch and Ritland, 1999; Wang, 2002; Thomas, 2010). Here we define r as the probability that an allele sampled from one individual at a locus is IBD to one of the alleles from the other individual. Although this IBD definition of relatedness is incompatible with that of Wright (1921), which was based on the correlation between individual allele frequencies (see Supplementary Files for details), the two definitions are identical in the absence of double reduction, inbreeding and selfing. According to IBD, r should range from 0 to 1. However, method-of-moment estimators can produce relatedness values outside of this range. This potential problem can be resolved by truncating the estimators, although this produces bias (Milligan, 2003; Wang, 2011).

The second method, maximum likelihood, was developed by Milligan (2003) and Anderson and Weir (2007) for estimating pairwise relatedness. This was based on the earlier work of Thompson (1975). Maximum likelihood estimates the probability of observing a given pairwise allelic pattern φ (two-gene coefficient, the probability that a single allele in one individual is IBD to one in another individual), Δ and the allele frequencies. By searching parameter space for φ and Δ values that maximize the probability of the genotype pattern observed, maximum-likelihood values can be determined. Because maximization can be limited to the parameter space as defined by probabilities of IBD, invalid values for the parameters are avoided.

Both methods are limited to making estimations based on disomic inheritance. Although some coefficient of coancestry estimators developed for diploids can be extended to polyploids (that is, Loiselle et al., 1995; Ritland, 1996), as has been done in the software SPAGEDI V1.4 (Hardy and Vekemans, 2002), they fail to directly estimate polysomic inheritance. A significant proportion of plant species are autopolyploid, with 30–80% of angiosperms showing polyploidy (Burow et al., 2001) and most lineages showing evidence of paleoploidy (Otto, 2007). Although rare, polyploidy is also present in animals (for example, Salmonidae fish, African clawed frog: Xenopus laevis, Weather Loach: Misgurnus anguillicaudatus). There are two distinct mechanisms of genome duplication that result in polyploidy: allopolyploidy and autopolyploidy. In allopolyploidy, chromosomes originate from two species; in autopolyploidy, all chromosomes originate within a single species, often due to unreduced gametes. This paper focuses on autopolyploids.

Because of their importance to agriculture, there has been much scientific investigation of plant autopolyploids (López-Pujol et al., 2004; Luo et al., 2006). In addition, autopolyploids do not exhibit disomic inheritance, whereas allopolyploids do so because of minor differences between chromosomes originating from different species (Luo et al., 2006). Polyploids displaying disomic inheritance can thus be described using normal diploid models once alleles are assigned to the alternative duplicated loci (cf Ritland and Ganders, 1985). However, diploid models cannot be applied to polyploids that display polysomic inheritance, that is, autopolyploids. Thus, few models apply directly to autopolyploids (cf Murawski et al., 1994; Thompson and Ritland, 2006). Here we focus on polyploids displaying polysomic inheritance, and introduce a maximum-likelihood method for estimating coefficients of relatedness for co-dominant markers in panmictic populations.

Theory and modelling

Identity-by-descent and relationship estimation

Most estimators assume that: (i) populations are large (that is, in the limit of infinite) and panmictic; (ii) there is no inbreeding; and (iii) individuals have autosomal loci with Mendelian inheritance. In diploids, the relatedness coefficient (r) can be calculated from two ‘higher-order’ coefficients:

Δ is the probability that two individuals share two alleles that are IBD at any given locus, and φ is the probability that they both share one allele that is IBD (Lynch and Ritland, 1999). For example, the probability that parents and offspring share an allele that is IBD is 1, so φ=1 and Δ=0; the probability that full-sibs share one or two alleles that are IBD is either 0.5 or 0.25, so φ=0.5 and Δ=0.25. The φ and Δ for specific relationships are listed in Table 1.

Table 1 Relatedness coefficients for specific relationships in diploids and tetraploids in the absence of selfing, inbreeding or double reduction
Full size table

Using the same assumptions and assuming no inbreeding or double reduction, in tetraploids, the relatedness coefficient can be expressed as:

where , and Δi is the probability that two tetraploids share i alleles that are IBD at any given locus. For relationships between polyploids in outbred populations, r is equivalent to that of diploids. The values of deltas for tetraploid relatives, assuming no double reduction (in polyploids, the phenomenon in which two chromatids of a single chromosome can pass to a same gamete; Mather, 1936), are shown in Table 1.

For inbred populations, Jacquard (1972) described a set of nine identity-by-descent configurations that fully describe the possible IBD relationships between a set of four alleles possessed by two diploids. These are denoted d1,…,d9 and are shown in Figure 1. The probability that a pair of individuals are in IBD mode di is denoted as δi. Therefore, the coefficient of coancestry (denoted as θ, an equivalent parameter measuring the probability that two alleles, one randomly drawn from each individual, are IBD; Jacquard, 1972) is:

Figure 1
figure 1

Configurations of identity by descent between two diploids. In each subfigure, the two upper dots represent the two alleles of one individual, whereas the other two represent the alleles of the second individual. The lines indicate alleles that are IBD.

Full size image

Here, the coefficient of δi is the number of IBD allele dyads between two individuals of di (Figure 1). In outbred populations, the two alleles in a single individual cannot be IBD, so the first six IBD configurations are not possible and δi=0 (i=1,…,6), reducing Equation (3) to Equation (1), and r=2θ.

The possible IBD relationships between tetraploids are more complex, with a total of 109 IBD configurations possibly existing between two individuals (see Supplementary Materials). Because this estimate assumes outbreeding, we do not further consider inbreeding. Thus, only five configurations are possible, denoted Di (0⩽i⩽4, where i is the number of IBD alleles shared by two individuals). The IBD configuration for a pair of individuals cannot be obtained from their genotypes, because alleles with the same allelic type may not be IBD. However, alleles identical by state (IBS) can be determined; these are alleles sharing the same allelic type, which include those that are both IBD and non-IBD.

There are 9 and 109 IBS configurations in diploids and tetraploids, respectively. Denoted as s1,…,s9 and S0,…,S108, their patterns are similar to IBD configurations. For diploids, the lines in Figure 1 represent alleles with the same allelic type. IBS modes for autotetraploids are given in Supplementary Materials.

Under the assumption that two individuals belong to a single population that conforms to the Hardy–Weinberg equilibrium, the probabilities of observing each IBS configuration (S), conditioned on a particular IBD mode (D), can be calculated. The conditional probabilities of five outbred IBD configurations, in which one genotype is AiAiAiAi, are shown in Table 2. Additional conditional probabilities can be generated by an additional programme (see Supplementary Files). The conditional probability is the sum of the products of the probabilities of three sub-genotypes:

Table 2 Probability of specific identity-in-state patterns, given the mode of identity by descent if the genotype of one individual is AiAiAiAi
Full size table

Where Gab is the IBD sub-genotype shared by two individuals, and Ga and Gb are the additional two non-IBD sub-genotypes of two individuals a and b, respectively. The sub-genotype is a subset of a genotype if a genotype can be defined as a multiple set, because the sub-genotype of a tetraploid can consist of zero to four alleles. Pr(G) is the probability of choosing G from sub-genotypes with the same number of alleles as for G. For example, , where pi and pj denote the allele frequencies of Ai and Aj, respectively.

Taking Pr(AiAiAiAi, AiAiAiAj|D2) as an example, there is only one possible Gab, Ga and Gb: Gab=AiAi, Ga=AiAi and Gb=AiAj. Using the probabilities given in Table 2, the single-locus likelihood of a specific relationship with Δ=[Δ4,…,Δ0]T between two individuals can be calculated. When the IBS mode of those individuals is S, conditioning on the IBD mode yields:

Although each locus is characterized by its own set of allele frequencies for multilocus estimation, the degree of relatedness between the two individuals (Δ) is constant across loci because it represents their overall relatedness to each other. Therefore, the multilocus likelihood for unlinked loci is obtained by taking the product of the single-locus likelihoods. The logarithm of likelihoods (L*) for each loci is computed to simplify the calculations, and their summary is denoted as .

Parameter space

The maximum-likelihood estimate of Δ is found by searching the parameter space until a maximum is found. In outbred populations, the parameter space of Δ is ∑Δi=1 and 0⩽Δi⩽1. Another constraint for diploids in outbred populations was given by Thompson (1976): diploid IBD parameters Δ and φ are subject to the constraint 4Δ(1−Δ−φ)<φ2, which is applied by Anderson and Weir (2007) but not by Milligan (2003). We considered the situation in which two individuals have fathers who are related and mothers who are also related, but the mother and father of any given individual are unrelated. Under such conditions, p and q were the probabilities that two individuals shared an IBD allele inherited from their fathers and mothers, respectively. As these two events are independent, the diploid IBD parameters Δ and φ can be expressed as follows:

and

where 0⩽p and q⩽1. Following the same procedures, we assumed that pi is the probability that two tetraploids from an outbred population share i IBD alleles inherited from their fathers, and qi is the probability for i IBD alleles inherited from their mothers. Thus, the tetraploid IBD parameters Δi can be expressed as:

Thus, the constraint for Δ can be calculated although complicated to express, and equivalent information is contained within pi and qi. Therefore, we used pi and qi instead for searching as they are inside the parameter space, making the tetraploid IBD parameters valid. By simulation, we found that Thompson’s (1976) constraint can reduce bias of the likelihood estimator.

Genotype ambiguity

A distinct feature of polyploidy population genetics is the formation of partial heterozygotes. Alleles can vary in number from 0 to 4 copies in tetraploids. For example, there are three types of partial heterozygotes (that is, AiAiAiAj, AiAiAiAj and AiAjAjAj) if two alleles (Ai and Aj) are present in an ambiguous genotype. Although some methods are able to determine tetraploid genotype (that is, Xu et al., 2002; Pfeiffer et al., 2011; Serang et al., 2012; Voorrips et al., 2011; Uitdewilligen et al., 2013), additional instrument or software may be required.

We describe an alternative method to estimate the coefficient of relatedness in scenarios in which heterozygote genotypes are unclear but allele frequencies are known. If two types of alleles, Ai and Aj, are detected in an individual, the probability ratio of the three possible genotypes AiAiAiAj, AiAiAjAj and AiAjAjAj is . Similarly, if three alleles are detected, Ai, Aj and Ak, the probability ratio of the three genotypes AiAiAjAk, AiAjAjAk and AiAjAkAk is . Subsequently, each possible genotype dyad of the two individuals is weighted by its probability, allowing Equation (6) to be modified to:

where Pj,k is the probability of kth possible genotype pairs at the jth locus, and is the logarithm of this value. The remaining steps are unchanged, and after the most probable is found, is obtained by Equation (2). In general, an algebraic solution is impossible (Milligan, 2003). As a result, a downhill simplex algorithm is used to search for the that maximizes the likelihood within the parameter space. The simplex consists of ν+1 points (each representing a Δ). If the distance between the points with the minimum and maximum likelihoods is below 0.00001, the algorithm is convergent and the iteration is terminated. A new simplex is then generated by adding a value of the current best point in each dimension, and repeating to prevent the simplex from being trapped in a ridge. An error <0.0001 for tetraploids can be achieved with ~600 attempts. Using these methods, this model can be applied to any level of ploidy by replacing the four with v (the level of ploidy) in Equation (2). The conditional probabilities in Table 2 from haploid to octoploid can be generated (see Supplementary Files). However, for species with an odd number of ploidy, Thompson’s (1976) constraint cannot be applied.

Polyploid method-of-moment estimator

Huang et al. (2014) developed a method-of-moment estimator for polyploids, which models the probability of each similarity index conditioned on the reference genotype (see also Lynch and Ritland, 1999). The similarity index is defined by the number of alleles that are identical in state between two individuals. However, for this method, unlike for diploid estimators (that is, Wang, 2002; Ritland, 1996), each allele is counted only once. For example, in autotetraploids, the similarity index for each locus has only five values (0, 0.25, 0.5, 0.75 and 1). Table 3 summarizes similarity indices and probabilities of proband genotypes given the allele frequencies and the array of deltas for reference individual AiAiAiAi. By summarizing the expressions with the same similarity index for a reference genotype pattern (Table 3), the following equation is established:

Table 3 The similarity index and coefficients of probability for reference individuals AiAiAiAi
Full size table

where Δ is a column matrix consisting of all ‘higher-order’ coefficients from Δ4 to Δ1. Each element in P is the probability of the corresponding similarity index being observed, and E is the probability that a certain similarity index is observed when relatedness is 0 (the column with the header of 1 in Table 3). M is the matrix consisting of four columns headed by deltas in Table 3. The moment vector of the similarity index consisting of the first to fourth moments can be expressed as:

Where C is a 4 × 5 matrix with Cij=[1−0.25(j−1)]i. Equating the observed moments to the expected (S=Ŝ) and estimated deltas to the true deltas solves the estimator as:

The single-locus r̂ can be obtained from Equation (2), whereas in multilocus estimation the locus-specific weight is given by the inverse of the variance of r̂. This is calculated numerically by Var(X)=E(X2)−E2(X). The estimate across all loci is the weighted average of each estimate of each locus, with both individuals being used for reference; the final r̂ is the arithmetic mean of the two estimates. Huang et al. (2014) also developed a solution to address ambiguous genotypes using this estimator: the matrices E and M are weighted by the probability of each reference genotype, and P is weighted by the probability of each proband–reference genotype pair.

Coefficient of coancestry estimators

Some coefficient of coancestry estimators (θ) developed for diploids can be extended to polyploids (for example, Loiselle et al., 1995; Ritland, 1996). Although θ is alternatively defined as the correlation between the additive values of the two individuals (Ritland, 1996), here we continue with the IBD definition used by other estimators: θ is the probability that a pair of alleles randomly sampled from two individuals at a locus are IBD. In diploid outbred populations, θ=1/4 for parent–offspring, θ=1/4 for full-sibs, θ=1/8 for half-sibs and θ=1/16 for first-cousins (Jacquard, 1972). The first estimator presented by Ritland (1996) is used as an example and compared with our maximum-likelihood estimator.

Ritland’s (1996) estimator assigns a similarity index (Si) to a genotypic pair for each of n possible alleles. For a diploid, there are four possible values of the ith allele: 0 (one or no individuals contain Ai), 1/4 (both individuals contain a single Ai), 1/2 (one individual contains two and the other individual one Ai) or 1 (both individuals are homozygous for Ai). The single-locus estimator of Ritland (1996) is given by:

Hardy and Vekemans (2002) expanded these estimators to higher levels of polyploidy by expanding the definition of the similarity index Si to a product of the frequency of Ai in the two individuals:

Relatedness can be obtained by Equation (12). However, by doing so the estimator becomes biased. To obtain an unbiased estimator, we use the harmonic mean of and as the denominator, therefore the single-locus relatedness estimator is:

In multilocus estimation, the final estimated relatedness is the weighted average of r̂ for each locus, and weight is the inverse of the expected summation of the similarity index across alleles for outbred non-relatives, which is also the allelic richness of this locus.

Using Equation (8), the relatedness coefficient can also be estimated using the method of Loiselle et al. (1995). When the allele frequency within an individual is equal to the population allele frequency (for example, a heterozygote at an uniform biallelic locus), will be 0. To avoid obtaining an undefined final estimated relatedness, the r̂ at such loci is not taken into account for calculating the weighted average of r̂.

These coefficients of coancestry estimators consider situations in which inbreeding occurs, but do not incorporate ‘higher-order’ coefficients used in this paper’s estimator. To handle ambiguous genotypes, the similarity indices are weighted by the probability of each possible genotype pair.

Calculating relatedness from pedigrees

The coefficient of coancestry can be calculated from pedigree data by a recursive algorithm (Karigl, 1981). For polyploids, the coefficient of coancestry between two individuals is the same as in diploids:

Here, a, b, f and m are individuals, and f and m are the father and mother of a, respectively, where the probability that an allele in f or m is inherited by a is 1/2. It can be inferred that a cannot be an ancestor of b because Equation (9) becomes divergent. If b is an ancestor of a, then another algorithm is needed to calculate the coefficient of coancestry of an individual with itself. This can be achieved using the equation:

where ν is the level of ploidy. Clearly, θab=θba and θab=0 if a and b are not related, such that the coefficient of coancestry can be calculated by iteration or recursion for any situation once the ancestry of a and b is known.

In polyploids, multivalent formation can result in double reduction, which occurs when sister chromatids segregate into the same chromosome (Darlington, 1929). Under pure random segregation, the rate of double reduction, α (Fisher and Mather, 1943), assumes a minimum value of 0, and increases to 1/7 (with pure random chromatid segregation) and 1/6 (with complete equational segregation) for tetrasomic inheritance (Muller, 1914).

If double reduction is considered, the Equation (10) to calculate the coefficient of coancestry within the same individual should be modified. For octosomic or decasomic inheritance, there are three rather than two types of origins for the gamete, so an additional parameter is needed for the segregation ratios (Fisher and Mather, 1943). Here, αi is the probability that double reduction occurred i time(s) in a gamete (∑αi=1, 0⩽i⩽[v/4]), and θaa is given by:

The derivation of Equations (10) and (11) can be found in Supplementary Files. Equation (11) can be inferred from the coefficient of coancestry within the same individual from an outbred population at equilibrium (the genotypic frequencies are equal among generations). This is written as:

Where θaa=0.3 for tetraploids under purely random chromatid segregation. In the presence of double reduction, Equation (9) remains unchanged. In tetraploids, for example, although the probability an allele in f or m is inherited by a is 1/4 under double reduction, the number of IBD allele pairs between a and b is also doubled.

In the absence of double reduction, inbreeding or selfing, the relatedness coefficient can be calculated from r=4θ. However, it cannot be applied because r may exceed 1. By Equations (5) and (6) presented by Hardy and Vekemans (1999), Wright’s coefficient of relationship can be calculated from the coefficient of coancestry as:

Which is used as the true relatedness for simulation; the derivation of Equation (12) is given in Supplementary Files.

Statistical behaviour of estimators of relatedness

To investigate the statistical behaviour of estimators, six estimators were compared. These included the maximum-likelihood estimator (ML) described in this paper, the method of moment for polyploids (MOM; Huang et al., 2014) and a coefficient of coancestry estimator (RI; Ritland, 1996), applied when genotypes are known and when genotypes are ambiguous, the latter of which are denoted ML*, MOM* and RI*. All estimators were truncated to the range of 0–1 for ease of comparison.

Four comparisons considering various conditions were performed: (i) the distributions of r̂ in a particular relationship; (ii) the performance of multilocus estimations in ideal conditions; (iii) the minimal number of loci needed to achieve specific requirements; and (iv) the robustness of these estimators in a finite population with strong genetic drift, inbreeding and double reduction.

Distribution

For this application, four relationships (parent–offspring, full-sibs, half-sibs and unrelated) were simulated. For each pair of individuals, the genotype of one individual was randomly generated according to the Hardy–Weinberg equilibrium. The other genotype was then obtained from the randomly generated genotype as a reference and their relationship . A triangular allele frequency distribution was simulated, where this followed the proportions 1, 2,…,n. Numerical results were obtained from Monte Carlo simulations assuming true allele frequencies were available. The results are given in Figure 2 using five loci, each segregating for eight alleles because eight was the minimum number needed to display all 109 IBS configurations. Their distribution under other settings can be found in Supplementary Materials.

Figure 2
figure 2

Distribution of r̂ estimates between autotetraploids using six different methods (ML, MOM and RI for exact genotypes, ML*, MOM* and RI* for ambiguous genotypes) for four relationships (PO for parent–offspring, FS for full-sibs, HS for half-sibs and UN for unrelated). Each distribution was based on a sample of 200 000 estimates taken from five loci, each segregating for eight alleles with their frequencies drawn from the triangular distribution.

Full size image

Figure 2 shows that the likelihood estimators exhibited less variance for kin dyads. However, for non-relatives, the RI and MOM estimators gave a higher frequency of 0 estimates. Furthermore, the ML* estimator converged near the true value even when the correct genotype was unavailable. In contrast, the MOM* and RI* estimators both showed negative bias in relatives.

Root mean square error

This application used multiple multiallelic loci to estimate relatedness for specific relationships under ideal conditions: population size was sufficiently large, true allele frequency was available, mating was random, inbreeding was absent and chromosome segregation was purely random.

Because both truncated and maximum-likelihood estimators have a bias, the root mean square error (RMSE), which incorporates bias and sampling variance, was used to measure overall accuracy. RMSE can be calculated by the following equation: .

In this section, the number of loci (l) was simulated from 1 to 100, with each locus segregating five or ten alleles with their frequencies drawn from triangular distribution. The results for each relationship type were calculated for 15 000–100 000 pairs of individuals. The number of dyads simulated was dependent on l; with smaller values of l, more simulations were performed to smoothen the curves. The RMSE of r̂ is shown in Figure 3.

Figure 3
figure 3

Multilocus RMSE of r̂ between autotetraploids as a function of the number of alleles under a triangular allele frequency distribution. Six estimators were compared, including the polyploid maximum-likelihood estimator (ML, first row), the truncated polyploid method-of-moment estimator (MOM, second row), the truncated Ritland (1996) estimator (RI, third row) and their respective modified versions that support ambiguous genotypes (denoted by an asterisk after the estimator abbreviation). Two kinds of loci were simulated: (1) penta-allelic (n=5, two leftmost columns) and (2) deca-allelic loci (n=10, two rightmost columns). Results were obtained by generating 15 000–100 000 pairs of four relationships including parent–offspring (‘—’), full-sibs (‘– –’), half-sibs (‘– .’) and unrelated (‘…’) using Monte Carlo simulations.

Full size image

Figure 3 shows that different estimators behaved differently statistically. The ML estimator yielded the largest RMSE for non-relatives and half-sibs. Although the RI estimator exhibited a large RMSE for related dyads, the RMSE of these relationships was relatively small for the MOM and ML estimators.

If the correct heterozygous genotypes were unavailable, all the performance of all estimators was reduced. However, when the number of alleles was high, the performance of both the ML* and MOM* estimators improved. For both the RI and RI* estimators, an increase in alleles made little difference to estimator performance.

Confidence intervals

We also evaluated the requirements to distinguish particular relationships. We calculated the minimal number of loci needed to obtain a 95% confidence interval of±0.05 units of r (the probability that is 0.95), with ploidy levels ranging from diploid to octoploid. Bias was high when ambiguous genotypes were used for the estimations, and r̂ did not converge to the true value (Figure 2). As a result, we did not consider ambiguous genotypes for this application. Moreover, because the RMSE of half-sibs was usually the highest among the relationships tested (Figure 3), we only calculated half-sibs for simplicity. Results are shown in Figure 4.

Figure 4
figure 4

The minimal number of loci required to obtain a 95% confidence interval±0.05 units of r in half-sibs showed in Figure 3. Three estimators were compared in diploids (‘—’), tetraploids (‘– –’), hexaploids (‘– .’) and octoploids (‘…’). Results were obtained by the split-half method and 30 000 Monte Carlo simulations per attempt.

Full size image

The ML estimator required fewest loci to achieve a high degree of accuracy, nearly 90 and 85% of what was required for the MOM and RI estimators, respectively. Because polyploids have more copies of alleles and genetic information than diploids, the minimal number of loci required for higher levels of ploidy was fewer than that for multiallelic loci. By contrast, in biallelic loci or loci with few alleles, the probability that two non-relatives share IBS alleles was higher for polyploids. Therefore, at higher levels of ploidy, more loci were needed if the loci possessed few alleles, especially for biallelic loci.

Finite populations

Although these estimators performed reasonably well under the given assumptions, real cases often diverge from ideal conditions. To simulate nature, we simulated a finite population with strong genetic drift, inbreeding and selfing. Following Toro et al. (2011), the generations originated from 20 founder individuals. The genotypes of the founder individuals were randomly generated according to the Hardy–Weinberg equilibrium.

Ten discrete generations each consisting of 20 individuals were simulated. The parents of an individual were randomly selected from the last generation (some individuals did not reproduce) resulting in a data set of 200 individuals and 20 100 dyads. The true relatedness coefficients were computed from the pedigree using Equation (12), and the estimate of relatedness was obtained using the six estimators (Figure 3). To compute the estimators, we used the observed allele frequencies calculated from the genotypes of the 200 individuals. Because we do not develop a method for estimating allele frequencies from ambiguous genotypes in this paper, the observed allele frequencies were obtained from the true genotypes.

Four kinds of loci were simulated, including two with too few alleles to generate the 109 IBS modes (2 and 5 alleles) and two with enough alleles (10 and 15 alleles). For each simulation, 20 unlinked loci were used with their initial allele frequencies drawn from a triangular distribution. The mean true relatedness (r̂) of the simulated populations varied between runs due to random mating. In particular, inbreeding in the first few generations may lead to an increase in (r̂). Therefore, for each locus type, the simulation was repeated 40 times to ensure that (r̂) for different numbers of alleles was the same. Monomorphic loci were not used because the estimators failed to give a valid estimate. A linear equation r̂=β1r+β0 was used for regression analysis, the weighted least-squares solution was obtained and the coefficient of determination (R2) and RMSE calculated (Table 4; Figure 5). Additional results from varying numbers of loci and alleles are presented in Supplementary Materials.

Table 4 Statistics of r̂ for a finite population of autotetraploids
Full size table
Figure 5
figure 5

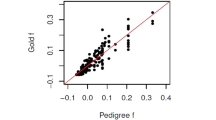
Marker-based estimated relatedness (r̂) as a function of pedigree-based true relatedness (r) in a finite population. Twenty unlinked loci were used in the estimation, each initially segregating with 10 alleles under triangular distribution. Each figure shows 4000 points randomly selected from 402 000 dyads. The top two rows show results for a population without double reduction, the bottom two rows show a population with double reduction. The second and fourth rows include genotype ambiguity. The trend lines for truncated (‘—’) and original (‘– –’) estimators were obtained by weighted least-squares regression.

Full size image

We also investigated the effect of double reduction on these estimators. The double reduction rate was assumed to be 1/7 in these simulations (Muller, 1914). To obtain a distribution of genotypes in equilibrium, each individual in the founder population was produced from eight temporary generations of non-relatives, in which individuals in the first temporary generation had a θaa=0.25. The true relatedness coefficient was obtained using Equations (9) and (11). Therefore, in the founder population, the coefficient of coancestry for the same individual was 0.299998≈0.3, whereas that between different individuals was 0. The other parameters were the same as in the previous application, and results are shown in Table 4 with α=1/7 in the first column (Figure 5).

The MOM* estimator encountered the singular matrix problem at n=5, and the RI estimator performed worse for biallelic loci, whereas the ML estimator was more stable (Table 4). Although the R2 of the RI estimator increased as n increased, the RMSE did not change significantly, unlike in the other two estimators. Due to small population size and strong drift, some alleles were lost in the last few generations, reducing the performance of the estimators compared with results shown in Figure 3, even for a higher initial number of alleles (n=15). Moreover, the range of estimates for all estimators was restricted to (0, 1), so the slopes deviated from 1.

Double reduction did not thus affect the distribution of true relatedness. However, the performance of all estimators was slightly reduced.

In Figure 5, most values of r lie in the range (0, 0.5). The points of parent–offspring pairs formed a vertical line at r=0.5 in the MOM and RI estimators. Because these estimators cannot give an accurate estimate for r, the longer length of these lines at r=0.5 suggests a larger RMSE. In contrast, a similar line was absent in the ML estimator because the variance of the estimates was too small, resulting in overlapping points. However, for half-sibs and grandparent–offspring pairs (r=0.25), other types of outbred relationships (r=0.125 or 0.0625) or ambiguous genotypes, sampling variance increased, so vertical lines are present. The line of the ML estimator was usually the shortest, suggesting a lower RMSE.

Similar to estimates of 0 or 1, there are two estimates (Δ2=1 or Δ1=1) that also lie on the edge of parameter space. If two individuals share only one or two IBS alleles at all loci, these parameters produce the largest likelihood and give an estimate of r̂=0.5 or 0.25, respectively. As a result, there were two additional horizontal lines in the ML estimators.

The results for the original estimators (without truncation) can be found in Supplementary Materials. Truncation can be expected to cause a reduction in slope and RMSE and an increase in R2. Nonetheless, the ML estimator still had better statistical values, with the exception of the slope, as the slope of the original MOM estimator was closer to 1.

Discussion

Statistical behaviour

We developed a maximum-likelihood method for estimating the relatedness coefficient for polyploids. The probability of observing an IBS mode conditioned on each IBD mode was calculated by following existing procedures (Thompson, 1975). A numerical algorithm was subsequently applied to find the optimal solution for r̂, and the statistical behaviours of various estimators of relatedness for autotetraploids were simulated and compared. Marker-based relatedness estimates typically showed large sampling variance, due to variance in identity by descent among loci and in identity-by-state alleles that are not IBD (Lynch and Ritland, 1999). The RMSE and variance were reduced by increasing the number of loci or by switching to loci that were more polymorphic. Overall, likelihood estimators exhibited lower RMSE than other estimators we examined for relatives, whereas the ML estimator produced a higher RMSE for non-relatives (Figures 2 and 3). The RMSE of estimators decreased rapidly as a function of l in multilocus estimations (Figure 3).

The RMSE of the likelihood estimator for unrelated dyads was highest because the estimator also generated IBS configurations that shared some IBS alleles by chance. This resulted in a positive estimate of r (Figure 2). Because each locus had eight total alleles that could be sampled between individuals, the probability that unrelated tetraploid dyads shared IBS alleles was higher than that for diploids, especially for biallelic loci. As a result, all estimators performed worse for biallelic loci (Figure 3; Table 4). For this reason, for hexaploids and octoploids, more alleles were required.

The MOM estimator may encounter a singular matrix problem when the number of alleles is too small (Huang et al., 2014). Singularity or near singularity can result from zero or near-zero coefficients in the set of equations, making Equation (7) unsolvable. This problem can also occur for diploid estimators. For example, for biallelic loci with uniformly distributed allele frequency, the Lynch and Ritland (1999) estimator has a sampling variance of infinity. Unfortunately, this scenario is more frequent for polyploids, but the probability of a singular matrix is reduced when the number of alleles is greater or equal to the level of ploidy (Huang et al., 2014). However, this does not guarantee that singularity is avoided, because some combinations of allele frequencies can also result in a singular matrix.

Ambiguous genotypes

When genotyping polyploid heterozygotes, balanced heterozygotes cannot be distinguished from unbalanced heterozygotes. In this case, each candidate genotype pair is weighted by its probability. This situation also brings a negative bias to both the likelihood and moment estimators. The true genotype pair of a kin dyad is diluted by other candidate genotype pairs that are usually less similar. For example, in a pair of tetraploid clonemates, both genotypes are AiAiAiAj. Therefore, each has three possible genotypes (AiAiAiAj, AiAiAjAj and AiAjAjAj) and there are nine combinations of genotype pairs. Three pairs give accurate estimates. Estimates of the other six pairs are <1, and the final r̂ is a maximum-likelihood solution (ML) or a weighted average (MOM or RI). Under such conditions, all estimators are less efficient, but in particular, the RI estimators are unusable if the number of alleles is too few. The ML estimator performs better than other estimators under most conditions (Table 4).

Inbreeding, selfing and double reduction

The new likelihood estimator assumes no inbreeding or double reduction, so that the number of non-zero ‘higher-order’ coefficients is equal to the level of ploidy and the range of r̂ is (0, 1). Because the probabilities of inbreeding, selfing or double reduction IBD configurations are not modelled, some estimates may be inaccurate. For example, the genotype patterns AiAjAkAl and AiAiAiAi do not have a higher estimate than AiAjAkAl and AiAmAnAo. If inbreeding, selfing or double reduction occurs, the former genotypes are more similar and should be assigned a larger r̂. Therefore, underestimation occurs for the likelihood estimator (that is, the slope deviates from 1 in Table 4).

There are nine IBD configurations for diploids. By contrast, IBD/IBS models for autotetraploids are more complex, with a total of 109 distinct configurations. The number of IBD configurations increases from haploid to octoploid, with 2, 9, 31, 109, 339, 1043, 2998 and 8405 possibilities, respectively. Because there are too many deltas in polyploids, it is impossible to solve for each delta. As a result, IBD configurations that involve double reduction and inbreeding were omitted from this model. However, a finite population including both inbreeding and double reduction was simulated, and regression analyses were performed to evaluate the statistics. Although all estimators were less efficient than under ideal conditions (a larger RMSE and greater sensitivity to the initial number of alleles because of the strong role of drift), the likelihood estimator showed greater robustness in simulation and was superior to the other estimators for multiallelic loci regardless of double reduction (Table 4; Figure 5). The MOM estimator performed well when there were multiallelic loci, and the original MOM estimator (without truncation) had the largest slope (>0.8; see Supplementary Material).

Biallelic markers

The likelihood estimator can be applied to a wide range of data, including microsatellites, single nucleotide polymorphisms and other co-dominant markers. However, because fewer alleles reduce accuracy, we suggest that only loci with many alleles be used, particularly if an application requires a high level of accuracy. Loci containing few alleles (for example, biallelic loci) can only achieve high levels of reliability with many. However, the number of unlinked loci is limited in the genome and with many loci, there is increased risk that adjacent loci will be linked and thus not represent independent data points. Although linked loci do not introduce bias, they do not increase reliability. This causes the RMSE to reach an asymptote as the number of loci increases. Furthermore, where genotypes are ambiguous, biallelic loci are also problematic as the bias is too large (Figure 5). However, single nucleotide polymorphism data can still be used, especially with newer genotyping-by-sequencing and haplotype prediction technologies (Xu et al., 2002; Uitdewilligen et al., 2013). These techniques provide means for unambiguous genotyping and also determine the haplotype. The haplotype of adjacent single nucleotide polymorphisms can be treated as an allele of a multiallelic locus, which can largely improve the reliability of estimation.

Properties of polyploids

Alleles in polyploids have more copies, so contain more information than alleles in diploids (Huang et al., 2014). Therefore, for multiallelic loci, fewer loci are required to achieve the same reliability for polyploids (Figure 4). Nevertheless, it is noteworthy that the chance of two non-relatives or less-related individuals sharing IBS alleles is higher under the same conditions, which can interfere with estimation and result in a positive bias. For example, more loci are required for higher levels of ploidy when alleles are few (Figure 4).

In extreme allotetraploids, there are two homologous sets each consisting of two homologous chromosomes. If a chromosome exclusively pairs with its homologue, this leads to disomic inheritance (Stift et al., 2008). For these cases, we can use diploid estimators. Some empirical studies show that many polyploids are actually in the intermediate inheritance (Allendorf and Danzmann, 1997; Jannoo et al., 2004). Intermediate inheritance may be expected in fertile interspecific hybrids, as their parents are usually related and therefore are expected to possess some degree of chromosomal homology (Jannoo et al., 2004), leading to complex mixtures of disomic and polysomic inheritance. Gametic and genotypic frequencies also deviate from expectation, resulting in additional positive bias for the ML and MOM estimators (see Supplementary Material), whereas the RI estimator is not affected.

Conclusions

Overall, the maximum-likelihood estimator we developed provides several advantages over existing methods. First, it generally exhibits lower RMSE compared with other estimators. Second, all estimates fall within a biologically meaningful range, and ‘higher-order’ coefficients can be explained as probabilities. Thus, the biological interpretation of individual estimates is straightforward. Third, it provides a solution for situations in which the allele dosage cannot be determined.

Although the maximum-likelihood estimator of relatedness performed well in simulations, there are conditions under which other estimators performed better, according to specific metrics. There is no single estimator with superior performance under all conditions and by all metrics. For specific applications under specific research conditions, it is possible to identify one optimal estimator. The software package POLYRELATEDNESS provides a simulation function that helps researchers evaluate the performance of each estimator under their given conditions.

Data archiving

The software POLYRELATEDNESS V1.4 (Huang K, Northwest University, Xi'an, China), user manual and example data set are available on Google Project (http://polyrelatedness.googlecode.com).