Introduction

Transformation optics1 (TO) provided a new way to design sophisticated electromagnetic devices using the form invariance of Maxwell's equations under coordinate transformations1,2. To implement the intricate gradient permittivity and/or permeability distributions designed by the TO theory, many researchers employed the novel concept of artificially structured metamaterials, which consist of deeply subwavelength unit cells coupling with electromagnetic waves collectively as an effective medium. From the first introduction of TO theory1, various TO applications have been suggested using metamaterials, such as cloaking1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17, arbitrary light guiding18,19, extreme imaging lenses20,21,22,23 and other interesting approaches to manipulating light24,25. Amongst those applications, invisibility cloaks1,2 contributed most significantly to the continued public curiosity and led to the expansion of related research fields26,27. The omnidirectional TO cloak1 effectively compresses an object to appear as a singular point, making it invisible from all directions; however it requires a wide range of refractive index between zero and unity, which is very difficult to achieve in realistic media without significant loss or dispersion3,4,5. This grand challenge has been tackled by only a handful of experimental efforts in the microwave6,7 and optical8 frequency domains. On the other hand, the carpet cloak device compresses an object to a flat sheet, which requires only modest ranges of material properties9. Moreover, for the TE polarization (out of plane E-field), a carpet cloak transformation can be implemented entirely without magnetic properties; consequently, they have been designed with large operational bandwidth and negligible attenuation10,11,12,13,14,15,16,17. The absence of magnetic response in carpet cloak is best understood using the conformal2 and quasi-conformal9 TO theory; it turns out to be closely related to the local isotropy of the underlying coordinate transformation28. Since exact conformal maps are very restrictive, the majority of devices based on locally isotropic metamaterials resort to quasi-conformal maps (QCM)9. QCM-based TO has already enabled numerous electromagnetic devices made of dielectric materials only, such as carpet cloaks10,11,12,13,14,15,16,17, arbitrary-shape waveguides18,19, or lenses20, all of which can operate with low loss and broad bandwidth.

If a quasi-conformal transformation optics (QCTO)-based device has a deviation of its boundary shape, for example, resulting from an elastic deformation, the device requires a complete redesign in order to preserve its functionality. To prevent degraded performance and maintain original function under an external load or other elastic deformation, self-adjustable metamaterials are necessary. Recently, a concept of smart metamaterials was introduced, which was conceived to enable shape reconfigurability of QCTO-based devices28. It was suggested that, in two dimensions - that is, for devices having long extruded shapes and limited to in-plane wave propagation – so-called hyperauxetic (having Poisson ratio less than −1) materials would be necessary for an exact implementation of this idea. Here, we present a rigorous derivation of Smart Transformation Optics (STO) in two dimensions and clarify the effect of choosing a plane stress vs plane strain configuration on the mechanical properties of smart metamaterials.

In a smart TO device, the boundary mechanical load should deform each unit cell so that the new distribution of electromagnetic properties would implement the desired TO map; in our case, TO maps must be limited to conformal or quasi-conformal transformations. In general, it is very difficult to integrate TO and solid mechanics, because the stress and strain distributions of a loaded structure in mechanical deformation are solutions of complicated equations - the generalized Hooke's law, which is the governing equation of elastodynamics for linear elastic materials29. By noting the fact that the sum of angle changes (α + β, in Fig. 1a) between unit cell's four sides is represented as shear strain in solid-mechanical deformation, the quasi-conformality (α + β = 0) was numerically tested through multiphysics simulation (COMSOL) for 2D materials (in xy-plane) without longitudinal (z-direction) deformation28. Thus, the auxetic material with large absolute value of negative Poisson's ratio (PR, ν), which is extremely difficult to realize, is the necessary building block of STO devices based on (quasi-)conformal maps: it provides nearly zero shear strain, causing the unit cells to compress or expand virtually isotropically regardless of the deformation.

Figure 1
figure 1

Schematic and material property change induced by elastic deformation.

(a) Schematic of the elastic deformation of a unit cell. (b) The coordinate transformation between the coordinates before and after the elastic deformation. (c–d) The effective permittivity ratio generated by an elastic deformation versus the deformed area change (J = det(F)), in comparison with the quasi-conformal-mapped permittivity ratio (1/J). (c) When the dielectric constant changes as εd = 3, 10, 50 for a fixed volume fraction of fd = 0.5. (d) When volume fraction changes as fd = 0.1, 0.3, 0.5 for a fixed dielectric constant of εd = 10.

Full size image

For the derivation of smart transformation optics, it is convenient to use explicit coordinates in the original flat space and the mechanically deformed space , where the vector field is the displacement field, as described in Fig. 1b29. Displacement, or strain, enters the generalized Hooke's law, which determined the equilibrium configuration of the device given the boundary conditions and volumetric mechanical loads for the static deformations of linear elastic homogeneous isotropic materials, the complicated stress-strain relations reduce to the Cauchy-Navier equations of elasticity for displacements. The design of a transformation optical device is converted to the calculation of 2D Laplace's equations, in xy-plane, to evaluate the coordinate grids deformation during the transformation from a flat space to a distorted space 30,31. This method suggests that the calculation of the material parameters for a TO device is equivalent to the computation of spatial deformation field governed by the 2D Laplace's equation with proper boundary conditions. Starting from the elastostatic governing equation, after showing Laplace's equations of a deformed coordinate , we analytically derive the general solutions of smart TO devices by integrating transformation optics and solid mechanics.

The non-auxetic approximate smart cloak demonstrated in Ref.28, which was made of silicone rubber with a not-so-large dielectric constant (εd = 2.88), required an additional structural part (a triangular patch) at the bottom of the carpet cloak to achieve the extremely small value of the transformation Jacobian, which was necessary to realize the desired effective permittivity range for cloaking28. The deformation range for smart cloaking, defined as the range of allowed elastic deformation while it can automatically implement a valid QCM, is also limited to a narrow range. However, to achieve a versatile – and exact - smart TO device, such as, for example, a fully flexible waveguide, it is not possible to use the patch method because deformations may appear at various, unpredictable different locations in the waveguide. In addition, we would have to increase the deformable range of smart TO at the same time. Although it is known that a highly negative PR structure (ν ~ −10) with extremely high permittivity is a good candidate for smart metamaterials, it is technically very difficult to realize. Because high permittivity material is not easily available in nature, it is important to design an efficient auxetic structure that allows the highest effective permittivity out of a given dielectric material.

Here, we demonstrate a versatile smart TO device by making any range of elastic deformation automatically implement QCM without any additional structural part. We fabricated an auxetic two-dimensional (2D) plate of ν ~ −1 which enables us to achieve the maximized possible effective permittivity out of an elasto-electromagnetic metamaterial made of a specific material εd = 10.2 (PTFE ceramic, ROGERS Corp.). The extreme auxetic property (ν ~ −1) and the compressible structure without empty space allow us to create an exact, wide-deformation-range QCTO device from a single sheet of an elasto-electromagnetic metamaterial, without resorting to the patching method used in Ref. 28. Our measured 2D E-field mapping data at 7 ~ 8 GHz show that our auxetic structure has smart TO electromagnetic properties for elastic deformation, such as smart cloaking and smart arbitrary waveguiding. Using the elastostatic governing (Cauchy-Navier) equations in solid mechanics, we show that the deformed coordinates of a 2D plate, made by arbitrary elastic deformation, satisfy 2D Laplace's equations, , for specific materials of ν ~ −1 or ν ~ −∞ in plane stress or plane strain conditions, respectively. By integrating transformation optics and solid mechanics, we analytically derive the general solutions of smart TO devices.

Results

General solutions found so that elastic deformations automatically implement quasi-conformal transformations

The governing equations of elastodynamic problems of linear elastic materials are the generalized Hooke's law, σij = Cijklεkl (i, j, k, l = 1, 2, 3), that relates stress (σij) and strain (εij) with the elastic modulus tensor (Cijkl). To represent the coordinate transformation made by an elastic deformation from an original flat space Xi to the transformed space , we have to simplify the generalized Hooke's law by solving directly for the displacements (ui), instead of stress and strain. For the elastostatic deformations of a linear elastic homogenous isotropic solid with Poisson's ratio (ν) at uniform temperature (T = const), the governing equations reduce to the Cauchy-Navier equations of elasticity as following29,

where Cijkl is the elastic modulus tensor, ui displacement vector and ρ0 mass density.

If we consider a two-dimensional (2D in xy-plane) plate with finite thickness, the longitudinal (z-direction) deformation is allowed and it is represented as the well-known plane stress condition in solid mechanics 29. The mechanical loads are assumed to be constant throughout the thickness and the thickness of the plate can vary32. From Eq. (1), we obtain following two equations as explained in detail in Methods,

In the limiting case of ν → −1, , i.e., the elastic deformation always satisfies 2D Laplace's equations in xy-plane, so that . Because we use sliding boundary condition (roller boundary condition in solid mechanics) in this case, the Laplace's equation along with this proper boundary condition enables us to consider arbitrary elastic deformations equivalent to the quasi-conformal transformations30,31. By integrating TO and solid mechanics, this directly certifies that the elastic deformation (inside xy-plane) of a plate with finite thickness automatically implements quasi-conformal transformation if the material is auxetic as ν → −1 when the longitudinal deformation (z-direction) is allowed.

If we consider another 2D plate in xy-plane constrained to have no longitudinal (z-direction) deformation, it is represented by the plane strain condition in solid mechanics 29. It typically represents a cross section that cuts an infinite or very long depth such that we can ignore any end effects, in other words, a unit-depth model32. From Eq. (1), we get following relations as derived in Methods,

In the limiting case of ν → −∞, the elastic deformation satisfies 2D Laplace's equations in xy-plane, so that . This shows that the elastic deformation (inside xy-plane) of a plate automatically implements quasi-conformal transformation if the material is auxetic as ν → −∞ when the longitudinal deformation (z-direction) is not allowed.

General solutions consistently produce zero shear strains

If elastic deformation satisfy quasi-conformal transformation, shear strain is supposed to be 028, which makes shear modulus (G = shear stress/shear strain) become very large compared to bulk modulus (K). In this limiting case of for linear homogeneous isotropic materials, Young's modulus (E) and Poisson's Ratio (ν) result in . Hence, the QCM condition leads to the requirement of auxetic materials with ν ~ −1, if we allow the longitudinal deformation, i.e., plane stress condition. In our previous work, on the other hand, we considered a 2D system with longitudinal independence, constrained to the plane strain condition. For a material of given PR (ν), the effective PR under 2D plane strain constraint is derived to be , as explained in Methods. This constraint to a 2D system without longitudinal deformation requires highly negative ν such as −10 to get close to −1.

Design of optimized electromagnetic properties for auxetic TO devices

An auxetic metamaterial can be designed by employing an elastic and electromagnetic crystal, made of an incompressible dielectric material (εd) with volume fraction of fd and air or free space (εa ≈ 1). The elastic deformation can be defined by the deformation gradient tensor, and the effective permittivity ratio of this crystal after and before (εref) the deformation leads to 28. When we change the dielectric constant as εd = 3, 10, 50 for a fixed volume fraction of fd = 0.5, as presented in Fig. 1c, we plotted the effective permittivity ratio versus the deformed area change (J = det(F)), in comparison with the quasi-conformal-mapped permittivity ratio (1/J). This implies that the higher dielectric constant matches more precisely to the TO rule. On the other hand, while we change the volume fraction as fd = 0.1,0.3,0.5 for a fixed dielectric constant of εd = 10, as given in Fig. 1d, we also compared the effective permittivity ratio with the quasi-conformal-mapped permittivity ratio (1/J). This indicates that the higher volume fraction matches more precisely to the TO rule. Finally the higher permittivity and volume fraction are more desirable to realize auxetic structures which have self-adjusting TO properties for elastic deformations.

Fabrication of an auxetic structure (ν ~ −1) allowing the highest permittivity for a given material

To fabricate a real auxetic smart metamaterial sample, we used a rigid dielectric material with high permittivity of εd = 10.2 (PTFE ceramic, ROGERS Corp.). We made an array structure of a unit cell with four vertical rigid rods, alternatively cross-linked at the top and bottom, as described in Fig. 2a. If we compress (stretch) one leg among the four legs along the plane, the top joint of four legs lifts up (lowers down). Thus, all the linked four legs are going to have the same tilting angles (θ) at the side view (see Fig. 2b), resulting in a reduced (expanded) square at the top view in 2D xy-plane (see Fig. 2c). Because the lateral extension is the same as the axial extension, the cross-linked four legs can be considered as a unit cell of a 2D auxetic material of Poisson's ratio ν ~ −1 in xy-plane. To get enough range of effective permittivity variation for a TO device including a carpet cloak, we choose initial volume fraction as fd ~ 0.5 at the initial tilting angle of θ0 ~ 4° and the background permittivity of εref ~ 5. If we elastically deform the sample, the tilting angle changes from θ0 to θ and the effective permittivity of the deformed unit cell becomes where Jacobian , volume fraction , l1 the vertical length and l2 the diagonal width of a rod. Figures 2d,e are the photographs of our 200 mm × 100 mm sample with l1 = 10 mm, l2 = 1.5 mm before and after an elastic deformation. We can clearly see the auxetic behavior of our sample, especially from the movie in Supplementary Information. Because we have a realistic bottleneck to find a feasible dielectric material of high permittivity, it is important that our auxetic structure can shrink into a dielectric structure without any empty space, which enables us to achieve the maximized possible effective permittivity made of a specific material with dielectric constant of εd.

Figure 2
figure 2

Schematic and photographs of an auxetic smart TO device.

(a) Array schematic of a unit cell with four vertical rigid rods, alternatively cross-linked at the top and bottom. Right figure describes the changed shape after a shrinkage deformation induced by axial compression (green arrow in left figure). (b–c) (b) A side view and (c) a top view of a unit cell. l1, l2 are the vertical length and the diagonal width of a rod, respectively. (d–e) Photographs of our 200 mm × 100 mm auxetic sample with l1 = 10 mm, l2 = 1.5 mm (d) before and (e) after an elastic deformation.

Full size image

Experimental demonstration of a versatile smart TO device

To demonstrate a versatile TO device, our auxetic device is used in our experiments for both smart electromagnetic cloak and smart arbitrary waveguide at the same time. We place the sample in a microwave 2D E-field mapping apparatus and get the E-field mapping data of incident and scattered electromagnetic waves through our sample. We deformed our auxetic sample by a metallic bump parameterized as y = h · cos2(xπ/100) in milimetres. Figures 3a–e are the electromagnetic cloaking results for 45° incident wave, while we change the bump height (h) as h = 0 mm, 5 mm, 10 mm, 15 mm and 20 mm, respectively. When we deform the auxetic structure by a bump, it redistributes the unit cells to satisfy quasi-conformality, consistently with our theoretical prediction (see the photographs of the first column). In the E-field mapping data at 7 GHz (see the second column) and 8 GHz (see the third column), the scattered waves simply reflect and do not split for a wide range of bump heights from h = 0 mm to 20 mm, in other words, the varying bumps are electromagnetically smart-cloaked. Without an auxetic cloak, as described in Fig. 3f, a perturbation of the metallic surface (h = 10 mm) causes a strongly scattered secondary beam with a power gap in a homogeneous medium of 10 mm-thick silicone rubber plate (εd ~ 2.9) at 8 GHz.

Figure 3
figure 3

Experimentally measured E-field mapping of smart cloaking.

(a–e) Experimentally measured electromagnetic cloaking results for 45° incident wave at 7 GHz and 8 GHz, while we change the bump height (h) as (a) h = 0 mm, (b) 5 mm, (c) 10 mm, (d) 15 mm and (e) 20 mm, respectively. (f) Without an auxetic cloak, a beam incident on the bump of h = 10 mm in a homogenous medium of silicone rubber at 8 GHz. The photograph of our sample in each case is given in the first column.

Full size image

We also measured the electromagnetic wave propagation through the same auxetic sample, as presented in Figs. 4a–e, while we bend the sample at the angles of 0°, 30°, 45°, 60° and 90° between the input and output facets (see the first column). The E-field mapping data are experimentally obtained at 7 GHz (see the second column) and 8 GHz (see the third column). The phases of electromagnetic waves continuously maintain through the auxetic sample for any bending angles, i.e., “smart arbitrary waveguiding” behaviors. Figures 4f–g provide the electromagnetic wave propagation data through a homogenous waveguide made of silicone rubber medium at 8 GHz for 45° and 90° bending angles. The internally reflected waves at the boundary interfaces of the waveguide interfere with the propagating waves, which produce phase fringe patterns of wave propagations inside the waveguide. These results experimentally show that, for an auxetic metamaterial made of a high permittivity dielectric material, the elastic deformation automatically implements quasi-conformality in the broadband microwave regime.

Figure 4
figure 4

Experimentally measured E-field mapping of smart arbitrary waveguiding.

(a–e) Experimentally measured electromagnetic wave propagation through the same auxetic sample at 7 GHz and 8 GHz, while we bend the sample at the angles of (a) 0°, (b) 30°, (c) 45°, (d) 60° and (e) 90° between the input and output facets. (f–g) Without the auxetic sample, experimentally measured electromagnetic wave propagation through a homogenous waveguide made of silicone rubber at 8 GHz for (f) 45° and (g) 90° bending angles. The photograph in each case is given in the first column.

Full size image

Discussion

We have made a 2D-auxetic metamaterial structure, whose unit cell consists of four vertical rigid rods, cross-linked at the top and bottom and achieved Poisson's ratio ν ~ −1 for arbitrary deformations in the xy-plane. Since this structure exhibits smart elasto-electromagnetic behavior only when the dielectric inclusions have a very high dielectric constant, it is important to choose a geometry that minimizes empty space. Our choice of the high-index dielectric is the PTFE ceramic with εd = 10.2 (Rogers Corp.). When we deform our auxetic carpet cloak sample with variable-height metallic bumps, our measured E-field maps at 7 ~ 8 GHz indicate that the incident beam undergoes only a specular reflection without side lobes. This behavior is observed for a wide range of bump heights from h = 0 mm to 20 mm. We also measured electromagnetic wave propagation through the smart waveguide sample, while we bend the sample at the angles of 0°, 30°, 45°, 60° and 90° between the input and output facets. From the E-field mapping data at 7 ~ 8 GHz, the proper phases of electromagnetic waves are continuously maintained through the range of bending angles, i.e., the waveguide is entirely flexible. These experimental results show that, for an auxetic metamaterial made of a high permittivity dielectric material, the elastic deformation automatically implements quasi-conformality in the broadband microwave regime. The higher permittivity and volume fraction are more desirable to realize auxetic structures which have self-adjusting TO properties for elastic deformations.

In this work, using the elastostatic Cauchy-Navier equations29, we prove that the deformed coordinates of a 2D plate, made by arbitrary elastic deformations, satisfy Laplace's equations for specific materials of ν = −1 or ν = −∞ in plane stress or plane strain conditions. The Laplace's equations along with sliding boundary condition allow us to prove analytically that the elastic deformation of a plate is automatically quasi-conformal.

Methods

Derivation of Laplace's equations from elastostatic governing equations

For plane stress condition, σ33 = σ31 = σ23 = 0, and stress-strain relation is29

For plane strain condition, ε33 = ε31 = ε23 = 0, and stress-strain relation is29

Cauchy-Navier equations of motion, i.e., elastostatic equations become

  1. 1

    Plane stress configuration: σ33 = σ31 = σ23 = 0,

    If j = 1, Cauchy-Navier equations of motion become .

    When we use the relation of , it simplifies to

    For linear elastic materials, four rank (3 × 3 × 3 × 3) elastic modulus tensor Cijkl is simplified as a matrix (6 × 6) Cαβ by a relationship of (ij) → α, (kl) → β so that , respectively29. Because the matrix Cαβ consists of components from the stress-strain relations of plane stress configuration in Eq. (6), we get each coefficient as followings, , , C1131 = C15 = 0, , C2131 = C65 = 0, , C2122 = C62 = 0, C1132 = C14 = 0, C2132 = C64 = 0.

    If we insert all these coefficients into Cauchy-Navier equations, we get

    In the limiting case of ν → −1, finally we obtain 2D Laplace's equation of u1 as follows

    If j = 2, Cauchy-Navier equations become , then after simplifying with , we get

    From the stress-strain relations of plane stress configuration, we obtain each coefficient as followings, C1211 = C61 = 0, , , C2212 = C2221 = C1222 = C26 = C62 = 0, C1232 = C64 = 0, C1231 = C65 = 0, C2231 = C25 = 0, , , , C2232 = C24 = 0.

    After inserting all these coefficients into Cauchy-Navier equations, we get

    In the limiting case of ν → −1, we also get 2D Laplace's equation of u2 as follows,

  2. 2

    Plane strain configuration: , .

    For j = 1, we get coefficients of Cauchy-Navier equations, after simplifying with , as following, , , , , , , , , .

    After inserting above coefficients, the Cauchy-Navier equations finally become

    In the limiting case of ν → −∞, we obtain Laplace's equation from Eq. (14).

    For j = 2, we get coefficients of Cauchy-Navier equations, after simplifying with , as following, , , , , , , , , , .

    The Cauchy-Navier equations finally become

    In the limiting case of ν → −∞, we obtain Laplace's equation from Eq. (15).

Derivation of effective 2D Poisson's ratio in plane stress and plane strain configurations

Let's consider a planar material in xy-plane. To calculate 2D Poisson's ratio inside xy-plane, we compress the material in x-direction, i.e., σx(σ11) ≠ 0, then calculate the planar Poisson's ratio defined as .

  1. 1

    Plane stress condition

    From the stress-strain relations, we get , . Thus, the effective 2D Poisson's ratio becomes . For the plane stress condition, the effective 2D PR is the same as the Poisson's ratio of the linear elastic homogeneous isotropic material.

  2. 2

    Plane strain condition

    From the stress-strain relations, we get , . Thus, the effective 2D Poisson's ratio becomes . For the plane strain condition, the effective 2D PR is different from the Poisson's ratio of the linear elastic homogeneous isotropic material. In this case, when ν is highly negative number, such as −10, is getting close to −1.

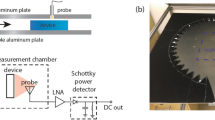
Electric field measurements

Using a phase-sensing, near-field microwave scanning system within a planar waveguide, we map the TE field distribution of the scattering region, including the incident and scattered beams. The microwaves are launched into the planar waveguide from a standard X-band coax-to waveguide coupler. The sample was tested with 7–8 GHz waves, then capturing the TE field distribution in the xy-plane.

Auxetic crystal fabrication

For a double-periodic and uniform auxetic crystal, we use PTFE ceramic (εd = 10.2, ROGERS Corp.) with 1.2 mm side length square. The ceramic was cut into slices of 10 mm length, then alternatively bonded to each other at the top and bottom using scotch wood adhesive (AD6005, 3M Corp.).