Topological modes bound to dislocations in mechanical metamaterials

Abstract

Mechanical metamaterials are artificial structures with unusual properties, such as negative Poisson ratio, bistability or tunable vibrational properties, that originate in the geometry of their unit cell^1,2,3,4,5. Often at the heart of such unusual behaviour is a soft mode: a motion that does not significantly stretch or compress the links between constituent elements. When activated by motors or external fields, soft modes become the building blocks of robots and smart materials. Here, we demonstrate the existence of topological soft modes that can be positioned at desired locations in a metamaterial while being robust against a wide range of structural deformations or changes in material parameters^6,7,8,9,10. These protected modes, localized at dislocations in deformed kagome and square lattices, are the mechanical analogue of topological states bound to defects in electronic systems^11,12,13,14. We create physical realizations of the topological modes in prototypes of kagome lattices built out of rigid triangular plates. We show mathematically that they originate from the interplay between two Berry phases: the Burgers vector of the dislocation and the topological polarization of the lattice. Our work paves the way towards engineering topologically protected nanomechanical structures for molecular robotics or information storage and read-out.

Main

Central to our approach is a simple insight: mechanical structures on length scales ranging from the molecular to the architectural can often be viewed as networks of nodes connected by links¹⁵. Whether the linking components are chemical bonds or metal beams, mechanical stability depends crucially on the number of constraints relative to the degrees of freedom. When the degrees of freedom exceed the constraints, the structure exhibits excess zero (potential) energy modes. Conversely, when the constraints exceed the degrees of freedom, there are excess states of self-stress—balanced combinations of tensions and compressions of the links, with no resultant force on the nodes. The generalized Maxwell relation¹⁶ stipulates that the index ν, given by the difference between the number of zero modes, n_m, and the number of states of self-stress, n_ss, is equal to the difference between the number of degrees of freedom, N_df, and the number of constraints, N_c,

A trivial way to position a zero-energy mode in the interior of a generic rigid lattice is to remove some bonds, locally reducing the number of constraints. Consider, instead, a network that satisfies everywhere the local isostatic condition N_df = N_c (which precludes bond removal). In this case, zero modes can be present only in conjunction with an equal number of states of self-stress, invisible partners from the perspective of motion. Isostaticity by itself, however, does not dictate how the modes are distributed spatially. Kane and Lubensky⁶ recently introduced a special class of isostatic lattices that possesses a further feature called topological polarization. Much as an electrically polarized material can localize positive and negative charges at opposite boundaries, a topologically polarized lattice can harbour zero modes or states of self-stress at sample edges (whose outward normal is respectively aligned or anti-aligned with the polarization). The edge mode distribution is biased even though both boundaries are indistinguishable on the basis of local constraint counting. Furthermore, this bias is insensitive to local variations in bond lengths, spring constants, or node masses, provided no bonds are cut and the lattice remains rigid in the bulk⁶.

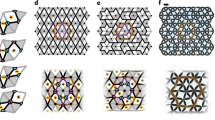
In this Letter, we harness the topological polarization to place zero modes in the interior of an isostatic lattice where topological defects called dislocations are positioned. Dislocations are termination points of incomplete lattice rows that have an edge-like character. They are characterized by a topological charge called the Burgers vector, b, which measures the deficit in any circuit surrounding the dislocation, see Fig. 1a, c. A dislocation is composed of a dipole of under-coordinated (green) and over-coordinated (orange) points (Fig. 1a) or plaquettes (Fig. 1b–d), whose orientation is obtained on rotating b by π/2. The dipole moment, d, a vector connecting the under-coordinated point/plaquette to the over-coordinated one, points outward from the added strip of material that terminates at the dislocation and has a magnitude equal to the strip width. Therefore, d quantifies the orientation and size of the effective ‘edge’ created by the dislocation.

Figure 1: Dislocations in polarized isostatic lattices.

a, Hexagonal lattice with primitive vectors {a₁, a₂}. The lattice includes an elementary dislocation, consisting of a five-coordinated point (green) connected to a seven-coordinated point (orange) in an otherwise six-coordinated lattice (blue points). The Burgers vector b = −a₂ is the deficit in a circuit (black dashed line) that would have been closed in a defect-free lattice. Rotating this vector by π/2 gives the corresponding dipole moment vector d, which connects the five-coordinated point to the seven-coordinated point. Decorating each unit cell with a three-atom basis (yellow points and magenta bonds) produces a dislocated deformed kagome lattice which contains only four-coordinated points. Three copies of the three-atom basis are shown; solid bonds connect points within the same unit cell, whereas dashed bonds connect points belonging to different cells. b, Deformed kagome lattice obtained by decorating the triangular lattice in a, thus incorporating a dislocation with the same dipole moment d. The five- and seven-coordinated points in the underlying triangular lattice translate into plaquettes bordered by five (green) and seven (orange) bonds, respectively, whereas all other points in the triangular lattice translate to plaquettes bordered by six bonds (blue) in the decorated lattice. The topological polarization P_T = a₁, calculated in ref. 6, is also shown. c, Square lattice with primitive vectors {a₁, a₂} (black arrows) which incorporates a dislocation, consisting of a three-coordinated plaquette (bordered by green bonds) adjacent to a five-coordinated plaquette (bordered by orange and green bonds), with Burgers vector b = −(a₁ + a₂). The associated dipole moment d connects the three- and five-coordinated plaquettes. d, Decorating each point in c with the four-point unit cell (yellow points and magenta bonds) gives a distorted square lattice which incorporates a dislocation of the same dipole moment, and has a non-zero topological polarization P_T = a₁ − a₂.

To localize topological modes at these effective edges, we need to incorporate the dislocations into polarized lattices without modifying the local constraint count (that is, trivial zero modes must be excluded). We demonstrate this construction for two polarized lattices: a deformed kagome lattice introduced in ref. 6 and a deformed square lattice. As shown in Fig. 1, both lattices are obtained by decorating a 2D crystal lattice (regular hexagonal and square, with primitive vectors {a₁, a₂} indicated in Fig. 1a, c, respectively) with a multi-atom basis at each unit cell. In the absence of defects, the unit cell determines the topological polarization P_T of the bulk lattice. In the Supplementary Information we show that P_T = a₁ − a₂ for the deformed square lattice; it has been shown in ref. 6 that P_T = a₁ for the deformed kagome lattice. Dislocations in the undecorated lattice carry over to the polarized lattice and, when appropriately chosen, produce a lattice that is four-coordinated everywhere (Fig. 1b, d). See the Supplementary Information for more details of the construction.

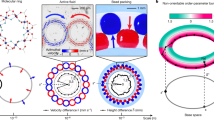
Having constructed polarized lattices with dislocations, we numerically compute their vibrational spectrum by treating each bond as a harmonic spring. Results are shown in Fig. 2a, b for deformed kagome and square networks, respectively. We use periodic boundary conditions, which preserves isostaticity everywhere but requires a net Burgers vector of zero. As a result, dislocations appear in pairs with equal and opposite dipole moments. In both networks, the dipole moments of the dislocation on the left (d_L = a₁ − a₂) and on the right (d_R = − d_L) are aligned, respectively, with and against the lattice polarization. The left dislocation has an associated soft mode in both cases, labelled by arrows, whose energy decreases with system size. The opposite dislocation is associated with an approximate state of self-stress, labelled by coloured and thickened bonds following ref. 6. See Supplementary Information for computational details. These observations are consistent with the intuitive interpretation of dislocations as edges oriented by their dipole moment.

Figure 2: Mechanical modes localized at defects.

a, Visualization in a deformed kagome lattice of a numerically obtained low-energy soft mode (red arrows, showing the direction, with lengths and thicknesses scaled by the relative amplitude of allowed displacements) and an approximate state of self-stress (thickened bonds, showing bond forces in magenta (+) and blue (−) that cancel each other) associated with a pair of dislocations with equal and opposite dipole moments d_L and d_R (dashed arrows). The dislocations are in the interior of a lattice with periodic boundary conditions that is perfectly isostatic. Only a small region of the lattice is shown. Each dislocation consists of a five-coordinated plaquette (enclosed by green triangles) adjacent to a seven-coordinated plaquette (enclosed by green and orange triangles). b, Section of a deformed square lattice of a numerically obtained low-energy soft mode and a state of self-stress associated with a pair of dislocations with equal and opposite dipole moments d_L and d_R. The visualization method is similar to that in a. The dislocations are in the interior of a lattice with periodic boundary conditions that is perfectly isostatic. Each dislocation consists of a three-coordinated plaquette (enclosed by cyan plaquettes) near a five-coordinated plaquette (enclosed by cyan and yellow plaquettes). All other plaquettes are four-sided. c, Plastic prototype of a deformed kagome network, built as described in the text. The interior contains two dislocations which reproduce the configuration from the computer model shown in a. Scale bar, 5 cm. Inset: superposition of three configurations that span the range of the free motion associated with the left dislocation.

To assess whether these modes can be observed in metamaterials with realistic bonds, joints and boundary conditions, we have built prototypes of the deformed kagome lattice, composed of rigid triangles laser-cut out of 3 mm thick PMMA sheets. The corner of the triangles are connected by plastic bolts that act as hinges. The boundary points are pinned to a flat base by screws, but can pivot freely. The design ensures that each internal vertex has as many constraints as degrees of freedom, satisfying the local isostatic condition away from the boundary. Figure 2c shows such a prototype mimicking the dislocation configuration of the computer model from Fig. 2a. Theoretically, the boundary pinning and the use of rigid triangles push the phonon gap to infinity, so that only zero modes can be observed. In practice, the prototype has some compliance and mechanical play at the pivots. Nonetheless, it is rigid in the bulk, as can be verified by unsuccessfully trying to move the (white) triangles far from the dislocations, see Supplementary Movie 1.

Despite the differences between the two systems, the soft mode observed in the simulated harmonic network survives in the real-world prototype as a collective motion of points near the left dislocation. The motion is easily activated by pushing the hinge joints of the triangles that make up the dislocation (inset to Fig. 2c and Supplementary Movie 2). The motion is not a strict zero mode because it interacts with the pinned boundary of the finite system, but the structural compliance is sufficient for the remnant soft motion to be observed. In contrast, the dislocation on the right does not admit displacements in its vicinity and remains rigid (Supplementary Movie 3), consistent with the simulations.

To quantify the number and type of modes associated with a dislocation, an electrostatic analogy proves useful. Once the connectivity of a locally isostatic lattice is fixed, the index ν in equation (1) can be viewed as a topological charge, invariant under smooth deformations of the lattice. Just as the Gauss law yields the net charge enclosed in a region from the flux of the electric polarization through its boundary, the net value of ν in an arbitrary portion of an isostatic lattice is given by the flux of the topological polarization through its boundary⁶. On evaluating the flux of P_T on a contour encircling an isolated dislocation, we obtain

where V_cell is the unit cell area. In the Supplementary Information, we present a detailed derivation of equation (2) that accounts for the elastic strains around the dislocation. Here, we simply comment on its physical interpretation.

The topologically protected modes arise from a delicate interplay between a Berry phase associated with cycles in the Brillouin zone, embedded in P_T (ref. 6), and the Berry phase of a topological defect in real space, represented by its Burgers vector (or dipole d). A similar interplay dictates the existence of localized electronic modes at dislocations in conventional topological insulators^12,13. Equation (2) gives ν = +1 (−1) for the left (right) dislocation in the deformed kagome lattice, and ν = +2 (−2) in the deformed square lattice. The sign of ν distinguishes zero modes (+) from states of self-stress (−), while its magnitude gives their numbers. For instance, we correctly predict that the square lattice of Fig. 2b admits two soft modes localized to the left dislocation (as verified in Supplementary Fig. 1).

The soft modes investigated here have unusual localization properties, as shown in Fig. 3. The mode amplitude falls off exponentially along most rays originating at the core of the left dislocation, but the decay length depends on the direction of the ray relative to the underlying lattice. There are two special directions in each lattice (one of which is highlighted by red circles in both Fig. 3a, b) along which the localization is weak. In all other directions, the mode decays over much shorter length scales, of the order of a few lattice constants (green circles and symbols in Fig. 3). In the Supplementary Information, we show that the weak localization directions track lines in momentum space along which the acoustic modes vary quadratically, rather than linearly, with the momentum. The localization of the approximate state of self-stress behaves similarly, with weak directions that are the opposite of those for the soft mode.

Figure 3: Anisotropic localization of the soft mode.

a, Amplitude of the soft mode associated with the left dislocation in the kagome lattice shown in Fig. 2a, visualized as blue disks whose area is scaled by the displacement magnitude at each lattice point. The dipole moment vectors d_L and d_R (solid arrows) indicate the position and orientation of the dislocations. Inset: soft mode amplitude as a function of distance from the left dislocation, along two directions (indicated by red and green circles in the main panel which enclose the lattice points sampled in the red and green curves, respectively). b, Same as in a for the soft mode associated with the left dislocation shown in Fig. 2b.

The topologically protected modes we have identified could have applications across a wide range of systems and length scales. At macroscopic scales, isostatic origami structures exist whose deformations are restricted to rotations of hinged triangles, much as in the kagome lattice¹⁷. At the microscale, dislocations could be used for robust information storage, with a bit encoded by the presence (+) or absence (−) of a topological soft mode, in turn controlled by the orientation of the Burgers vector. Such protected bits could be hard-wired into microscopic ‘punch cards’ that could be read out mechanically by probing the region around dislocations for soft motions (or lack thereof). We also envisage molecular robots and smart metamaterials that could exploit the protected modes as activated mechanisms.