Main

In a solid the behaviour of the electrons is most fully described in terms of the electron Green’s function, the poles of which map the energy versus momentum dependence of the electronic quasiparticles (the dressed electronic states)5. The locus of poles at the Fermi energy, EF, defines the Fermi surface of the material, from which almost all of the electronic properties of a material emanate. For a single continuous band, the Fermi surface should form a continuous loop. Consequently, the broken segments of Fermi surface known as Fermi arcs apparently require a major rethinking of some of the basic tenets of condensed matter physics.

One approach to resolve this problem is completely discarding the notion of electron quasiparticles, and with it almost all of the understanding of solids built up from generations of condensed matter physicists. Much support for this line of reasoning came from angle-resolved photoemission spectroscopy (ARPES), which is unique in its ability to directly probe the electronic excitations as a function of energy and momentum, that is the quasiparticles. Earlier ARPES studies found that the ARPES peaks were either anomalously broad or vanishingly weak11,12,13 especially in the underdoped ‘pseudogap’ regime of the cuprates—aspects that were widely taken as evidence for the lack of electron-quasiparticles. The recent introduction of laser and low-energy14 ARPES made tremendous advances in the peak sharpness and spectral weight at EF, handicapping this line of argument. We, for example, now see sharp nodal quasiparticle-like peaks for all doping levels of Bi2Sr2CaCu2O8+δ (Bi2212) studied (down to moderately underdoped x=0.10 samples), in contrast to recent studies which were unable to observe peaks below x=0.20 (ref. 13). Therefore other ideas are needed to understand the origin of the unusual non-Fermi liquid behaviour in the cuprates. Here we show that regardless of whether the peaks are sharp enough to be considered quasiparticles, these states do not reach the Fermi energy and so cannot dominate the transport and thermodynamics in the way that regular quasiparticle states normally would. This finding reduces the relevance of the question of whether these states are sharp enough to be quasiparticles. Instead, we argue that a more relevant issue in understanding the nature of the non-Fermi liquid behaviour is whether these excitations reach the Fermi energy at all.

As well as its ability to measure quasiparticle peaks, the momentum-resolution of ARPES makes it a preferred tool to study gaps and Fermi surfaces, and therefore Fermi arcs. Despite its great power and directness, ARPES has lacked appropriate quantitative analysis techniques, which can also significantly affect the qualitative picture that emerges. For example, gap values have been predominantly measured using the approximate ‘midpoint of leading edge’15 or ‘peak separation of symmetrized spectra’1,2 techniques, each of which is known to fail in many limits. Phenomenological models16 have also been used to fit gapped energy distribution curves17 (EDCs), but because the EDC lineshape is not yet understood18, these fittings are not obviously better than the approximate measures.

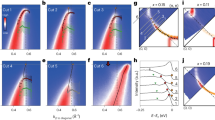
To avoid the difficulties inherent in the traditional techniques of analysing ARPES spectra, we have developed and employed a new method, the tomographic density of states (TDoS), the creation of which is illustrated in Fig. 1 (with more details in the Supplementary Information). Briefly, the TDoS is a one-dimensional momentum sum19 of the coherent electronic spectral weight (black curve in Fig. 1d), which is then normalized to a similar but ungapped reference momentum sum along the node (black curve in Fig. 1b), with some similarities to the proposal present in ref. 19. The resulting TDoS (Fig. 1f) represents the density of states and is in many ways equivalent to a typical Giaever tunnelling curve of an s-wave superconductor20, except that it is localized to a single slice through the band structure (hence the name tomographic, meaning sliced or sectioned). This unique advantage is indispensible when electron interactions are strongly momentum dependent (for example, in a d-wave superconductor).

Figure 1: Creation and fitting of the TDoS.
figure 1

a, Nodal spectrum of optimally doped (Tc=92 K) Bi2212 at T=50 K, taken along the yellow cut in the Brillouin zone inset to the figure. b, The coloured curves represent 7 out of a total of 170 individual EDCs taken along the corresponding horizontal coloured lines of a. The green EDC corresponds to k=kF. The sum of all 170 individual EDCs gives the spectral weight curve (black). c, Slightly (6°) off-nodal spectra taken along the red cut in the Brillouin zone inset. d, EDCs and the corresponding spectral weight for the data of c showing the superconducting gap at EF as well as the additional spectral weight above EF due to the Bogoliubov quasiparticles. e, Off-nodal spectra normalized to nodal spectral weight (colour scale data) and the spectral weight curves from b and d (orange and red curves, respectively). The red curve is normalized to the orange curve to create the TDoS curve (yellow). f, Fit of the TDoS (red circles) to the Dynes tunnelling formula (green line).

Full size image

To analyse the TDoS, we use the formula first proposed by Dynes to explain tunnelling spectra from strongly coupled s-wave superconductors:

where ITDoS is the TDoS intensity, ω is the energy relative to EF, ΓTDoS is the pair-breaking scattering rate and Δ is the superconducting gap21. This formula is essentially a simple Bardeen–Cooper–Schrieffer density of states with gap Δ, broadened by the parameter ΓTDoS, which is interpreted as the rate of pair-breaking. This formula has been extensively tested on conventional superconductors23 and, although initially phenomenological, it has been derived from the Eliashberg theory22. As each TDoS is specific to a single location on the Fermi surface, the gap magnitude is single valued, allowing us to use Dynes’ original form even in d-wave superconductors. An example fit of a TDoS to equation (1) is shown in Fig. 1f, with the extracted superconducting gap value Δ=5.9±0.1 meV and scattering rate ΓTDoS=2.6±0.1 meV. The ΓTDoS values extracted here are consistent with what has been measured by tunnelling24 and optics25, although previous ARPES-based methods to extract electronic scattering rates relied on EDC or Momentum Distribution Curve (MDC) widths that give values roughly an order of magnitude larger26—see, for example, the EDCs of a, which have widths of order 20 meV. This difference arises because ΓTDoS is sensitive only to pair-breaking interactions whereas the EDCs and MDCs are sensitive to all electronic scattering processes (see Supplementary Fig. SM3).

Taking advantage of the momentum selectivity of the TDoS, Fig. 2 details the evolution of the TDoS along the Fermi surface in the near-nodal regime from an optimally doped (Tc=91 K) Bi2212 sample. By fitting to the Dynes formula, equation (1), we find the gap is linear and symmetric about the node, as expected for a d-wave gap (Fig. 2e). In this near-nodal regime, ΓTDoS is essentially isotropic and of the scale of 2–3 meV, which is counter to earlier ARPES observations in which Γ was large (of the order of 20–30 meV) and grew rapidly away from the node26.

Figure 2: Angular dependence of the TDoS and comparison with conventional ARPES analysis techniques from an optimal Tc=91 K Bi2212 sample at T=50 K.
figure 2

a, Angle dependence of ARPES spectra, colour coded according to location in the Brillouin zone, as indicated in the inset. c,d follow the same colour coding, as do the positive angular labels of a. b, TDoS curves versus angle. c, EDCs at kFversus angle. d, Symmetrized EDCs at kF versus angle, all from the same data set. e, ΔTDoS and ΓTDoS for angles very near the node. Error bars are ±σreturned from fits to the data of b. f, ΔTDoS near the node compared against values of Δ measured by the other two methods. These other methods show a short but artificial ‘arc’ of zero-gapped states near the node, whereas ΔTDoS extrapolates to 0 meV only at the node.

Full size image

In Fig. 2f, we compare the TDoS gap measurements with the EDC leading edge15 technique (data in Fig. 2c) and symmetrized EDC (refs 1, 2) technique (Fig. 2d), all of which came from the identical ARPES data sets. We show ΔTDoS is roughly the average of the ‘standard’ techniques away from the node. However, the other methods both fail in proximity to the node. Specifically, both the EDC leading edge method and the symmetrized EDC methods have a short ‘arc’ near the node, in which the extracted gap value is either zero or negative (which is often artificially set to zero). Directly observing the sharp cusp of the d-wave gap so near the node confirms the findings of other probes such as thermal conductivity27. By comparing Fig. 2e,f we see that the threshold for the artificial zero gap in the conventional techniques is when ΓTDoS≈Δ. This zero-gap regime is what previously would have been considered a Fermi arc—that is, the zero gap regime would have indicated the presence of a real portion of the Fermi surface2.

To study the Fermi arc in greater detail we move to an underdoped sample (Tc=65 K) with finely gridded momentum maps in the superconducting state (T=10 K) and the normal (that is, pseudogap and/or pre-pairing) state (T=75 K; Fig. 3). The formation of the Fermi arc is evident in the Fermi surface maps (Fig. 3a). The symmetrized EDCs show a small (2°) Fermi arc at 10 K but a much larger one at 75 K, with a gap from this method (determined by the depression of weight at zero energy) only definitively present at 10° and beyond (Fig. 3b). However, the TDoS paint a different picture, showing a smooth evolution of the gap rather than a discrete change at any one angle (Fig. 3c). Our observation of a finite near-nodal gap above Tc is only possible if there are pre-formed superconducting pairs in the pseudogap state28,29.

Figure 3: Comparing the TDoS and symmetrized EDCs when determining a Fermi arc, for an underdoped (Tc=65 K) sample.
figure 3

a, Spectral weight at EF both in the superconducting (T=10 K, top) and pseudogap (T=75 K, bottom) states. b, Symmetrized EDCs from which one would determine a finite range of gapless states at EF that grows with increasing temperature. The colour coding of spectra from all panels follows the angular legend shown in this panel. c, Measured TDoS spectra as a function of angle away from the node. d, Two parameter fits (ΓTDoS and ΔMax) for each entire set of spectra, with parameters listed on the panels. ΔMax is the maximum of the d-wave gap, occurring at the antinode, with the k-dependence of the gap forced to maintain the simple d-wave form. ΓTDoSis held to a constant value throughout k-space, consistent with the results of Fig. 2e.

Full size image

Assuming a simple d-wave Δ and an isotropic ΓTDoS, we can fit the entire momentum dependence of the TDoS at once (Fig. 3d). Both the superconducting and pseudogap states may be fitted well with this form. Whereas ΔMax has shrunk by 30% from the superconducting state to the normal state, ΓTDoS has more than doubled, completely filling in the gap for states close to the node. These filled-in states are the source of previous observations of a Fermi arc and should be considered a manifestation of superconductive pre-pairing in the pseudogap state. The extremely short arc in the superconducting state is most probably due to in-plane impurity scattering (for example, Cu vacancies)30,31. However, the growth of the arc with temperature cannot be explained by static disorder. Instead, a dynamical process must lead to the increased pair-breaking rate that causes the arc to grow10, as was first proposed in ref. 10.

A more complete temperature dependence of the Fermi arc is shown in Fig. 4a, for a similarly underdoped sample (Tc=67 K). The growth of the Fermi arc with temperature2 can be accurately simulated with an electron Green’s function which uses a tight-binding band structure obtained from experiment, a simple d-wave gap (ΔMax=38 meV), and a scattering rate ΓTDoS which is constant across the Fermi surface (Fig. 2e) but which varies strongly with temperature. The values of the electron scattering rate are directly obtained from the Dynes fits up to 110 K. At higher temperatures the fits become less reliable, so we have extrapolated those values. Although the gap is seen to close slightly with increasing temperature (Fig. 3d), it was held constant in Fig. 4 for simplicity. The observed growth of the Fermi arc with increased temperature can be understood with the aid of the schematic of Fig. 4b. As the dominant effect of raising temperature is to increase ΓTDoS, the threshold of ΓTDoS=Δ moves away from the node, increasing the arc length.

Figure 4: Simulating the observed temperature dependence of the Fermi arc from a Tc=67 K underdoped Bi2Sr2CaCu2O8 sample.
figure 4

a, The unusual temperature-dependent arc length is seen in both the data and simulations. The main inputs to the simulations are an experimentally determined tight-binding band structure, a simple dwave gap (both below and above Tc) with independently measured d-wave gap maximum 40 meV, and a temperature-dependent scattering rate ΓTDoS (shown) with units of meV. The majority of these ΓTDoS values (<110 K) are also independently experimentally determined. b, Simple picture for the temperature dependence of the Fermi arc length. The arc is approximately the region where ΓTDoS>Δ, which grows rapidly with temperature as ΓTDoS grows. c, Diagram showing the change in spectral weight (red) along the Fermi surface due to increasing ΓTDoS between the superconducting and normal states, as determined by the TDoS (green).

Full size image

The notion of discontinuous Fermi arcs put forward from the previous ARPES experiments is unphysical within the context of standard condensed matter theory, because Fermi surfaces must be topologically connected. Therefore, a great effort has been made to observe if and how these arcs close to form a Fermi pocket. For example, recent ARPES experiments6,7 have presented evidence for arc closures, although many of these have been met with scepticism for reasons such as including potential contamination from shadow bands, superstructure bands9, or extended extrapolations. With the understanding presented here, there is no physical reason why the arc would need to be closed, because it is not a real locus of quasiparticle states. In this light, the difficulty in observing the ‘back’ side of the arc is completely natural—that is, the arc is actually arc-like, as opposed to only being the front side of a small hole pocket.

High magnetic field quantum oscillation studies in the cuprates have found evidence for a small Fermi surface pocket8, with these pockets potentially related to the pockets discussed in some of the ARPES experiments. However, Hall effect measurements indicate that the pockets hold electrons instead of holes8, making it clear that the pockets observed in the quantum oscillation experiments are inconsistent with the ARPES Fermi arc with back-side closure. Furthermore, new evidence from nuclear magnetic resonance experiments indicates that the high magnetic fields used in the quantum oscillation experiments cause a reconstruction of the Fermi surface that can create the small pockets observed in those experiments32.

Within the conventional analysis method of symmetrized EDCs, the Fermi arcs are considered loci of quasiparticle states at the Fermi level that grow with increasing temperature. Instead, the above simulations and data argue that the arcs are a result of the interplay between Δ(k,T) and ΓTDoS(k,T), which we find is dominated by Δ(k) and ΓTDoS(T). Importantly, this result indicates that the arcs are not composed of true quasiparticles, because, even though the quasiparticles exist, they are not at at EF—rather the pole locations are the gap values, Δ(k) (Fig. 4c). Rather than a true Fermi surface of quasiparticle poles, the arcs are regions where real spectral weight has been scattered inside the d-wave gap, with this incoherent non-quasiparticle weight varying with Fermi surface angle and temperature (Fig. 4c). Aside from the single quasiparticle state at the node, this non-quasiparticle weight comprises the only states available to contribute to the low-energy transport and thermodynamic properties. Therefore, these states are strong candidates to explain the unusual transport, heat capacity, and other thermodynamic properties in the pseudogap state of the cuprates33.