Main

In cavity quantum electrodynamics (QED), a two-level atom interacts with the quantized modes of an optical or microwave cavity. The information on the coupled system is encoded both in the atom and in the cavity states. The latter can be accessed spectroscopically by measuring the transmission properties of the cavity16, whereas the former can be read out by suitable detectors18,19. In circuit QED, the solid-state counterpart of cavity QED, the first category of experiments was implemented by measuring the microwave radiation emitted by a resonator (acting as a cavity) strongly coupled to a charge qubit8. In a dual experiment, the state of a flux qubit was detected with a d.c. superconducting quantum interference device (SQUID) and vacuum Rabi oscillations were observed10. More recently, both approaches have been exploited to extend the toolbox of quantum optics on a chip11,12,13,14,15,22. Whereas all of these experiments use one-photon driving of the coupled qubit–resonator system, multiphoton studies are available only for sideband transitions15 or bare qubits3,4,5,6,7. The experiments discussed here explore, to our knowledge for the first time, the physics of the two-photon-driven Jaynes–Cummings dynamics in circuit QED. In this context, we show that the dispersive interaction between the qubit and the two-photon driving enables real level transitions. The nature of our experiment can be understood as an upconversion mechanism, which transforms the two-photon coherent driving into single photons of the Jaynes–Cummings dynamics. This process requires energy conservation and a not-well-defined parity21 of the interaction hamiltonian owing to the symmetry breaking of the qubit potential. Our experimental findings reveal that such symmetry breaking can be obtained either in a controlled way by choosing a suitable qubit operation point or by the presence of spurious fluctuators23.

The main elements of our set-up, shown in Fig. 1a,b, are a three-Josephson-junction flux qubit, a resonator made of an inductor L and a capacitor C (L C resonator), a d.c. SQUID and a microwave antenna24,25. The qubit is operated near the optimal flux bias Φx=1.5Φ0 and can be described with the hamiltonian , where and are Pauli operators. From low-level microwave spectroscopy, we estimate a qubit gap Δ/h=3.89 GHz. By changing Φx, the quantity ε≡2Ip(Φx−1.5Φ0) and, in turn, the level splitting can be controlled. Here, ±Ip are the clockwise and anticlockwise circulating persistent currents associated with the eigenstates |±〉 of . Far from the optimal point, |±〉 correspond to the eigenstates |g〉 and |e〉 of . The qubit is inductively coupled to a lumped-element L C resonator10, which can be represented by a quantum harmonic oscillator (see the Methods section), , with photon number states |0〉, |1〉, |2〉, and boson creation and annihilation operators and respectively. This resonator is designed such that its fundamental frequency, ωr/2π=6.16 GHz, is largely detuned from Δ/h. The qubit–resonator interaction hamiltonian is , where g=2π×115 MHz is the coupling strength. The L C circuit also constitutes a crucial part of the electromagnetic environment of the readout d.c. SQUID. In this way, the flux signal associated with the qubit states |±〉 can be detected while maintaining reasonable coherence times and measurement fidelity24,25.

Figure 1: Experimental architecture and theoretical model.
figure 1

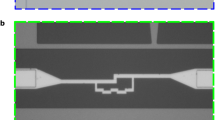
a, The flux qubit (red, junctions marked by crosses) is inductively coupled to the readout d.c. SQUID (black rectangle), which is shunted by an L C circuit acting as a quantized resonator (blue)10. All elements within the shaded area are at a temperature T≃50 mK. Microwave signals and flux-shift pulses are applied via an onchip antenna (green). The signal-to-noise ratio is improved by cold attenuators. b, Scanning electron micrograph of flux qubit and readout d.c. SQUID. c, Pulse scheme for qubit microwave spectroscopy with the adiabatic shift pulse method. First, the qubit is biased at a suitable readout point (Φx≠1.5Φ0) using a superconducting coil and initialized in the ground state |g〉. Then, the qubit is shifted to the operation point with a rectangular adiabatic shift pulse (green). There, it is irradiated with a 100 ns microwave pulse (green). Finally, the qubit state is detected by measuring at the readout point applying a pulse to the d.c. SQUID measurement lines. Averaging yields the probability Pe to find the qubit in the excited state |e〉. Our protocol enables qubit-state detection also at the optimal point24 despite a vanishing mean value . d, Upconversion dynamics describing the physics governing our experiments, see equation (1). The qubit (red) level splitting is ℏωq and the resonator (blue) frequency is ωr/2π. In the relevant case of two-photon driving with frequency ω/2π (green), the system predominantly decays via the resonator. The qubit–resonator coupling strength is . For Φx≠1.5Φ0, the mirror symmetry of the qubit potential (red double well; x axis: phase variable ) is broken enabling two-photon transitions.

Full size image

To probe the properties of our system, we carry out qubit microwave spectroscopy using an adiabatic shift pulse technique24,25 (Fig. 1c). The main results are shown in Fig. 2a,b. First, there is a flux-independent feature at approximately 6 GHz due to the resonator. Second, we observe two hyperbolas with minima near 4 GHz≃Δ/h and 2 GHz≃Δ/2h, one with a broad and the other with a narrow linewidth. They correspond to the one-photon (ω=ωq) and two-photon (2ω=ωq) resonance condition between the qubit and the external microwave field. In addition, the signatures of two-photon-driven blue-sideband transitions are partially visible. One can be attributed to the resonator, |g,0〉→|e,1〉, and the other to a spurious fluctuator23. We assume that the latter is represented by the flux-independent hamiltonian and coupled to the qubit via , where and are Pauli operators. Exploiting the different response of the system in the anticrossing region under one- and two-photon driving, as explained in Fig. 2a, the centre frequencies of the spectroscopic peaks can be accurately fitted to the undriven hamiltonian . Setting (see the Methods section), we obtain g/2π=115 MHz, , Ip=367 nA, and , where .

Figure 2: Qubit microwave spectroscopy: data and simulations.
figure 2

a, Centre frequency of the measured absorption peaks (symbols) plotted versus the flux bias. The lines are fits of the undriven hamiltonian to the data. The presence of a large (ω≈ωr) and small (2ω≈ωr) anticrossing constitutes direct evidence that two-photon spectroscopy selectively drives the qubit (but not the resonator), thereby probing the vacuum Rabi coupling g. On the contrary, the one-photon driving populates the cavity resulting in an enhanced coupling . b, Measured probability Pe to find the qubit in the excited state plotted versus flux bias and driving frequency (black rectangle: area shown in Fig. 3a). c, Simulated probability Pe obtained with the time-trace-averaging method for the driven hamiltonian (black rectangle: area shown in Fig. 4). Taking Pe as the average over a full 100 ns time trace consisting of 10,000 time points gives excellent agreement with the experimental data of b. No terms describing dissipation are included; the linewidth of the peaks is caused by power broadening. Simulation parameters are derived from the fit in a. The used inductance values are based on numerical estimates.

Full size image

Further insight into our experimental results can be gained by numerical spectroscopy simulations based on the driven hamiltonian . Here, , and represent the driving of the qubit, resonator and fluctuator respectively. We approximate the steady state with the time average of the probability Pe to find the qubit in |e〉 (time-trace-averaging method). Inspecting Fig. 2c, we find that for the driving strengths Ω/h=244 MHz, η/h=655 MHz and , our simulations match well all of the experimental features discussed above. Using η and the relation for the steady-state mean number of photons of a driven dissipative cavity, we estimate a cavity decay rate κ≃210 MHz. This result is of the same order as κ≃400 MHz estimated directly from the experimental linewidth of the resonator peak. The large κ is due to the galvanic connection of the resonator to the d.c. SQUID measurement lines (Fig. 1a).

To elucidate the two-photon driving physics of the qubit–resonator system, we consider the spectroscopy data near the corresponding anticrossing shown in Fig. 3a. For 2ω=ωq=ωr, the split peaks cannot be observed directly because the spectroscopy signal is decreased below the noise floor δ Pe≃1–2%. This results from the fact that the resonator cannot absorb a two-photon driving and its excitation energy is rapidly lost to the environment (κ>g/2π). In contrast, for the one-photon case (ω=ωq=ωr), there is a driving-induced steady-state population of  photons in the cavity. Accordingly, the one-photon peak height shows a reduction by a factor of approximately two, whereas the two-photon peak almost vanishes, see Fig. 3b. To support this interpretation, we compare the simulation results from the time-trace-averaging method to those obtained with the standard Lindblad dissipative-bath approach (Fig. 3c–f). In the latter case, the role of qubit decoherence and resonator decay can be studied explicitly solving a master equation22. The simulation results of Fig. 3c–f prove that the two-photon peak indeed vanishes because of the rapid resonator decay, but not because of qubit decoherence. Altogether, our experimental data and numerical simulations constitute clear evidence for the presence of a qubit–resonator anticrossing under two-photon driving.

Figure 3: Qubit microwave spectroscopy close to the qubit–resonator anticrossing under two-photon driving: data and simulations.
figure 3

a, Measured probability Pe to find the qubit in |e〉 plotted versus flux bias and driving frequency (black rectangle: area of simulations in c and e; solid lines: fit to ). b, Maximum height of the spectroscopy peaks under one-photon and two-photon driving plotted versus the flux bias (solid lines: guides to the eye). c, Simulated probability Pe (time-trace-averaging method, no dissipation, parameters as in Fig. 2c), revealing an anticrossing signature. d, Green curve: split-peak profile of Pe along the vertical line in c. Blue curve: single-peak result obtained for the same flux bias and g=0. e, Simulated probability Pe using the Lindblad formalism22 neglecting the spurious fluctuator (dissipation: qubit relaxation rate γ1=3.3 MHz, qubit dephasing rate γϕ=67 MHz, resonator quality factor Q≡ωr/κ=2π×6.16 GHz/400 MHz≃100). When qubit and resonator become degenerate, the spectroscopy signal fades away. f, Green curve: split-peak profile of Pe along the vertical line in e. Blue line: single-peak result obtained for the same flux bias and g=0. Differently from the non-dissipative case (c and d), the split-peak amplitudes are reduced by a factor of 10 compared with the single peak. This demonstrates that the vanishing two-photon spectroscopy signal observed in the experimental data (see a, b and e) is not caused by qubit decoherence.

Full size image

The second-order effective hamiltonian under two-photon driving can be derived using a Dyson-series approach (see the Methods section). Starting from the first-order-driven hamiltonian and neglecting the cavity driving and the fluctuator because of large-detuning conditions, we obtain

where and are the qubit raising and lowering operators respectively, sinθ≡Δ/ωq and cosθ≡ε/ωq. The upconversion dynamics shown in Fig. 1d is clearly described by equation (1). The first two terms represent the qubit and its coherent two-photon driving with angular frequency ω. The last two terms show the population transfer via the Jaynes–Cummings interaction to the resonator. The Jaynes–Cummings interaction in this form is valid only near the anticrossings (, ; see the Methods section). As discussed before, the resonator will then decay emitting radiation of angular frequency 2ω.

The model outlined above enables us to unveil the symmetry properties of our system. Even though the two-photon coherent driving is largely detuned, ωq/2=ω≫(Ω/2)sinθ, a not-well-defined symmetry of the qubit potential permits level transitions away from the optimal point. Because of energy conservation, that is, frequency matching, these transitions are real and can be used to probe the qubit–resonator anticrossing. The effective two-photon qubit driving strength, (Ω2sin2θ/4Δ)cosθ, has the typical structure of a second-order dispersive interaction with the extra factor cosθ. The latter causes this coupling to disappear at the optimal point. There, the qubit potential is symmetric and the parity of the interaction operator is well defined. Consequently, selection rules similar to those governing electric dipole transitions hold21. This is best understood in our analytical two-level model, where the first-order hamiltonian for the driven diagonalized qubit becomes at the optimal point. In this case, one-photon transitions are allowed because the driving couples to the qubit via the odd-parity operator . In contrast, the two-photon driving effectively couples via the second-order hamiltonian . As is an even-parity operator, real level transitions are forbidden (see the Methods section). We note that the second term of renormalizes the qubit transition frequency slightly and can be neglected in equation (1), which describes the real level transitions corresponding to our spectroscopy peaks. The intimate nature of the symmetry breaking resides in the coexistence of and operators in the first-order hamiltonian , which produces a non-vanishing term in the second-order hamiltonian of equation (1). This scenario can also be realized at the qubit optimal point by the fluctuator terms and . As shown in Fig. 4, their presence causes a revival of the two-photon signal and the discussed strict selection rules no longer apply. Accordingly, we observe only a reduction instead of a complete suppression of the two-photon peaks near the qubit optimal point in the experimental data of Fig. 2b.

Figure 4: Two-photon spectroscopy simulations close to the optimal point using the time-trace-averaging method.
figure 4

a, Probability Pe to find the qubit in |e〉 plotted versus driving frequency and flux bias (parameters as in Fig. 2c; in particular, the fluctuator parameters are and ). The spectroscopy signal vanishes completely at the optimal point, Φx=1.5Φ0, because of the specific selection rules associated with the symmetry properties of the hamiltonian21. b, Same as in a, but for and . Here, the coexistence of the flux-independent first-order and terms of the fluctuator gives rise to a non-vanishing second-order term even at the qubit optimal point. The presence of the fluctuator breaks the symmetry of the total system at the optimal point and parity becomes not well defined. Consequently, the spectroscopy signal is partially revived. In reality, an ensemble of fluctuators with some distribution of frequencies and coupling strengths rather than a single fluctuator is expected to contribute to the symmetry breaking. Furthermore, when the experimental resolution is limited, a single peak will be detected instead of the detailed structure of b. This is the case in our measurements (Fig. 2b).

Full size image

In summary, we use two-photon qubit spectroscopy to study the interaction of a superconducting flux qubit with an L C resonator. We show experimental evidence for the presence of an anticrossing under two-photon driving, enabling us to estimate the vacuum Rabi coupling. Our experiments and theoretical analysis shed new light on the fundamental symmetry properties of quantum circuits and the nonlinear dynamics inherent to circuit QED. This can be exploited in a wide range of applications such as parametric upconversion, generation of microwave single photons on demand11,26,27 or squeezing28.

Methods

Two-photon-driven Jaynes–Cummings model via Dyson series

We now derive the effective second-order hamiltonian describing the physics relevant for the analysis of the two-photon-driven system. We start from the first-order hamiltonian in the basis |±〉,

Here, in comparison with , the terms associated with the fluctuator are not included () because the important features are contained in the driven qubit–resonator system. In addition, we focus on the two-photon resonance condition ωr=ωq=2ω. Thus, the driving angular frequency ω is largely detuned from ωr and the corresponding term in can be neglected (η=0). Next, we transform the qubit into its energy eigenframe and move to the interaction picture with respect to qubit and resonator, , and . After a rotating-wave approximation, we identify the expression , where the superoperator and its hermitian conjugate . In our experiments, the two-photon driving of the qubit is weak, that is, the large-detuning condition ωq−ω=ω≫(Ω/2)sinθ is fulfilled. In such a situation, it can be shown that the Dyson series for the evolution operator associated with the time-dependent hamiltonian can be rewritten in an exponential form , where

Here, δ≡ωq−ωr is the qubit–resonator detuning. In equation (2), the dispersive shift is a reminiscence of the full second-order component of the interaction hamiltonian, . The terms proportional to are neglected implicitly by a rotating-wave approximation when deriving the effective hamiltonian of equation (2). In this equation, the term renormalizes the qubit transition frequency, and, in the vicinity of the anticrossing (, ), the hamiltonian of equation (1) can be considered equivalent to . In this situation, the symmetries of the system are broken and our experiments demonstrate the existence of real level transitions.

Selection rules

The potential of the three-Josephson-junction flux qubit can be reduced to a one-dimensional double well with respect to the phase variable (ref 20). At the optimal point (Φx=1.5Φ0), this potential is a symmetric function of . For our experimental parameters, we can assume an effective two-level system. The two lowest energy eigenstates |g〉 and |e〉 are, respectively, symmetric and antisymmetric superpositions of |+〉 and |−〉. Thus, |g〉 has even parity and |e〉 is odd. In this situation, the parity operator can be defined via the relations and . The hamiltonian of the classically driven qubit is . For a one-photon driving, ω=Δ/ℏ (energy conservation), the hamiltonian in the interaction picture is , where . This is an odd-parity operator because the anticommutator and, consequently, one-photon transitions are allowed. For a two-photon driving, ω=Δ/2ℏ (energy conservation), the effective interaction hamiltonian becomes , where . As the commutator , this is an even-parity operator and two-photon transitions are forbidden29. These selection rules are analogous to those governing electric dipole transitions in quantum optics. On the contrary, in circuit QED the qubit can be biased away from some optimal point. In this case, the symmetry is broken in a controlled way and the discussed selection rules do not hold. Instead, we find the finite transition matrix elements (Ω/4)sinθ and (Ω2/4Δ)sin2θcosθ for the one- and two-photon process respectively. Beyond the two-level approximation, the selection rules for a flux qubit at the optimal point are best understood by the observation that the double-well potential is symmetric there (Fig. 1d). Hence, the interaction operator of the one-photon driving is odd with respect to the phase variable of the qubit potential20,21, whereas the one of the two-photon driving is even. Away from the optimal point (Φx≠1.5Φ0), the qubit potential has no well-defined symmetry and no selection rules apply.

Spurious fluctuators

The presence of spurious fluctuators in qubits based on Josephson junctions has already been reported previously23. In principle, such fluctuators can be either resonators or two-level systems. As our experimental data does not enable us to distinguish between these two cases, for simplicity, we assume a two-level system in the simulations. In the numerical fit shown in Fig. 2a, we choose owing to the limited experimental resolution. Consequently, the coupling constant estimated from the undriven fit is not , but . Away from the qubit optimal point, especially near the qubit–resonator anticrossings, the effect of the observed fluctuator can be neglected within the scope of this study. Near the optimal point, its effect on the symmetry properties of the system can be explained following similar arguments as given above for the flux qubit. However, it is important to note that, differently from sinθ and cosθ, the fluctuator parameters and are constants, that is, they do not depend on the quasi-static flux bias Φx.

Harmonicity of the L C resonator

We now show that our L C resonator is harmonic and is not populated directly by two-photon driving. Anharmonicities only arise for strong driving, when the maximum induced current density Jmax in the L C resonator approaches the critical current density of the aluminium lines30, Jc≃107 A cm−2. From qubit Rabi oscillation measurements (data not shown), we determine the antenna current Ia≲1 μA resulting in a maximum resonator current Imax=MarIa/Lr≃25 nA. Here, Lr≃200 pH is the resonator self-inductance and Mar≃5 pH is the resonator–antenna mutual inductance. Assuming that the supercurrent flows only within the London penetration depth λL=50 nm, we obtain Jmax≃2.5×102 A cm−2 for our 100-nm-thick film. As Jmax/Jc<10−4, anharmonicities can be neglected safely. Indeed, in the spectroscopy data of Fig. 2b, we observe a pronounced flux-independent one-photon excitation signal of the resonator. On the contrary, two-photon excitation peaks exclusively occur when the qubit is two-photon driven. In other words, the data unambiguously shows that there is no direct two-photon excitation of our resonator.