Main

Researchers in many disciplines use linear regression models widely. The R2 statistic, the coefficient of determination, is one of the most frequently used measures of prediction power and goodness-of-fit for simple linear regression models (Draper and Smith, 1981; Everitt, 2002). In the literature on genetics, researchers often report R2 values of newly identified genetic loci in addition to effect sizes and P-values (Lettre et al., 2008; Weedon et al., 2008). For nonstandard linear regression models, however, several competing R2-like statistics have been proposed to measure prediction power and goodness-of-fit (Buse, 1973; Magee, 1990; Xu, 2003; Kramer, 2005) but have not been used in genetics. Indeed, it is desirable to have a measure for general linear mixed models analogous in some ways to the R2 of the linear regression model, which has a ‘variation explained’ interpretation.

Association mapping searches the association between genetic markers and complex traits (for example disease susceptibility) based on populations (Hirschhorn and Daly, 2005). It complements linkage analysis in mapping the genetic basis of complex traits. Mixed models have long been used in genetic research (Henderson, 1984; Lynch and Walsh, 1998), and the mixed-model association mapping methods were developed to account for complex population structure (Meuwissen et al., 2002; Yu et al., 2006; Malosetti et al., 2007). Although statistics like deviance and the Bayesian Information Criterion (BIC) (Schwarz, 1978) can be used to select models (Broman and Speed, 2002; Littell et al., 2006), many researchers desire a R2-like statistic for mixed models because it can indicate the prediction power of various models containing different fixed and random effects and their associated variance–covariance structure. After identifying statistically significant genetic loci (Kennedy et al., 1992), many geneticists would ask how much of the phenotypic variation is explained by each quantitative trait locus (QTL) for the interpretation or comparison purpose. In other words, what is the relative degree of improvement of the model fit to the data that results by including this significant genetic effect. Moreover, R2-like statistics complement statistical testing by providing practitioners with a more intuitive measurement than the P-value from other statistical tests (for example, likelihood-ratio (LR) test or F-test). Compared with statistics like deviance and BIC, R2-like statistics offer an alternative, easier to grasp measurement for geneticists.

Several approaches can quantify the genetic relationship of a complex population in the context of association mapping using molecular marker information (Weir et al., 2006). The first approach was developed to examine population structure by estimating the probability of subgroup membership (Pritchard et al., 2000; Falush et al., 2003). Recent research showed that principal component analysis (PCA) can also capture population differentiation (Price et al., 2006). A second approach focuses on the pairwise genetic relationship by estimating relative kinship (Loiselle et al., 1995; Ritland, 1996; Yu et al., 2006). As these two approaches are not orthogonal and the same marker data can be used to reflect population structure, principal components, and relative kinship, dependency among these different estimates is expected. Simultaneously fitting these estimates in the model, however, does not necessarily preclude the objective of controlling multiple levels of genetic relatedness within the association panel. In practice, the effects of controlling complex population structure with different estimates (population structure, principal components, and relative kinship) can vary by populations, traits, or both (Yu et al., 2006, 2009; Zhao et al., 2007; Zhu and Yu, 2009). A legitimate question, then, is whether a statistic like R2 can be used to compare the different levels of control for genetic relationships.

Much of the literature on using R2 for nonstandard linear models comes from statistics and econometrics, whereas such literature in the field of genetics is limited. Accordingly, our objectives were to assess the performance of several R2-like statistics for a linear mixed model in association mapping and to identify a general R2-like statistic that measures model-data agreement and provides an intuitive indication of the QTL effect. Although theoretical derivation or developing new statistics are beyond the scope of this study, we introduce four R2-like statistics for nonstandard linear models, describe mixed-model association mapping, and test the performance of these four R2-like statistics in the context of association mapping with computer simulations. We then apply these statistics to two empirical data sets.

Materials and methods

R2 for fixed linear models

For the linear model with only fixed effects

where y is an n × 1 vector, X is an n × k matrix, β is a k × 1 vector of unknown regression coefficients, and e is an n × 1 vector consisting of i.i.d. normal variables with mean 0 and variance σ2. Then the usual R2 statistic is defined as

where . As 0⩽SSE⩽SSTO, it follows that 0⩽R2⩽1.

R2 statistics for linear mixed models

The linear model with both fixed effects and random effects is

where y is an n × 1 observation vector, X is an n × k design matrix linked to the fixed effect, β is a k × 1 vector of unknown regression coefficients of fixed effects, Z is an n × p design matrix linked to the random effects, u is a p × 1 vector of random variables from a multivariate normal distribution (MVN) with zero means and variance–covariance matrix G (that is u∼MVN (0, G)), and e is an n × 1 vector of random errors with zero means and variance–covariance matrix Iσ2 (that is e∼MVN (0, Iσ2)). Thus, y is MVN (Xβ, V) and V=ZGZ′+Iσ2. Several statistics have been proposed for mixed models (Table 1), and we describe them briefly in the following sections.

Table 1 Summary of different R2 statistics for the linear mixed model
Full size table

Two research groups (Cox and Snell, 1989; Magee, 1990) have independently proposed the likelihood-ratio-based R2 (RLR2), a R2-like statistic based on the LR:

where logLM is the maximum log-likelihood of the model of interest, logL0 is the maximum log-likelihood of the intercept-only model, n is the number of observations, and

Please note that the calculation is based on maximum likelihood (ML), not restricted ML (REML). The same formula of RLR2 was also suggested for the binary response models earlier by Maddala (1983). The LR statistic can be written as LR=2log(LM/L0). The relationship between RLR2 and LR is RLR2=1−exp(−LR/n). The RLR2 statistic is appropriate when the concept of residual variance cannot be easily defined and ML is the criterion of fitting the model of interest. It can be shown that when the model only has fixed effects, RLR2 is reduced to the traditional R2 statistic. For discrete models like logistic regression, a scaling procedure should be applied to ensure the resulting RLR2 is bounded between 0 and 1 (Nagelkerke, 1991).

The generalized least square R2 statistic, RW2 is defined as (Buse, 1973):

where is the best predictor of y, and is the weighted mean: with ξ′=(1,…,1). This original definition is denoted as RW12. It can be shown that, with , there is a direct summation relationship:

Replacing with ŷ=Xβ̂+Zû in RW2 yields the RW22 statistic, (Kramer, 2005). There is no direct summation relationship for components in RW22. In addition, it is difficult to interpret the numerator term where V−1, rather than (Iσ2)−1, is used because the random term appears in both (y−ŷ)=(y−(Xβ̂+Zû)) and V=ZGZ′+Iσ2. Here is marginal because the prediction only involves fixed effects, but is conditional because the prediction is conditional on random effects (Vonesh et al., 1996; Vonesh and Chinchilli, 1997; Littell et al., 2006). Note that when the model has only fixed effects, both forms of RW2 are reduced to the traditional R2 statistic.

The rc statistic is a goodness-of-fit measure originally derived for the generalized nonlinear mixed-effect model, following the unweighted concordance correlation coefficient (ρc) (Vonesh et al., 1996):

where n is the number of observations, ȳ is the mean of y, ŷ=Xβ̂+Zû, and ỹ is the mean of ŷ. With ŷ=Xβ̂+Zû, both fixed and random effects are used to measure goodness-of-fit and prediction power and rc is conditional (Vonesh et al., 1996; Vonesh and Chinchilli, 1997). The rc statistic can be interpreted as a measure of the degree of agreement between the observed values and the predicted values as ρc measures agreement between two random variables. The possible values of rc lie in the range −1⩽rc⩽1.

The Prand statistic measures the proportional reduction in the penalized quasi-likelihood function assuming MVN random effects (Zheng, 2000):

where PQLM denotes a penalized quasi-likelihood function for the model of interest, PQL0 denotes a penalized quasi-likelihood function for the null model where the model contains only the intercept, û is the estimated best linear unbiased predictor of u, ŷ=Xβ̂+Zû is the estimated best linear unbiased predictor of y, Ĝ is the ML estimate of G (the variance covariance matrix of u), and ς̂ is the ML estimate of σ. The range of the statistic Prand is 0–1 under these model assumptions. The larger the Prand the better the prediction and the smaller the random effect. The penalty for random effects in Prand is analogous to Akaike’s Information Criterion and Schwarz’s BIC. Note that when the model has only fixed effects, Prand is reduced to the traditional R2 statistic.

Models in association mapping

When both population structure (Q) and kinship (K) are included, the mixed model for the Q+K method is

where y is a vector of phenotype observation, μ is a vector of intercepts; v is a k × 1 vector of population effects; u is a p × 1 vector of random polygene background effects; e is a vector of random experimental errors; Q is an n × k matrix defining the subgroup membership, generated from population structure analysis of marker data, and Z is an n × p incidence matrix relating y to u. For Var(u)=G=2KVg, K is a p × p matrix of kinship coefficients, and Vg (a scalar) is the unknown genetic variance, E(e)=0 and Var(e)=Iσ2.

Likewise, we can define the Q model without the Zu term; the K model without the Qv term; the P model with P (that is eigenvectors) from PCA replacing Q but no Zu term; and the P+K model with P replacing Q (Table 2). These models represent different combinations of methods that account for complex genetic relationships in the association mapping population (Yu et al., 2006; Weber et al., 2007; Zhao et al., 2007).

Table 2 Models used in the data analysis
Full size table

Computer simulation

To assess the performance of these R2 statistics in the context of mixed-model association mapping, we generated genetic populations with both gross level population structure and familial relationships within subpopulations. This allowed us to investigate mixed models with both fixed effects for population structure and random effects for relative kinship. Detailed simulation procedures have been described earlier (Zhu and Yu, 2009). Briefly, the β distribution (Balding and Nichols, 1995; Nicholson et al., 2002; Marchini et al., 2004) was used to model the correlated allele frequencies. Once allele frequencies of each locus for each subpopulation were sampled under the β model, conditionally on Hardy–Weinberg and linkage equilibrium, we mimicked different populations consisting of subpopulations. Specifically, we carried out simulations that mimicked two types of population used in association studies (Yu et al., 2006; Zhu and Yu, 2009): samples with both population structure and familial relatedness (type IV) and samples with severe population structure and familial relationship (type V). As with earlier extensive simulations (Zhu and Yu, 2009), the population size was 216, and three subpopulations were simulated for type IV and V samples. For each sample type, a total of 500 independent data sets were generated for analysis with three different models, and the various R2 statistics were obtained. Samples in which the Hessian matrix or the covariance matrix of the random effects (seven for type IV and four for type V) were not positive semidefinite were removed.

To generate genotypes and phenotypes, a linkage map of 2000 cM composed of 10 chromosome segments, each 200 cM in length, was considered. An additive genetic model with no dominance or epistasis was used. Of the 2000 single nucleotide polymorphism (SNP) locations, 25 were chosen at random to be quantitative trait nucleotide (QTN) locations. In all simulations, we set each QTN genotypic value with genotype QQ as 0.5, genotype qq as 0, and the overall mean at 10. The overall genotypic value of an individual was obtained as the sum of genotypic values across all QTN plus the overall mean. An individual phenotype was generated as the genotypic value plus a random variable sampled from a standard normal distribution. Heritability for each QTN varied around 2%, depending on the allele frequency at each specific QTN.

To verify the general agreement between the RLR2 statistic and the detection of true QTNs, we plotted the values of RLR2 for all SNPs with the P+K model from a random run of type IV samples.

Empirical data analysis

Data from two association mapping populations were used for empirical data analysis. Genotypes and three phenotypes (that is flowering time, ear height, and ear diameter) were chosen from 277 maize strains across 553 SNP as described earlier (Liu et al., 2003; Flint-Garcia et al., 2005; Yu et al., 2006). The Q matrix was computed by STRUCTURE (Pritchard et al., 2000; Falush et al., 2003) and the K matrix by SPAGeDi (Hardy and Vekemans, 2002). The P matrix was computed from EIGENSTRAT (Price et al., 2006), and three PCAs were used to be consistent with the Q matrix for degree of freedom in the model-fitting process. Arabidopsis genotypes and phenotypes were obtained from a published data set with 5419 SNPs and two flowering time measurements (SDV and JIC8W) (Zhao et al., 2007). These two traits passed our trait screening process and yielded meaningful variance component estimates for mixed-model analysis. The Q matrix contains eight subgroups, and the P matrix contains the first eight PCAs (Zhao et al., 2007). For RLR2, we modified the Venn diagrams to depict the overlapping but complementary nature of Q and K in capturing genetic relationships. The modification was to make the size of the circle proportional to the RLR2 value for easier interpretation of the diagram.

Results

All R2 statistics (Table 1) yielded values between zero and one when different models were used to analyze data from two association mapping sample types, except the RW12 statistic (Table 3). Notably, the zero values for RW12 under the K model were not unexpected because its definition excludes random effects in calculating the predicted value. However, including the random term in prediction (RW22) yields values comparable to those of other R2 statistics.

Table 3 Performance of R2 statistics from different models under two association sample types
Full size table

When only the fixed effect was involved (that is P model), four R2 statistics (that is RLR2, RW12, RW22, and Prand) yielded identical values (Table 3). This was expected because theoretical derivation showed that all three definitions reduce to the original R2 form for the fixed linear model. Meanwhile, the rc statistic yielded different values for the fixed-effect model P because its formula does not reduce to R2 for the fixed linear model.

Comparing an R2 statistic among P, K, and P+K models showed differences between having a variable missing and having it added. Notably, RLR2 for the model with added variables (P+K model) was consistently higher than for the model with fewer variables (P or K model) without exception, but this was not the case for other R2 statistics (Table 3). Moreover, the standard deviation of RLR2 was either equal to or smaller than that of other R2 statistics. Also, the range of R2 statistics was 0–1 except when the Hessian matrix or the covariance matrix of the random effects was not positive semidefinite, with the resulting negative value for Prand removed in calculating the mean and standard deviation.

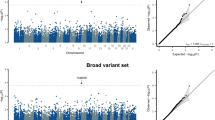
After determining the suitable candidate R2 statistic for model comparison in mixed-model association mapping, we further demonstrated changes in RLR2 as the QTNs and other SNPs across the genome entered the mixed model individually (Figure 1). To do this, we used a type IV association mapping sample. As expected, RLR2 values with the SNP/QTN term were equal to or greater than the baseline RLR2 value from the model without the SNP/QTN term. As the variation due to individual QTNs varied depending on allele frequency, not all QTNs yielded a high RLR2 when their effects were included in the model. On the other hand, some SNPs can show a high RLR2 even when they were not the causal loci, revealing the challenges faced in association mapping.

Figure 1
figure 1

The RLR2 values of the mixed model including each SNP across the genome. Triangles indicate the RLR2 values and positions of the QTNs simulated and the straight line under the curve is the baseline RLR2 value of the mixed model without SNP. Note that the way the computer simulation was carried out does not allow all QTNs to have a high RLR2 value, mimicking the complex scenarios that are typical in association mapping studies.

Full size image

For the maize data, only RLR2 consistently yielded a higher value for models with more variables (Q+K or P+K) than models with fewer variables (Q, K, or P) across three traits (Table 4). Next, for models with only fixed effects (that is Q or P), rc values were different from the other four statistics, which agrees with the theoretical expectation and the simulation results. Furthermore, for Arabidopsis data, RLR2, rc, and Prand yielded a higher value for models with more variables, but this was not the case for RW12 or RW22 (Table 5).

Table 4 Analysis results of different R2 statistics obtained by analyzing the maize traits with different models
Full size table
Table 5 Analysis results of different R2 statistics obtained by analyzing the Arabidopsi s traits with different models
Full size table

In the modified Venn diagram, RLR2 shows the overlap between the two methods in accounting for genetic relationships: population structure (Q) captures general grouping patterns and relative kinship (K) is a polygene background control (Figure 2). The relative importance of Q and K in model fitting varied for different quantitative traits, which was expected given the theory (Tables 4 and 5). The complementary nature of P and K can also be seen in the modified Venn diagram. Obviously, the relative contribution of Q, P, and K to the mixed-model analysis varied across different data sets or different traits. For example, both Q and P made a small contribution in the analysis of maize ear diameter, but including K only improved the model fit by a negligible amount, as shown by a small increase in RLR2.

Figure 2
figure 2

Modified Venn diagrams for RLR2 values from different models obtained for (a) maize and (b) Arabidopsis traits. The number in each circle is the RLR2 value of either the Q or K model, the RLR2 value of the Q+K model is given under the jointed circles, and the number in the jointed area indicates the overlap between two complementary methods (i.e., Q and K) in controlling genetic relationship.

Full size image

Discussion

Various R2-like statistics for mixed models revealed the mixed perspectives on how the goodness-of-fit of the mixed models should be measured. For instance, the RLR2 statistic, based on the LR test (Magee, 1990), considers the change of likelihood between models with different fixed and random effects simultaneously. However, the RW2 statistic, based on the Wald statistic (Buse, 1973), measures the agreement between observations and the generalized least square predictors without considering random effects. The modified form, RW22, which considers both random and fixed effects, would be a better choice than RW12 for analyzing genetic relationships but needs further study. Next, the rc statistic, based on the concordance correlation (Vonesh et al., 1996), indicates agreement between observations and the unweighted predicted values with both fixed and random effects, whereas the Prand statistic, based on the penalized quasi-likelihood function (Zheng, 2000), measures the proportional reduction in penalized quasi-likelihood function. When only fixed effects are included in the model, three R2 statistics, but not rc, reduce to the simple form for fixed linear models. By definition, all R2 statistics other than RW12 would be suitable for genomic mapping with different fixed and random terms controlling genetic relationships. The zero value of RW12 for the K model prevents its use in mixed-model association analysis. In comparing RLR2 and RW22 for mixed-model analysis of a randomized complete block design and a design with spatially autocorrelated residuals (Kramer, 2005), the R2 values of these two statistics increased when random effects were added to the model or when the correlated error structure was considered.

As the direct summation of sum of square of model and sum of square of residual to equal sum of square of the corrected total does not necessarily exist in generalized linear mixed models, the term ‘Pseudo-R2’ was suggested to differentiate the above proposed statistics from the classical R2 (Schabenberger and Pierce, 2002). We, however, adopted the general definition of the R2 statistic (Buse, 1973; Magee, 1990; Nagelkerke, 1991), rather than the specific definition for a fixed linear model, in the text. Here, we stress that the ‘proportion of variation explained’ in linear mixed models should not be interpreted to mean that there is always an exact summation. In this study, we focused on comparing four different R2 statistics for their potential in mixed-model association mapping. All these statistics contain similar components, involving differences between the observed values and the predicted values (either directly in RW2, rc and Prand or indirectly in RLR2). In particular, the RLR2 statistic has several appealing properties (Nagelkerke, 1991). First, it reduces to the classical R2 for fixed models and is asymptotically independent of the sample size. Second, it is dimensionless and permits an interpretation based on proportion of variation explained. Furthermore, using RLR2, to compare models with the same random components (that is K with Q+K or P+K) can be interpreted as comparing the fit of various nested models. On the other hand, comparing models with different fixed and random components provides a measure of model-data agreement under the ML framework, which satisfies a criterion proposed earlier: R2 values for different models fitting the same data should be directly comparable (Kvalseth, 1985).

Ultimately, because it is easily computed and its monotonic nondecreasing property, RLR2 is our choice to measure the goodness-of-fit of the model to the data. Expanding the mixed model to include other genetic and nongenetic factors should not complicate the calculation and interpretation of RLR2 because it is directly computed from the maximum log-likelihood of the full model and the reduced model. In simulation studies, an R2 measure computed as the squared correlation between simulated and model predicted genetic values may be used (Piepho and Möhring, 2007). Other R2 statistics based on the ratio of variance component for residuals between two models have also been proposed (Xu, 2003). A recent study, however, found that these latter statistics performed poorly because the R2 values varied so little that identifying the most parsimonious model was difficult (Oreliena and Edwards, 2008). Extending RLR2 to the REML approach needs further study because comparing models with different fixed or random terms is only valid under the ML framework (Littell et al., 2006). The relationship between model fit and model selection, particularly in genomic mapping, is beyond the scope of this study (Broman and Speed, 2002; Sillanpaa and Corander, 2002; Yi et al., 2005). We have no intention of using RLR2 to conduct model selection because the monotonic nondecreasing property of RLR2 does not indicate a better model as additional fixed or random effects are added. Instead, we stress that the RLR2 statistic provides an additional measurement for results interpretation.

For mixed models with random components (K, P+K, or Q+K), variance component estimation was conducted independently before the solutions for mixed models were used to compute different R2 statistics. On the basis of the definition of RLR2, the convergence process of ML of a model containing additional effects other than intercept and residual can also be viewed as a process to maximize RLR2 but not the other R2 statistics. Clearly, RLR2 can quantify the goodness-of-fit of different models regardless of the statistical properties of the models (Cameron and Windmeijer, 1996). In an earlier study, we showed that the likelihood-based model-fitting approach can quantify the robustness of genetic relationships derived from molecular marker data (Yu et al., 2009). Essentially, kinship construction with subsets of the whole marker panel and subsequent model testing with multiple phenotypic traits can be viewed as a process to test the model-data fit of different variance–covariance matrices. With an adequate number of molecular markers, an accurate genetic relationship among individuals (that is variance covariance matrices) can be obtained, and the change in the value of RLR2 becomes minimal.

Comparing the values of RLR2 for Q, K, and Q+K, as shown with modified Venn diagrams, can help us understand the genetics behind two overlapping methods in accounting for genetic relationships. With complex genetic relationships among individuals in many association mapping panels (Meuwissen et al., 2002; Yu et al., 2006; Zhao et al., 2007; Zhu and Yu, 2009), various competing but mostly complementary methods to capture these relationships were developed. Thus, the contribution to the model-data agreement from either Q and P (population structure and PCA) or K (kinship) can be determined from the RLR2 when each is fitted alone. Next, the overall contribution and overlap can be shown by comparing the RLR2 values of Q+K (or P+K) with the values from models with individual components (that is Q, P, or K). Finally, although it is not a statistic with a significance test, RLR2 does provide an indication of a variable's importance in model fitting, for example, SNP, Q, P, or K (Kvalseth, 1985). With an established base model (Yu et al., 2006), the changes in RLR2 values resulted from adding individual molecular marker provide information on the relative importance of different markers in further explaining the total variation.

In summary, we demonstrated through simulated association mapping samples and empirical data analyses that the LR-based R2 statistic has several desirable properties useful in mixed-model association mapping. Applying genomic technologies in complex trait dissection has generated vast amounts of data, the analysis of which requires a joint effort in genetics and statistics. There are many challenges in this multidisciplinary research (Hirschhorn and Daly, 2005; Weir et al., 2006; McCarthy et al., 2008; Zhu et al., 2008), but such research also provides great opportunities for further collaboration among researchers from different disciplines with different specialties.