Introduction

Statistical analysis for testing simultaneously a large number of hypotheses in genome-wide association studies (GWAS) has received considerable attention. Several algorithms have focused on two- or multi-stage procedures, or on the selection of ordered P-values under a controlled error rate.1, 2, 3 Other procedures have suggested a mixture structure on P-values, or have adopted the null normal distribution with a dispersed density such as a mixture of beta distributions or a mixture of normals.4, 5 The underlying principle of all these methods is to separate the markers into two groups on the basis of P-values, one showing association with the disease trait and the other not. It is thus intuitive to incorporate the mixture approach in genomic analysis, in which only a small proportion, say λ, among the enormous number of markers shows association. Our rationale for using a mixture model, however, goes beyond the purpose of clustering, as it considers the estimation procedure primarily as a tool of inference and it accommodates the possible dependence among markers directly.

An estimation approach, rather than hypothesis testing, has earlier been advocated for large-scale association studies primarily so as to avoid overinterpretation of statistical significance.6 By adopting the mixture model, we get an important advantage of incorporation of dependence among observed data, when several sources of dependence arise. For example, linkage disequilibrium (LD) among dense SNPs is one source of correlation. Genotyping data collected from a given individual may produce within-subject dependence. Markers associating with the disease phenotype share the common feature of ‘showing association,’ and thus may induce yet another type of correlation within a gene set or pathway. Whereas the existence of such dependence in data, and thus among the statistics, may complicate the task of multiple hypotheses testing, a mixture structure on a properly defined statistic may in contrast provide an explanation of dependence in general. For these reasons, several GWAS have adopted the mixture model conceptualization.4, 7

Bayesian statistical inference has attracted many researchers for its ability to deal with complex models and with uncertainty from different sources.8 For example, an exploration approach and an empirical Bayes approach with hierarchical modeling have been considered.9, 10, 11 Others have proposed a fully Bayesian approach with a Dirichlet process mixture model for differential gene expression, or a hierarchical mixture model for normalized microarray data.12 These models are useful when the information about an evolutionary region or linkage is available, though they may be computationally intensive because of a large number of parameters. Other proposals have included use of an asymptotic Bayes factor (BF) as a means of incorporating the information of minor allele frequency (MAF) and sample size,13 and using a hierarchical mixture model on the logarithm of odds ratios as was briefly mentioned earlier.14 Nevertheless, a specific mixture distribution accommodating different sample sizes and variances among various markers has not been previously suggested.14 The large number of parameters remains a challenging task. Other proposals have included the false positive report probability, a combined measure of frequentist significance and Bayesian subjective probability.15 Criticism arises, however, with its Bayesian interpretation.16 Therefore, for GWAS, a fully Bayesian approach with a simpler model may provide a better tool for inference and for wider applicability.

We propose here a hybrid procedure based on a Bayesian hierarchical mixture model for biallelic markers. This Bayesian mixture model considers not only the grouping of markers, but also the general dependence among data. This model is able to capture the existing dependence with only a few parameters, and thus is simpler than other Bayesian models. There are two important features of our proposed model of particular note. First, we consider a statistic yi, standardized to be of unit variance, and use a mixture structure on its parameter γi. In other words, this yi represents the ‘standardized’ difference in allele frequencies between case and control groups, and is drawn from a distribution with a mean √ni × γi and variance 1, where ni is the sample size and the index i ranges from 1 to M markers. The use of such yi has a major function in our procedure and its contribution will be explained in later sections. The mixture prior on γi is an important element to account for the general dependence among statistics. In contrast to other mixture structures on P-values or on their transformations, such as test statistics, the adopted model is more intuitive and simpler to implement. Second, the information contained in the mean parameter γi is not affected by the sample size. Without worrying about the influence from the sample size, a unit information prior for the i-th marker becomes easier to formulate. In addition, most procedures consider the small proportion of association markers, λ, a nuisance parameter and often fail to provide a stable estimate for it, not to mention failing to use its estimate at the stage of selecting significant components. We will show here that the posterior inference of λ improves greatly the performance of the association test. After estimation of λ, a test with the BF at the marker-specific level is carried out to rank and identify susceptible genes.17 Several GWAS from the Wellcome Trust Case–Control Consortium (WTCCC) as well as simulations are used to evaluate performance of the model.

Materials and methods

Bayesian mixture structure

Suppose there are M markers under study, and let λ denote the small proportion of association markers among them. The mixture setting of M × λ and M × (1−λ) markers within a Bayesian hierarchical model then explains the dependence among markers through their corresponding ‘standardized’ statistics yi's as follows. For the i-th marker, yi is the standardized difference in genetic measurements, say gene expression levels, between two types of tissues or experimental conditions:

where ĝcs,i and ĝcn,i are the observed average levels for the case group and for the control group, respectively; ncs and ncn are the numbers of tissues in each group; and ς̂2cs and ς̂2cn are estimates of variance in each group.

Each yi is of unit variance and represents a standardized effect size. For biallelic markers such as SNPs, yi is the ‘standardized’ difference in allele frequencies between two groups,

where p̂cs,i and p̂cn,i are the observed minor allele frequencies (MAFs) of the i-th marker for the case and control groups, respectively. Note that for biallelic markers, this standardization uses the empirical variance estimates without loss of degrees of freedom in estimation. Therefore, this procedure is able to avoid the formulation of a prior distribution on nuisance variance parameters. This model is more flexible than one that assumes equal variance for all markers,9 and is easier to work with than a highly parameterized model with unequal variances for all markers.

To satisfy the purpose of association studies, we specify the mixture structure on the mean standardized risk difference γi. For ease of notation, let ni=ncs,i=ncn,i; then the mean of yi can be factored as γi × √ni, where γi is a function of the MAFs. This γi follows a mixture distribution with a mixing parameter λ,

That is, with probability 1−λ, γi follows a distribution f0 of no association, whereas with probability λ, γi follows f1, a uniform distribution over (−u,−t) and (t,u) of association. The mixing weight (1−λ) denotes the majority of non-associated markers, and f0(γi) can be a conservative indicator function, I(0), degenerating at the zero mass, or a distribution over a pre-specified interval for ‘no association.’ Under f1, γi ranges in the set (−u,−t)∪(t,u) (see Supplementary Materials for discussion about their values and the complete model specification).

Effect size and rare MAF

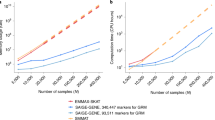
The standardized risk difference γi here can be considered as a measure of effect size. As compared with the odds ratios, it is much less sensitive to rare MAFs. The influence from rare MAFs is reduced to a minimum because yi has been standardized by its SD. In Figure 1a and b, the solid lines show the behavior of γi and the odds ratio, respectively, versus the rare MAFs of the control group. It is apparent that γi remains stable in the range of rare MAFs, while the odds ratio, even divided by 10 (OR/10), contains much more variation. The same pattern can be observed when the difference in allele frequencies between two groups is fixed (dashed lines in Figure 1). Therefore, a mixture structure on γi is more suitable in terms of variability than an odds ratio.

Figure 1
figure 1

The solid lines are values of (a) γi (OR/10 in (b)) versus pcn (small MAFs of the control group) at different fixed values of pcs. The dashed lines are values of (a)γi (OR/10 in (b)) versus pcn at fixed values of pcs−pcn (pcs−pcn=0.02, 0.01, and 0 from top to bottom, respectively).

Full size image

Formulation of the priors

For the two components f0 and f1 in the mixture distribution of γi, we consider an indicator function for f0(γi) and a uniform distribution for f1. The latter implies that all values are equally likely over the intervals (t,u) and (−u,−t). When the case and control groups are of the same size (ie, ncs=ncn), the range can be derived analytically as (t=0.071, u=0.825) for biallelic markers with MAFs in (0.05, 0.50). When sample size differs, the range depends on the ratio of ncs and ncn (see Supplementary Material). The above finite values are recommended from a conservative viewpoint, because a larger u would imply stronger evidence against the null a priori, and may lead to an improper posterior for inference.

Hybrid method of the global estimate and the BF

With the likelihood, mixture structure, and prior distribution established, the posterior distribution of λ can then be derived (Supplementary Material). Next, based on this posterior distribution f(λ∣y1,…,yM), one can estimate λ, the proportion of influential markers, and proceed to the statistical inference. We term the estimated posterior mode, , the global estimate of the association proportion. In other words, M × is the estimated posterior mode of M × λ, the number of association markers. This estimate borrows strength from all marker information, and, as the results will show later, it is accurate and stable. If the estimated proportion is non-zero, then a total of M × markers are considered candidates and will be selected by the rankings of the BFs17 for the M markers. The smaller the BF, the stronger the evidence supporting the association with the disease under study.

To compute the BF for the i-th marker, we test λi=0 indicating no association versus λi=1 indicating an association. Next, we select the leading M × markers with the largest values of 1/BF, the inverse of BF. The magnitude indeed implies directly the strength of evidence for association.17 In general, when BF is less than 1/100, the strength of evidence against the null is considered decisive;17 that is, the data provide strong evidence supporting the association. Using the threshold 1/100 for BF usually results in more signals than using the global estimate, and is considered more conservative.

Results

WTCCC association studies

We consider genotyping data from the WTCCC18 to evaluate the performance of the hybrid Bayesian procedure and to compare it with other existing methods. From the WTCCC archive, we obtained genotyping data originally from 1999 rheumatoid arthritis (RA) patients, 1988 patients with coronary artery disease (CAD), 2004 with Crohn's disease (CD), and 3004 common controls. Exclusion criteria for SNPs were (1) MAF <0.05, (2) call rate <95%, and (3) failure to meet the quality control criteria of the WTCCC.18

Rheumatoid arthritis

After passing the quality control filters of the WTCCC, a total of 366 037 SNPs were selected for 1860 RA patients and 2938 controls for our analysis. Earlier studies have established an association region, the major histocompatibility complex, also called the HLA complex, on 6p21, and a gene PTPN22 on 1p13.2.17, 18, 19, 20, 21 Here, we examine whether these findings can be replicated by the proposed method.

Table 1 lists the estimated number of association markers based on the Bayesian hybrid procedure (Bayes), the Bonferroni procedure (Bon), q-values, the Benjamini and Hochberg procedure (BH), and a false discovery control with a P-value weighting scheme (wBH).22 Among the 232 SNPs identified by the Bayesian procedure, 9 are near PTPN22 on 1p13.2, and 200 are in 6p21.32–6p21.33. Both regions generated strong signals. In fact, 217 of the SNPs are on either chromosome 1 or 6. For comparison, the number of SNPs identified by all other procedures (except Bon) is >1.5 times the number (232) obtained with our procedure, and may result in more false positive regions, while the Bon provides the smallest number 200. Figure 2a displays the distributions of these 232 SNPs, and Figure 2b shows the Manhattan plot of the negative log10 transformation of BFs. Supplementary Table A.1 lists their chromosome locations. For those SNPs whose individual BFs imply decisive evidence, details are in Supplementary Table A.2. The Bayesian inference further provides a measure of association strength for each marker (ie, BF< 1/100). The identified SNPs merit further functional or pathway analysis, and can serve as the next candidate regions for further analysis (Supplementary Table A.2).

Table 1 Numbers of influential markers for three studies (RA, CAD, CD) from WTCCC under different methods
Full size table
Figure 2
figure 2

(a) Grey bars represent the numbers of SNPs passing the quality control filters for the corresponding chromosomes. The values at the bottom of the bars indicate the numbers of SNPs selected by for RA. (b) Plot of −log10(BF) by chromosome locations.

Full size image

Coronary artery disease

On the basis of the quality control criteria, a total of 365 984 SNPs of 1926 subjects with CAD were derived. The Bayes identified 26 SNPs, the Bon selected 29 SNPs, and the others 42. Among the 26 SNPs, 16 are in 9p21.3. This region contains two cyclin-dependent kinase inhibitors, CDKN2A and CDKN2B, both of which have been reported to associate with CAD.23 The locations of identified SNPs are displayed in Figure 3 and the details are in Supplementary Table A.1. It is worth noting that, although the earlier identified APOE gene on 19q13 did not show a signal in the WTCCC reports and was not selected by either, the Bayesian test did provide decisive evidence of association (ie, BF<1/100, Supplementary Table A.3). This again shows the advantage of the hybrid procedure in providing candidate markers based on the strength of evidence.

Figure 3
figure 3

(a) Grey bars represent the numbers of SNPs passing the quality control filters for the corresponding chromosomes. The values at the bottom of the bars indicate the numbers of SNPs selected by for CAD. (b) Plot of −log10(BF) by chromosome locations.

Full size image

Crohn's disease

A total of 366 251 SNPs and 1748 subjects with CD passed the quality control filters, and were included in the analysis. Seventy-four SNPs were identified by the Bayesian global estimate, 72 were determined by the Bon, 178 by q-values, and 167 by both BH and wBH. The locations of identified SNPs are presented in Supplementary Figure A.1 with details in Supplementary Table A.1.

Among the identified 74 SNPs, 22 were in 5p13.1, 15 in 1p31.3, 12 in 16q12.1, 7 in 10q24.2, and 5 in 2q37.1, respectively. These regions have all been identified in earlier research as containing genes associated with CD: the gene PTGER4 on 5p13, IL23R on 1p31, NOD2 on 16q12, NKX2-3 on 10q24.2, and ATG16L1 on 2q37.1. Three other SNPs on 5q23.1, 10q21.2, and 18p11.21 were in different regions. For the remaining 10 SNPs, the values of BFs also imply remarkably strong association (Supplementary Table A.4). Further replication studies or pathway analysis would be necessary for confirmation.

Simulation study

Here, we show the performance of this proposed procedure with simulated data, especially with correlated markers. We consider the independent and correlated settings separately with λ between 0.001 and 0.1. The dependence setting uses a spatial structure for correlation for LD, where the correlation between any two markers depends on the physical distance,

where dij is the distance between the i-th and j-th marker, and θ is a pre-specified tolerance distance for correlation. The dij follows a Poisson distribution and θ depends on the maximum correlation in the generated data. The procedures for generation of dij and determination of θ are documented in Supplementary Material. Note that when M is larger than 1000, the correlation between markers at two ends becomes extremely small and thus markers become almost independent. Therefore, it suffices to set M at 1000 in all 100 replications. The global estimation of λ is derived, and other existing methods are also performed for comparison.

The results are displayed in Figure 4 and Supplementary Table A.5. For the point estimate of λ under independent markers, all procedures provide good estimates, except the conservative Bon. However, when data are simulated with the dependence structure, the Bayesian global estimate performs the best (Figure 4b). Its performance is consistently stable and is not affected by the data structure. The corresponding standard error is small as well (<0.1% under the independence model and <1% under the dependence model). The q-value (Storey_q) overestimates to a greater degree, confirming the findings in the WTCCC analysis that it tends to overestimate, whereas BH, wBH, and Bon all underestimate (details in Supplementary Materials). We have carried out other simulation studies with settings such as M=100 000 and λ=0.0001, and the results are as good as the case reported here.

Figure 4
figure 4

Estimated proportion versus true λ for (a) independent and (b) dependent markers. Bmix is the global estimate, Storey_q for q-values, BH for Benjamini and Hochberg procedure, wBH is false discovery control with P-value weighting, and Bon for Bonferroni procedure.

Full size image

Discussion

On the basis of a simple Bayesian hierarchical mixture model, the hybrid procedure we have used in this article to detect susceptible genes for GWAS has proven useful and robust for extremely small λ. The major contributions of our approach are the use of the standardized statistic yi, and a further decomposition of its mean to the product of γi and √ni. This novel design and factorization are essential within this setting as they make inference of the proportion of association feasible with a fewer number of parameters – this is a case different from and not explicitly considered by others.14 The standardized risk difference γi, in addition to the direct interpretation it affords and the easier formulation of priors, is robust to small MAFs and small differences in MAFs, as opposed to when OR or log(OR) is the parameter of interest. The global Bayesian estimate performs well in terms of point accuracy, true positive rate, false positive rate, and proportions of false positive, for both independent and dependent markers (Supplementary Figures A.2–A.4). Furthermore, the second step of the BF evaluation quantifies the strength of evidence for association, and offers a way to measure the ‘importance’ of markers, thereby making possible allocation of appropriate research resources to the different markers. This quantitative comparison is an advantage that the procedures based on P-values cannot provide.

There are several issues meriting discussion with regard to extension of the model. First, the statistic yi illustrated here is based on the standardized difference in allele frequencies. This can be extended to data of genotype counts or microarray data. For instance, for any risk allele under the dominant or recessive model, the difference in frequencies of genotypes under study can be computed and standardized to derive the global estimate. However, one should be cautious in estimating variance. For biallelic markers as discussed here, estimation of the variance does not lose extra degrees of freedom, whereas for other data types, this may not hold true. Second, with microarray data, the range of γi in the reference prior will differ from the values considered for (t,u) in simulations. In our implementations, we suggest the 10th percentile of yi for t. In fact, our investigations show that any other smaller value will not make any difference in the results. As for u, it has to be greater than all yi's, and hence the maximum of yi is recommended. Other larger numbers are certainly allowable. Third, for gene expression profiling data, this procedure can be compared with current procedures such as the maxT test. Fourth, for the prior specification on γi, other choices with informative priors are possible. The analytical derivation of the global estimate should be straightforward, or numerical implementations can be adopted. Finally, as already mentioned, this Bayesian hierarchical model is used here to detect association markers based on the hybrid procedure, particularly when the proportion of influential markers is very small, or when quantification of the degree of association is of interest. Further applications include meta-analysis of various GWAS to measure small effects and to assess the degree of heterogeneity among studies. The need to synthesize results across multiple studies indeed opens the era for methodological research and collaborations among different disciplines.