Abstract
We propose a dressed-state scheme to achieve shortcuts to adiabaticity in atom-cavity quantum electrodynamics for speeding up adiabatic two-atom quantum state transfer and maximum entanglement generation. Compared with stimulated Raman adiabatic passage, the dressed-state scheme greatly shortens the operation time in a non-adiabatic way. By means of some numerical simulations, we determine the parameters which can guarantee the feasibility and efficiency both in theory and experiment. Besides, numerical simulations also show the scheme is robust against the variations in the parameters, atomic spontaneous emissions and the photon leakages from the cavity.
Similar content being viewed by others
Introduction
Quantum state transfer and entanglement generation between different systems with time-dependent interacting fields have become more and more important for the further development of quantum information processing1,2,3. In order to achieve the high-fidelity quantum state transfer and entanglement generation, adiabatic evolution which corresponds to a state transfer along the adiabatic eigenstates is an excellent candidate method4,5. The most widely used approach of adiabatic evolution is stimulated Raman adiabatic passage (STIRAP) because of its great robustness against pulse area and timing errors as well as the restraint on lossy intermediate states.
However, STIRAP schemes usually require a relatively long interaction time, and thus the adiabatic evolution may suffer from dissipation and noise during the process of quantum state transfer. Therefore, it is greatly necessary to speed up the process of adiabatic evolution and lots of theoretical schemes have been brought forward6,7,8,9,10,11,12,13,14,15,16,17,18. Besides, some experimental realizations have been completed19,20,21,22,23. There are two techniques, transitionless quantum driving and Lewis-Riesenfeld invariants, widely applied to speed up adiabatic quantum state transfer and entanglement generation24,25,26,27,28,29,30. Although, in theory, the high-fidelity adiabatic quantum state transfer and entanglement generation can be achieved by transitionless quantum driving and Lewis-Riesenfeld invariants, it is hardly possible in practice due to the major flaws of the two techniques. On one hand, a transitionless-based direct coupling between the initial state and the target state is too hard to be obtained experimentally31,32,33. On the other hand, in some schemes34,35,36,37,38, invariants-based driving pulses are not smoothly turned on or off and thus lead to severe impediments in experiment.
A short time before, Baksic et al. proposed a new method to speed up adiabatic quantum state transfer by using dressed states39. In ref. 39, the dressed states are skillfully defined to incorporate the nonadiabatic processes. Kang et al. used the dressed-state method to implement the entanglement generation in a solid quantum system40. In this work, we apply the dressed-state method to quantum state transfer and entanglement generation between two Λ-type atoms trapped in an optical cavity. With the assist of quantum Zeno dynamics41,42, the original system Hamiltonian is simplified and viewed as a three-level system. With the addition of a suitable correction Hamiltonian to the original Hamiltonian and the ingenious unitary transformation, we construct a new diagonal Hamiltonian in the time-independent dressed-state frame. Then the adiabatic two-atom quantum state transfer and entanglement generation are speeded up in a non-adiabatic way.
Adiabatic quantum state transfer and entanglement generation between two atoms
The schematic setup for quantum state transfer and entanglement generation between two atoms is shown in Fig. 1. Two Λ-type atoms A and B are trapped in a single-mode optical cavity. Each atom has an excited state |2〉 and two ground states |0〉 and |1〉. The atomic transition |2〉A(B) ↔ |1〉A(B) is resonantly coupled to the mode of the cavity with corresponding coupling constant gA(B), and the transition |2〉A(B) ↔ |0〉A(B) is resonantly driven by a classical field with the time-dependent Rabi frequency ΩA(B)(t). Then the atom-cavity system can be dominated by the interaction Hamiltonian (setting ħ = 1)

where Hal(t) (Hac(t)) is the interaction between the atoms and the classical laser fields (the mode of the cavity), and a is the annihilation operator of the cavity mode. For simplicity, we assume gA = gB = g. Then suppose that the total system is initially in the state |ϕ1〉 = |0〉A|1〉B|0〉c denoting atom A, atom B and the cavity mode in the state |0〉A, state |1〉B and vacuum state, respectively. Thus dominated by the Hamiltonian (1), the whole system evolves in the Hilbert space spanned by

Obviously, the system is initially in the dark state of Hac(t), i.e., Hac(t)|ϕ1〉 = 0. Then choosing the quantum Zeno limit condition  , the whole system can approximatively evolve in an invariant Zeno subspace consisting of dark states of Hac(t)43,44
, the whole system can approximatively evolve in an invariant Zeno subspace consisting of dark states of Hac(t)43,44

corresponding to the projections

Here,

Therefore, the system Hamiltonian can be rewritten as the following form45

in which  and
and  . Then the pulses are parameterized by the frequency Ω(t) and the angle θ(t)
. Then the pulses are parameterized by the frequency Ω(t) and the angle θ(t)

with  and θ(t) = arctan(Ω1(t)/Ω2(t)), and we can easily obtain the time-dependent eigenstates of H(t)
and θ(t) = arctan(Ω1(t)/Ω2(t)), and we can easily obtain the time-dependent eigenstates of H(t)

with the eigenvalues Ed = 0 and E± = ±Ω(t), respectively.
Next we move the Hamiltonian (6) to the time-independent adiabatic frame defined by the unitary operator U(t) = ∑j=d,±|φj〉〈φj(t)|, and the Hamiltonian (6) becomes

with Mz = |φ+〉〈φ+| − |φ−〉〈φ−| and  H.c. The second term of the Hamiltonian (9) corresponds to the nonadiabatic couplings which may lead to an imperfect state transfer. In order to correct the nonadiabatic errors, we look for a correction Hamiltonian Hc(t) such that the modified Hamiltonian Hmod(t) = H(t) + Hc(t) governs a perfect state transfer. Here we choose the general form of Hc(t)
H.c. The second term of the Hamiltonian (9) corresponds to the nonadiabatic couplings which may lead to an imperfect state transfer. In order to correct the nonadiabatic errors, we look for a correction Hamiltonian Hc(t) such that the modified Hamiltonian Hmod(t) = H(t) + Hc(t) governs a perfect state transfer. Here we choose the general form of Hc(t)

where we introduce  H.c., and gx(t) and gz(t) are two parameters determined later. Then the Hamiltonian (6) becomes
H.c., and gx(t) and gz(t) are two parameters determined later. Then the Hamiltonian (6) becomes

with the modified pulses

We define a new basis of dressed states  . In this scheme, we choose
. In this scheme, we choose

with an Euler angle μ(t). By moving the modified Hamiltonian (11) to the dressed-state frame defined by V(t), we obtain a new Hamiltonian

with  and the time-dependent parameters
and the time-dependent parameters 
 ,
,  and
and  . When the parameters are chosen as
. When the parameters are chosen as

the second term of the Hamiltonian (14) is removed. There will be no transition between  ,
,  and
and  . Furthermore, in the original frame, the transitions between
. Furthermore, in the original frame, the transitions between  ,
,  and
and  are canceled.
are canceled.
Next, in the original frame, we define

Obviously, |φD(t)〉 can serve as a medium state which operates a two-atom quantum state transfer |ϕ1〉 → |ϕ5〉 by setting θ(ti) = 0, θ(tf) = π/2 and μ(ti) = μ(tf) = 0, where ti(f) is the initial (final) time. Analogously, a maximum two-atom entangled state  can be generated by setting θ(ti) = 0, θ(tf) = π/4 and μ(ti) = μ(tf) = 0.
can be generated by setting θ(ti) = 0, θ(tf) = π/4 and μ(ti) = μ(tf) = 0.
Based on the process above, we have used the dressed-state method to achieve shortcuts to adiabaticity in a non-adiabatic way and implement the fast two-atom quantum state transfer and maximum entanglement generation. The evolution process is not necessarily slow and there is no direct coupling between the initial state and the target state, as long as a set of suitable dressed states is chosen.
Numerical simulations
Selections of parameters
First of all, we give numerical simulations to select appropriate parameters for insuring the experimental and theoretical feasibility. The original pulses Ω1(t) and Ω2(t) can be chosen as the Gaussian pulses1,4

and the corresponding  and
and  , the original driving pulses of the total system, can be obtained. In the scheme, we choose t0 = 3tf/40 and τ = 0.1tf. Besides, θ(tf) = π/2 and θ(tf) = π/4 are for the quantum state transfer and the entanglement generation, respectively. The Euler angle μ(t) is defined by
, the original driving pulses of the total system, can be obtained. In the scheme, we choose t0 = 3tf/40 and τ = 0.1tf. Besides, θ(tf) = π/2 and θ(tf) = π/4 are for the quantum state transfer and the entanglement generation, respectively. The Euler angle μ(t) is defined by

where G(t) = sech(t/τ) is chosen to regularize μ(t) such that it can meet the condition μ(ti) = μ(tf) = 0 and make  , the population of |ϕd〉 (see Equation (16)), as small as possible. Then based on the relevant parameters above, the modified pulses
, the population of |ϕd〉 (see Equation (16)), as small as possible. Then based on the relevant parameters above, the modified pulses  and
and  can be determined by Eq. (12). Also, the corresponding modified driving pulses of the total system
can be determined by Eq. (12). Also, the corresponding modified driving pulses of the total system  and
and  are obtained.
are obtained.
In order to choose a small and feasible value of the operation time tf, in Fig. 2, we plot the shapes of the modified pulses  and
and  with different values of tf. From Fig. 2, we can clearly find that, both for the quantum state transfer and the entanglement generation, the longer the operation time tf is, the more similar the shapes of the modified pulses are to those of the original pulses. In other words, the modified pulses’ experimental feasibility increases as the operation time tf increases, which implies the operation time we choose can not be too short. Then, taking the boundary conditions about θ(t) into account, we plot the time dependence of θ(t) in Fig. 3(a,b) for the quantum state transfer and the entanglement generation, respectively, with an arbitrary tf. Without a doubt, Fig. 3(a,b) show that the boundary conditions with respect to θ(t) can be satisfied perfectly, and the time dependence of θ(t) is independent of tf. For the boundary condition μ(ti) = μ(tf) = 0, we show it in Fig. 3(c,d) by plotting the time dependence of μ(t) with several different values of tf. Apparently, μ(ti) = μ(tf) = 0 is always satisfied well with an arbitrary tf. The maximum values of |μ(t)|, however, always decrease with the increase of tf. Therefore, for |ϕd〉 population sin2μ(t) being small enough, the operation time we choose can not be too short.
with different values of tf. From Fig. 2, we can clearly find that, both for the quantum state transfer and the entanglement generation, the longer the operation time tf is, the more similar the shapes of the modified pulses are to those of the original pulses. In other words, the modified pulses’ experimental feasibility increases as the operation time tf increases, which implies the operation time we choose can not be too short. Then, taking the boundary conditions about θ(t) into account, we plot the time dependence of θ(t) in Fig. 3(a,b) for the quantum state transfer and the entanglement generation, respectively, with an arbitrary tf. Without a doubt, Fig. 3(a,b) show that the boundary conditions with respect to θ(t) can be satisfied perfectly, and the time dependence of θ(t) is independent of tf. For the boundary condition μ(ti) = μ(tf) = 0, we show it in Fig. 3(c,d) by plotting the time dependence of μ(t) with several different values of tf. Apparently, μ(ti) = μ(tf) = 0 is always satisfied well with an arbitrary tf. The maximum values of |μ(t)|, however, always decrease with the increase of tf. Therefore, for |ϕd〉 population sin2μ(t) being small enough, the operation time we choose can not be too short.
(a,b) Time dependence of θ(t) with an arbitrary tf; (c,d) time dependence of μ(t) with some different tf. The parameters used here are the same as in Fig. 2.
For the high experimental feasibility of the scheme and a relatively small occupancy of |ϕd〉, we preselect tf = 40/Ω0. Then with tf = 40/Ω0, in Fig. 4(a), we plot the fidelities of the dressed-state scheme as functions of the atom-cavity coupling strength g, where the fidelities are defined by F = |〈ϕideal|ϕ(t)〉|2 with |ϕideal〉 = |ϕ5〉 for the state transfer or  for the entanglement generation. |ϕ(t)〉 is the state of the whole system. Because of the Zeno limit condition
for the entanglement generation. |ϕ(t)〉 is the state of the whole system. Because of the Zeno limit condition  , the fidelities increase with the increase of g/Ω0. However, as shown in Fig. 4(a), even when g = 4 Ω0 which does not strictly meet the Zeno limit condition, the fidelities are almost unit both for the quantum state transfer and the entanglement generation. Here we preselect g = 10 Ω0 to guarantee the scheme’s robustness. For checking the feasibility of the preselection tf = 40/Ω0, we plot the fidelities as functions with respect to tf in Fig. 4(b) with g = 10 Ω0, and Fig. 4(b) indicates that the preselection tf = 40/Ω0 is feasible and robust both for the quantum state transfer and the entanglement generation. Next, in Fig. 4(c), we plot the fidelities versus tf in the STIRAP scheme. Through the comparison between Fig. 4(b,c), we know that the operation time in the dressed-state scheme is just around 1/10 of that in the STIRAP scheme when the fidelities reach near 1, which indicates that the dressed-state scheme can greatly speed up the adiabatic two-atom quantum state transfer and entanglement generation.
, the fidelities increase with the increase of g/Ω0. However, as shown in Fig. 4(a), even when g = 4 Ω0 which does not strictly meet the Zeno limit condition, the fidelities are almost unit both for the quantum state transfer and the entanglement generation. Here we preselect g = 10 Ω0 to guarantee the scheme’s robustness. For checking the feasibility of the preselection tf = 40/Ω0, we plot the fidelities as functions with respect to tf in Fig. 4(b) with g = 10 Ω0, and Fig. 4(b) indicates that the preselection tf = 40/Ω0 is feasible and robust both for the quantum state transfer and the entanglement generation. Next, in Fig. 4(c), we plot the fidelities versus tf in the STIRAP scheme. Through the comparison between Fig. 4(b,c), we know that the operation time in the dressed-state scheme is just around 1/10 of that in the STIRAP scheme when the fidelities reach near 1, which indicates that the dressed-state scheme can greatly speed up the adiabatic two-atom quantum state transfer and entanglement generation.
(a) Fidelities as functions of g with tf = 40/Ω0 in the dressed-state scheme; (b) fidelities as functions of tf with g = 10 Ω0 in the dressed-state scheme; (c) fidelities as functions of tf with g = 10 Ω0 in the STIRAP scheme. Other parameters used here are the same as in Fig. 2.
Discussion of effectiveness
In this subsection, in order to show the effectiveness of the dressed-state scheme, in Fig. 5, we show the time dependence of the populations of the states |ϕ1〉 and |ϕ5〉 and the residual errors ε(t) = 1 − |〈ϕideal|ϕ(t)〉|2 of the quantum state transfer and the entanglement generation, respectively. As shown in Fig. 5(a,c), the dressed-state scheme achieves the perfect desired population transfer both for the quantum state transfer and the entanglement generation, but the STIRAP scheme can not perfectly achieve the quantum state transfer or the entanglement generation. Correspondingly, in Fig. 5(b,d), the dressed-state scheme leads to a reduction of the residual errors by over four orders of magnitude at the final time both for the state transfer and the entanglement generation. Therefore, there is no doubt that the dressed-state scheme is highly feasible and effective even within a very short operation time.
(a,c): Time dependence of the populations of the states |ϕ1〉 and |ϕ5〉 in the dressed-state scheme (thick red lines) and the STIRAP scheme (thin blue lines); (b,d): residual errors of the states in the dressed-state scheme (red dashed lines) and the STIRAP scheme (blue solid lines). g = 10 Ω0, tf = 40/Ω0 and other parameters used here are the same as in Fig. 2.
Discussion of robustness
In the above discussion, we think the operations and the whole system perfect and absolutely isolated from the environment. Therefore, it is necessary to give the discussions about the robustness of the scheme against the variations in the parameters and decoherence induced by the atomic spontaneous emissions and photon leakages from the cavity.
We first consider the robustness of the scheme against variations in the parameters of the pulse sequences by plotting the fidelity versus the variations in the pulses time tf and amplitude Ω0 in Fig. 6(a) for the two-atom state transfer based the dressed-state scheme. Here we define δx = x′ − x as the deviation of x, in which x denotes the ideal value and x′ denotes the actual value. From Fig. 6(a), we learn that the fidelity slightly decreases with the increasing amplitude Ω0. It is clear that the increase of Ω0 causes the increase of the modified pulses’ amplitudes, and thus, to a certain extent, the Zeno limit condition will be spoiled. While simultaneously we can also see that, the longer tf is, the higher the fidelity is. The reason can be deduced from Fig. 2 that when the operation time increases, the amplitudes of the modified pulses will decrease, and thus the Zeno limit condition will be met more strictly. Taking one with another, however, the fidelity always keeps near F = 1, and hence the dressed-state scheme have the extremely high robustness against the variations in tf and Ω0. Analogously, the entanglement generation has a similar situation. Dissimilarly, however, the condition sin θ(tf) = cos θ(tf) (i.e., θ(tf) = π/4) in Eq. (11) is very critical for the maximum entanglement generation. Therefore, we are supposed to consider the effect of the variations in θ(tf) on the fidelity. We plot the fidelity versus the variations in tf and θ(tf) in Fig. 6(b) for the entanglement generation based on the dressed-state scheme. To all appearances, in Fig. 6(b), the effect of the variations in θ(tf) on the fidelity is far greater than that of the variations in tf. But even so, the fidelity can keep quite high even when |δθ(tf)/θ(tf)| = 0.1. To sum up, the dressed-state scheme are robust against variations in the parameters of the pulse sequences.
(a) The fidelity versus the variations in the pulses time tf and amplitude Ω0 for the state transfer; (b) the fidelity versus the variations in tf and θ(tf) for the entanglement generation. The parameters used here are same as in Fig. 5.
Next, we take the decoherence induced by the atomic spontaneous emissions and the photon leakage from the cavity into account. Then the whole system is dominated by the master equation

where  ;
;  is the spontaneous emission rate of jth atom from the excited state |2〉j to the ground state |i〉j; κ denotes the photon leakage rate from the cavity;
is the spontaneous emission rate of jth atom from the excited state |2〉j to the ground state |i〉j; κ denotes the photon leakage rate from the cavity;  . For simplicity, we assume
. For simplicity, we assume  . By means of the master equation, we plot the fidelities for the state transfer and the entanglement generation versus κ/Ω0 and γ/Ω0 in Fig. 7. Firstly, in Fig. 7, we can see that the fidelities for the state transfer and the entanglement generation are over 0.95 and 0.985, respectively, even when κ = γ = 0.1 Ω0. Without a doubt, the dressed-state scheme for the state transfer or the entanglement generation is robust against the decoherence induced by the atomic spontaneous emissions and the photon leakage from the cavity. In addition, as seen from the decrease of the fidelities with the increases of κ and γ in Fig. 7, we learn that the influence of the atomic spontaneous emissions on the fidelity is obviously greater than that of the photon leakages from the cavity. Even in Fig. 7(a), for the state transfer, the influence of the atomic spontaneous emissions on the fidelity almost plays a full role, but that of the photon leakages from the cavity is little. It follows that the dressed-state scheme we propose has the robustness against the photon leakages from the cavity more than the atomic spontaneous emissions.
. By means of the master equation, we plot the fidelities for the state transfer and the entanglement generation versus κ/Ω0 and γ/Ω0 in Fig. 7. Firstly, in Fig. 7, we can see that the fidelities for the state transfer and the entanglement generation are over 0.95 and 0.985, respectively, even when κ = γ = 0.1 Ω0. Without a doubt, the dressed-state scheme for the state transfer or the entanglement generation is robust against the decoherence induced by the atomic spontaneous emissions and the photon leakage from the cavity. In addition, as seen from the decrease of the fidelities with the increases of κ and γ in Fig. 7, we learn that the influence of the atomic spontaneous emissions on the fidelity is obviously greater than that of the photon leakages from the cavity. Even in Fig. 7(a), for the state transfer, the influence of the atomic spontaneous emissions on the fidelity almost plays a full role, but that of the photon leakages from the cavity is little. It follows that the dressed-state scheme we propose has the robustness against the photon leakages from the cavity more than the atomic spontaneous emissions.
The fidelity as a function of γ/Ω0 and κ/Ω0.The parameters used here are the same as in Fig. 5.
We have chosen the Zeno limit condition  to restrain the population of the cavity-mode excited state |ϕ3〉. Besides, we have known that the increase of the operation time tf leads to the decrease of |μ(t)|max from Fig. 3(b), and thus leads to the decrease of |ϕd〉 population sin2μ(t). Therefore, the influence of the photon leakages from the cavity and the atomic spontaneous emissions on the fidelity should be restrained by a bigger g and a longer tf, respectively. Based on this, we plot the fidelities as the functions with respect to g and κ in Fig. 8(a,c) for the state transfer and the entanglement generation, respectively. Clearly, when the photon leakages from the cavity exist, a bigger value of g can greatly depress the influence of the photon leakages from the cavity on the fidelities. In Fig. 8(b,d), we plot the fidelities as the functions with respect to tf and γ for the state transfer and the entanglement generation, respectively. Also clearly, when the atomic spontaneous emissions exist, the influence of the atomic spontaneous emissions on the fidelities can be restrained by a longer tf. Nevertheless, for the experimental feasibility and the efficiency of the scheme, we pick an appropriate pair of values g = 10 Ω0 and tf = 40/Ω0.
to restrain the population of the cavity-mode excited state |ϕ3〉. Besides, we have known that the increase of the operation time tf leads to the decrease of |μ(t)|max from Fig. 3(b), and thus leads to the decrease of |ϕd〉 population sin2μ(t). Therefore, the influence of the photon leakages from the cavity and the atomic spontaneous emissions on the fidelity should be restrained by a bigger g and a longer tf, respectively. Based on this, we plot the fidelities as the functions with respect to g and κ in Fig. 8(a,c) for the state transfer and the entanglement generation, respectively. Clearly, when the photon leakages from the cavity exist, a bigger value of g can greatly depress the influence of the photon leakages from the cavity on the fidelities. In Fig. 8(b,d), we plot the fidelities as the functions with respect to tf and γ for the state transfer and the entanglement generation, respectively. Also clearly, when the atomic spontaneous emissions exist, the influence of the atomic spontaneous emissions on the fidelities can be restrained by a longer tf. Nevertheless, for the experimental feasibility and the efficiency of the scheme, we pick an appropriate pair of values g = 10 Ω0 and tf = 40/Ω0.
(a,c): The fidelities as functions of g/Ω0 and κ/Ω0 with tf = 40/Ω0 and γ = 0; (b,d): the fidelities as functions of  and γ/Ω0 with g = 10 Ω0 and κ = 0. Other parameters used here are the same as in Fig. 2.
and γ/Ω0 with g = 10 Ω0 and κ = 0. Other parameters used here are the same as in Fig. 2.
Experimentally, it is too hard to have the theoretically predicted values of the parameters. Therefore, in Fig. 9, we give the numerical simulations to discuss the joint effects of the photon leakages from the cavity and the variations in the atom-cavity coupling strength g = 10 Ω0 and those of the atomic spontaneous emissions and the variations in the operation time tf = 40/Ω0 on the fidelities. Figure 9(a,c) also indicate that when the photon leakages from the cavity exist, a bigger value of g can greatly depress the influence of the photon leakages from the cavity on the fidelities. Although either κ or the variations in g can not be controlled in experiment, the fidelities are over 0.99 even under the terrible condition {δg/g = −0.1, κ = 0.1 Ω0}. Figure 9(b,d) show that the fidelities are almost not affected by the variations in tf = 40/Ω0 whenever the atomic spontaneous emissions exist or not. In other words, the dressed-state scheme are extremely robust against the variations in the chosen operation time. In addition, once the operation time is determined, the effects of the atomic spontaneous emissions on the fidelities are independent on the variations in the operation time.
(a,c): The fidelities versus κ/Ω0 and the variations in g with γ = 0; (b,d): the fidelities versus γ/Ω0 and the variations in tf with κ = 0. The parameters used here are the same as in Fig. 5.
Conclusion
In conclusion, we have developed the dressed-state method to speed up the adiabatic quantum state transfer and entanglement generation between two Λ-type atoms trapped in an optical cavity. There is no a direct coupling of the target state and the initial state appearing in the Hamiltonian. The pulses are modified with the high experimental feasibility. During the whole evolution, the adiabatic condition is not necessary to be met, and thus even within a very short operation time, the state transfer and the entanglement generation can be achieved with quite high fidelities. The introductions of the Zeno limit condition and the auxiliary function G(t) restrain the populations of all of the excited states and hence the scheme is robust against the decoherence induced by the atomic spontaneous emissions and the photon leakage from the cavity. Besides, the results of the numerical simulations show that the dressed-state scheme is robust against the variations in the chosen parameters.
Based on ref. 46, by using cesium atoms and a set of cavity-QED predicted parameters (g, κ, γ)/2π = (750, 3.3, 2.62) MHz, we can achieve the two-atom quantum state transfer and maximum entanglement generation with the fidelities F = 0.985 and F = 0.996, respectively. Therefore, it allows us to construct an atomic system for the quantum state transfer and the entanglement generation in the presence of decoherence. In a word, by using dressed states, we have implemented the fast, feasible and robust two-atom adiabatic quantum state transfer and entanglement generation. In the further work, it could be interesting to apply the dressed-state method to more complex systems for preparing more complex entanglement and constructing quantum gates.
Additional Information
How to cite this article: Wu, J.-L. et al. Fast adiabatic quantum state transfer and entanglement generation between two atoms via dressed states. Sci. Rep. 7, 46255; doi: 10.1038/srep46255 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Bergmann, K., Theuer, H. & Shore, B. W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 70, 1003 (1998).
Lee, J., Paternostro, M., Kim, M. S. & Bose, S. Entanglement reciprocation between qubits and continuous variables. Phys. Rev. Lett. 96, 080501 (2006).
Kimble, H. J. The quantum internet. Nature 453, 1023 (2008).
Vitanov, N. V., Suominen, K. A. & Shore, B. W. Creation of coherent atomic superpositions by fractional stimulated Raman adiabatic passage. J. Phys. B: At. Mol. Opt. Phys. 32, 4535 (1999).
Vitanov, N. V., Halfmann, T., Shore, B. W. & Bergmann, K. Laser-induced population transfer by adiabatic passege techniques. Annu. Rev. Phys. Chem. 52, 763 (2001).
Muga, J. G., Chen, X., Ruschhaupt, A. & Guéry-Odelin, D. Frictionless dynamics of Boseš CEinstein condensates under fast trap variations. J. Phys. B 42, 241001 (2009).
Chen, X., Lizuain, I., Ruschhaupt, A., Guéry-Odelin, D. & Muga, J. G. Shortcut to adiabatic passage in two- and three-level atoms. Phys. Rev. Lett. 105, 123003 (2010).
Ibáñez, S., Martínez-Garaot, S., Chen, X., Torrontegui, E. & Muga, J. G. Shortcuts to adiabaticity for non-Hermitian systems. Phys. Rev. A 84, 023415 (2011).
Ibáñez, S., Chen, X., Torrontegui, E., Muga, J. G. & Ruschhaupt, A. Multiple Schrödinger pictures and dynamics in shortcuts to adiabaticity. Phys. Rev. Lett. 109, 100403 (2012).
Torrontegui, E. et al. Shortcuts to adiabaticity. Adv. At., Mol., Opt. Phys. 62, 117 (2013).
del Campo, A. Shortcuts to adiabaticity by counterdiabatic driving. Phys. Rev. Lett. 111, 100502 (2013).
Kiely, A. & Ruschhaupt, A. Inhibiting unwanted transitions in population transfer in two- and three-level quantum systems. J. Phys. B. 47, 115501 (2014).
Ibáñez, S., Li, Y. C., Chen, X. & Muga, J. G. Pulse design without the rotating-wave approximation. Phys. Rev. A. 92, 062136 (2015).
Zhang, J., Kyaw, T. H., Tong, D. M., Sjöqvist, E. & Kwek, L. C. Fast non-Abelian geometric gates via transitionless quantum driving. Sci. Rep. 5, 18414 (2015).
Song, X. K., Zhang, H., Ai, Q., Qiu, J. & Deng, F. G. Shortcuts to adiabatic holonomic quantum computation in decoherence-free subspace with transitionless quantum driving algorithm. New J. Phys. 18, 023001 (2016).
Chen, Y. H., Xia, Y., Wu, Q. C., Huang, B. H. & Song, J. Method for constructing shortcuts to adiabaticity by a substitute of counterdiabatic driving terms. Phys. Rev. A 93, 052109 (2016).
Song, X. K., Ai, Q., Qiu, J. & Deng, F. G. Physically feasible three-level transitionless quantum driving with multiple Schrodinger dynamics. Phys. Rev. A 93, 052324 (2016).
Song, X. K., Deng, F. G., Lamata, L. & Muga, J. G. Robust state preparation in quantum simulations of Dirac dynamics. Phys. Rev. A 95, 022332 (2017).
Bason, M. G. et al. High-fidelity quantum driving. Nat. Phys. 8, 147 (2012).
Zhang, J. et al. Experimental implementation of assisted quantum adiabatic passage in a single spin. Phys. Rev. Lett. 110, 240501 (2013).
Du, Y. X. et al. Experimental realization of stimulated Raman shortcut-to-adiabatic passage with cold atoms. Nat. Commun. 7, 12479 (2016).
An, S., Lv, D., del Campo, A. & Kim, K. Shortcuts to adiabaticity by counterdiabatic driving for trapped-ion displacement in phase space. Nat. Commun. 7, 12999 (2016).
Zhou, B. B. et al. Accelerated quantum control using superadiabatic dynamics in a solid-state lambda system. Nat. Phys., doi: 10.1038/nphys3967 (2016).
Demirplak. M. & Rice, S. A. Adiabatic population transfer with control fields. J. Phys. Chem. A 107, 9937 (2003).
Demirplak, M. & Rice, S. A. On the consistency, extremal, and global properties of counterdiabatic fields. J. Chem. Phys. 129, 154111 (2008).
Berry, M. V. Transitionless quantum driving. J. Phys. A 42, 365303 (2009).
Lewis, H. R. & Riesenfeld, W. B. An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field. J. Math. Phys. (N.Y.) 10, 1458 (1969).
Chen, X. & Muga, J. G. Engineering of fast population transfer in three-level systems. Phys. Rev. A 86, 033405 (2012).
Giannelli, L. & Arimondo, E. Three-level superadiabatic quantum driving. Phys. Rev. A 89, 033419 (2014).
Masuda, S. & Rice, S. A. Fast-forward assisted STIRAP. J. Phys. Chem. A 119, 3479 (2015).
Lu, M., Xia, Y., Shen, L. T., Song, J. & An, N. B. Shortcuts to adiabatic passage for population transfer and maximum entanglement creation between two atoms in a cavity. Phys. Rev. A 89, 012326 (2014).
Chen, Y. H., Xia, Y., Song, J. & Chen, Q. Q. Shortcuts to adiabatic passage for fast generation of Greenberger–Horne–Zeilinger states by transitionless quantum driving. Sci. Rep. 5, 15616 (2015).
Chen, Z., Chen, Y. H., Xia, Y., Song, J. & Huang, B. H. Fast generation of three-atom singlet state by transitionless quantum driving. Sci. Rep. 6, 22202 (2016).
Chen, Y. H., Xia, Y., Chen, Q. Q. & Song, J. Efficient shortcuts to adiabatic passage for fast population transfer in multiparticle systems. Phys. Rev. A 89, 033856 (2014).
Chen, Y. H., Xia, Y., Chen, Q. Q. & Song, J. Fast and noise-resistant implementation of quantum phase gates and creation of quantum entangled states. Phys. Rev. A 91, 012325 (2015).
Liang, Y., Wu, Q. C., Su, S. L., Ji, X. & Zhang, S. Shortcuts to adiabatic passage for multiqubit controlled-phase gate. Phys. Rev. A 91, 032304 (2015).
Liang, Y., Song, C., Ji, X. & Zhang, S. Fast CNOT gate between two spatially separated atoms via shortcuts to adiabatic passage. Opt. Express 23, 23798 (2015).
Liang, Y., Ji, X., Wang, H. F. & Zhang, S. Deterministic SWAP gate using shortcuts to adiabatic passage. Laser Phys. Lett. 12, 115201 (2015).
Baksic, A., Ribeiro, H. & Clerk, A. A. Speeding up adiabatic quantum state transfer by using dressed states. Phys. Rev. Lett. 116, 230503 (2016).
Kang, Y. Y., Chen, Y. H., Shi, Z. C., Song, J. & Xia, Y. Fast preparation of W states with superconducting quantum interference devices by using dressed states. Phys. Rev. A 94, 052311 (2016).
Facchi, P. & Pascazio, S. Quantum Zeno Subspaces. Phys. Rev. Lett. 89, 080401 (2002).
Facchi, P., Marmo, G. & Pascazio, S. Quantum Zeno dynamics and quantum Zeno subspaces. J. Phys: Conf. Ser. 196, 012017 (2009).
Shao, X. Q., Chen, L., Zhang, S. & Yeon, K. H. Fast CNOT gate via quantum Zeno dynamics. J. Phys. B: At. Mol. Opt. Phys. 42, 165507 (2009).
Shao, X. Q. et al. Converting two-atom singlet state into three-atom singlet state via quantum Zeno dynamics. New J. Phys. 12, 023040 (2010).
Shao, X. Q., Chen, L., Zhang, S., Zhao, Y. F. & Yeon, K. H. Deterministic generation of arbitrary multi-atom symmetric Dicke states by a combination of quantum Zeno dynamics and adiabatic passage. Europhys. Lett. 90, 50003 (2010).
Spillane, S. M. et al. Ultrahigh-Q toroidal microresonators for cavity quantum electrodynamics. Phys. Rev. A 71, 013817 (2005).
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grants No. 11464046 and No. 61465013.
Author information
Authors and Affiliations
Contributions
J.L.W. designed the scheme under the guidance of X.J. and S.Z.. All authors contributed to the interpretation of the work and the writing of the manuscript. All authors participated in the writing and revising of the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wu, JL., Ji, X. & Zhang, S. Fast adiabatic quantum state transfer and entanglement generation between two atoms via dressed states. Sci Rep 7, 46255 (2017). https://doi.org/10.1038/srep46255
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep46255
This article is cited by
-
Efficient Generation of W Entangled States Among Superconducting Qubits via Lie-Algebra–Based Transforms
International Journal of Theoretical Physics (2023)
-
A protocol to create a multi-particle entangled state for quantum-enhanced sensing
Indian Journal of Physics (2023)
-
Optimal controls of invariant-based population transfer in a superconducting qutrit
Quantum Information Processing (2020)
-
Superadiabatic Shortcuts for Fast Generating Two-Atom Four-Dimensional Entanglement
International Journal of Theoretical Physics (2019)
-
Generation of W state by combining adiabatic passage and quantum Zeno techniques
Indian Journal of Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

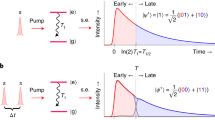


 and
and  with several different values of the operation time tf. The parameters used here are t0 = 3tf/40, τ = 0.1tf, θ(tf) = π/2 for the quantum state transfer or θ(tf) = π/4 for the entanglement generation.
with several different values of the operation time tf. The parameters used here are t0 = 3tf/40, τ = 0.1tf, θ(tf) = π/2 for the quantum state transfer or θ(tf) = π/4 for the entanglement generation.





