Introduction

Perovsike nickelates RNiO3 (R = rare earth) provide a remarkable example of materials to achieve a good understanding of the interdependence between structural, electronic and magnetic properties by simply changing the R cation1,2. Except for R = La, the materials of the RNiO3 series exhibit steep metal-insulator (MI) transition and antiferromagnetic ordering3,4. The MI transition can be tuned by chemical doping5,6,7, applied hydrostatic pressures8,9,10 and electric field11, which opens new opportunities for future electronic devices12,13. According to the diagram proposed by Zaanen et al.14, RNiO3 lies in the charge-transfer region in which the band gap between the nickel 3d-band and the oxygen p-band is smaller than the on-site Coulomb interaction (Udd). The change of both Ni-O-Ni bond angle and NiO length bond with increasing temperature reduces the band gap, hence leading to a metallic phase. Some studies have shown that charge ordering plays a role in the MI transition. Indeed, a long-range charge imbalance characterized by the parameter δ, i.e. has been observed in the insulating regime, while nickel is uniformly trivalent in the metallic state15,16,17. On the other hand, the elements of RNiO3 have been classified as small or negative charge transfer systems18,19,20. In this case, some holes are transferred from the 3d orbitals to the 2p orbitals and the ground state can thus be described as a mixture of d7 and d8L configurations instead of the purely ionic d7 configuration. Recent dynamical mean field theory (DMFT) calculations mention the importance of ligand holes in the electronic structure. For example, Park et al.19 explained the insulating phase as a “site-selective” Mott phase associated with long bound sites while Johnston et al.21 suggest a novel charge ordering , where S is the total spin. According to this picture, the long-bond octahedra are associated with the d8 configuration (with a large local moment) and the short-bond ones with (with the Ni local moment screened by the two ligand holes). Furthermore, the charge ordering is achieved without any significant movement of charge21.

The crystallization of bulk RNiO3 in the perovskite structure is normally achieved at high temperatures and oxygen pressures. However, another way to stabilize the nickelate phase is to use the template effect of a perovskite substrate with minimal lattice mismatch. Several research groups are interested to understand the relationship between the nature of epitaxial strain and the MI transition due to changes in the nickel oxidation state. For example, in-plane compressive strain maintains the oxidation state in the SNO films, resulting in a steep MI transition22,23. On the other hand, the tensile strain induces the creation of oxygen vacancies, which leads to the annihilation of the MI transition. This has been observed for example in the case of epitaxial SNO grown on SrTiO3 (STO) substrate24,25. However, our team has recently demonstrated the capability to grow epitaxial SNO thin films under tensile strain on STO substrate with a steep MI transition at about 394 K26.

In this work, we examine how the strain relaxation (compressive/tensile) affects the electronic properties of epitaxial SNO thin films grown on LaAlO3 (LAO, compressive) and STO (tensile) as well as their optical characteristics in the UV-visible and infrared spectrum.

Results

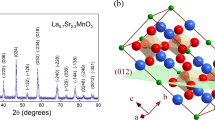
At room temperature, bulk SNO possesses an orthorhombic (orth) structure and lattice parameters a0 = 5.328 Å, b0 = 5.437 Å and c0 = 7.567 Å. The SNO unit cell can be described by a pseudo-cubic unit with apc = 3.799 Å, yielding a volume of 54.82 Å3 27. The LAO (001) and STO substrates (001) provide −0.26% (compressive strain) and +2.7% (tensile strain) lattice mismatch, respectively. Figure 1a displays the x-ray pattern of SNO thin films of thickness equal to 8.5 (SNO1L), 16 (SNO2L) and 63 nm (SNO3L) grown on LAO substrates (see definitions of SNO exponents in the Methods section). We only observe the (00 L) reflection of LAO due to its very close lattice match with SNO. For the samples grown on STO (Fig. 2a), the sole presence of (00 L) peaks of SNO and STO in the x-ray diffraction scans indicates a textured growth. In Fig. 2, Laue fringes are clearly visible for the SNO1S and SNO2S samples. Their presence indicates a uniform thickness with two well–defined interfaces (SNO/STO and SNO/Air). In order to investigate the epitaxial relation between SNO and STO, XRD φ measurements were performed on the (111)SNOorth/(011)LAOpc and (111)STO/(111)SNOpc reflections (Figs 1b and 2c). The SNO peaks are superimposed with those from the LAO (Fig. 1b) and STO (Fig. 2c) substrates confirming the cube-on-cube growth of our films. In addition, the atomic force microscopy (AFM) images of 8.5 nm-thick SNO films grown on LAO and STO (data not presented here) show atomically smooth surfaces with a root mean square (RMS) roughness of ~0.2 nm and ~0.3 nm, respectively.

Figure 1
figure 1

(a) XRD spectra of SNO thin films on LAO with different film thicknesses. (b) φ scans performed on (011) pseudocubic reflection of LAO and (111) orthorhombic reflection of SNO.

Full size image
Figure 2
figure 2

(a) X-ray spectra of SNO films grown on STO with different film thicknesses. (b) details of the X-ray spectra around the (001) peak of SNO films grown on STO. (c) φ scans performed on (111)STO and (111)SNOpc reflections.

Full size image

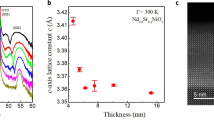
To analyse the strain behaviour of the films grown on STO, we measured the reciprocal space maps (RSM) asymmetrical Bragg reflection (103) as illustrated in Fig. 3a to Fig. 3c. Figure 3d shows the dependence of the lattice parameters on the film thickness. From this figure, it can be concluded that the film thickness significantly influences the strain state of the SNO films deposited on STO. For the SNO1S sample, the in-plane lattice parameter is larger than the bulk value while the out-of-plane lattice parameter is lower. As the film thickness increases, the SNO film strain reduces so that both in-plane and out-of-plane lattice parameters tend towards their bulk values.

Figure 3
figure 3

(a–c) Reciprocal lattice maps around (103) Bragg reflections of SNO thin films on STO with different film thicknesses. (d) Lattice parameters for SNO films on STO as a function of thickness.

Full size image

The temperature dependence of the resistivity of SNO films grown on LAO and STO is shown in Fig. 4a and c, respectively. All the samples exhibit a MI transition. The temperature corresponding to the MI transition is attained when the sign of the resistivity derivative changes (see Fig. 4b and d). For SNO films under compressive strain (i.e. grown on LAO), values of TMI equal to 381 K, 383 K and 370 K are obtained for SNO1L, SNO2L and SNO3L, respectively. These transition temperatures are consistent with those reported in previous studies28,29,30. Recently, theoretical calculations have revealed that compressive strain is reduced by straightening the Ni-O-Ni angle, which increases the orbital overlap and modifies the bandwidth. Such bond straightening leads to a continuous shift of the MIT from TMI = 400 K to TMI = 0 K30.

Figure 4
figure 4

Temperature dependence of the resistivity for SNO thin films on LAO (a) and STO (c) substrates. Derivative of resistivity of SNO films on LAO (b) and STO (d). TMI corresponds to the temperature at which the sign of changes and its uncertainty is defined by the temperature step size, 5 K.

Full size image

For the SNO films under tensile strain grown on STO, the MI transition is found to be about 396 K, 406 K and 404 K for SNO1S, SNO2S and SNO3S, respectively. Furthermore, we observe that the MI transition is broader while the metallic state is significantly resistive, particularly for the sample SNO1S. It is well known the oxygen non-stoichiometry results in an expansion of the cell volume and is accompanied by the suppression of MI transition25,31. Compared to the unit cell of SNO bulk (volume of 54.8 Å3), the thinner sample SNO1S exhibits a larger volume (56.54 Å3), which suggests that the creation of oxygen vacancies is the mechanism leading to tensile strain and that the oxygen vacancies are mainly close to the interface SNO/STO32. When the sample thickness is increased, the unit cell volume of SNO2S and SNO3S shrinks to 55.1 and 54.75 Å3, respectively. These values are close to that of the stoichiometric bulk sample, which suggests that the amount of oxygen vacancies in the films has become negligible. This observation indicates that mechanical rather than chemical relaxation (oxygen vacancies) is the dominant mechanism of strain relaxation. Therefore, it can be concluded that the tensile strain generated at the interface reduces the Ni-O-Ni bond angle unlike the case of compressive strain and increases the buckling of the NiO6 octahedra, which results in less orbital overlap, i.e. in a narrowing of the d-band33,34.

In Fig. 5, the real part of the optical conductivity σ1(ω) of the all samples is displayed as a function of the photon energy for different values of the temperature. The optical conductivity is related to the complex dielectric function though the equation . For all the samples, a Drude contribution and four peaks (A, B, C, and D) corresponding to interband transitions can be identified. According to the band structure calculations for SNO crystal35, we suggest that the A and B features are due to the transitions between the occupied and unoccupied e*g orbitals. The excitations from the t*g and the nonbonding O2p to the e*g orbitals are denominated C. The optical conductivity of the various samples spectra is remarkably different at high energy. For example, at 4 eV, the D peak is evident only for the thinner film SNO1S grown on STO. It can be attributed to a transition between t2g and e*g levels.

Figure 5
figure 5

Optical conductivity as a function of photon energy for SNO thin films on LAO (a–c) and on STO (d–f) substrates at different temperatures.

Full size image

In the case of SNO grown on LAO, the Drude-like peak present at very low energy disappears rapidly when the temperature is decreased towards 303 K while a new peak (denoted as A’ in Fig. 5) emerges at 0.6 eV. The transfer of spectral weight (SW) from the Drude resonance to finite energy peak is characteristic of charge-ordered systems with a weak electron-lattice coupling36,37. Indeed, Stewart et al. have concluded that both charge ordering and Mott physics occur in the insulating state for NdNiO3 thin film on STO substrate38. Furthermore, the recent DMFT calculations of bulk SNO at low temperature enable us to identify the dominant features of the optical conductivity. Indeed, Ruppen et al.39 demonstrated the peak B (1.4 eV) is due to the optical transition across the Peierls pseudogap, while the peak A’ corresponds to the transition across the insulating gap. The presence of these peaks results from the combined effect of bond disproportionation and Mott physics associated with half of the disproportionated sites39.

To determine the changes driven by the temperature in the electronic structure across the MI transition of the SNO films, we have estimated the effective number of free carriers (Neff) defined as:

Here, m0 is the free electron mass and N the number of Ni atoms per unit volume, while ωc is the cut-off frequency. The values of ωc are indicated in Fig. 5 for each sample. Figures 6a and b show the value of Neff as a function of temperature for the samples SNO on LAO and STO, respectively. As it can be seen, in both cases, Neff reaches a saturation value close to 388 K. Below 388 K, Neff decreases with decreasing temperature due to the gap formation40. The number of electrons localized at the MI transition can be calculated as . For the films deposited on LAO, we obtain values of ΔNeff = 0.026, 0.027 and 0.054 for SNO1L, SNO2L and SNO3L, respectively. For those deposited on STO, we obtain 0.009, 0.027 and 0.028 for SNO1S, SNO2S and SNO3S respectively. The conduction properties in the metallic state are correlated to ΔNeff, which represents the spectral weight . Assuming one conduction electron per Ni site, this value yields an effective mass where m* is the effective mass of conduction carriers. A small value of ΔNeff corresponds a larger , which characterizes a narrow conduction band composed of Ni 3d and O2p levels, and to larger mass enhancement by strong electron-correlation effects. The mass enhancement is higher in the SNO films on STO (tensile strain) comparatively to the films grown on LAO (compressive strain).

Figure 6
figure 6

Temperature dependence of the effective number of electrons per atom of Ni for SNO films on LAO (a) and on STO (b).

Full size image

Discussion

The strain relaxation of the SNO films changes the lattice constants, which results in modifications of the Ni-O and Sm-O bonds lengths and/or of the Ni-O-Ni band angle. Such variation of the SNO unit cell leads to modifications of the electron bandwidth and influences the electrical transport and infrared optical properties. In-plane compressive strain maintains the oxidation state in the SNO films, resulting in a steep MI transition. The decrease of TMI when the film thickness increases indicates that the SNO lattice is still able to sustain the epitaxial constraint by straightening the Ni-O-Ni angle, which broadens the bandwidth of the system.

As for the tensile relaxation characterizing SNO films deposited on STO, it is accompanied by the formation of oxygen vacancies at the interface. In our case, all the corresponding films exhibit a MI transition close to 400 K but smeared as compared to SNO deposited on LAO. Let us emphasize that in the literature, the role of oxygen vacancies in the perovskites nickelates is unclear whether the vacancies increase TMI41 or leave it unaffected31. The enhanced tensile strain associated with increasing film thickness is consistent with a narrowing of the band and an increase of the electron correlations. This tensile strain is accommodated by buckling of the NiO6 octahedra, which results in reduced orbital overlap and in the Drude spectral weight in the metallic state.

Methods

In this study, SNO thin films were grown on c- axis oriented LAO and STO single crystal substrates by pulsed laser ablation of a stoichiometric target (99.99% Kurt J. Lesker). To ensure atomically flat terraces, STO substrates were etched for 30 s in buffered HF solution (NH4F: HF = 6:1), rinsed with distilled water and dried under a nitrogen stream. Finally, the substrates were heated at 1050 °C for 30 min in an oxygen flow. In the case of LAO, the substrates were annealed at 1100 °C for 12 h in a flowing O2 atmosphere. The samples were prepared in a high vacuum deposition system filled with an oxygen pressure of 300 mTorr. The laser fluence on the target was 2 J/cm2 while the substrate temperature was kept at 600 °C during the deposition. The SNO films were in situ annealed during 30 min and cooled at 5 °C/min at the same oxygen pressure. We characterized six samples denoted by SNO1x, SNO2x and SNO3x, where , of thickness equal to 8.5 ± 0.4, 16 ± 0.2 and 63 ± 0.2 nm, respectively. Cross-sectional electron microscopy and x-ray reflectivity were used to determine the film thickness. The films structure and the epitaxial relationship with substrate were examined by four-circles x-ray diffraction (XRD). The resistivity of the thin films was measured as a function of the temperature from 235 to 463 K using the four-probe method. The resistivity ρ is deduced from the resistance by.

where t is the film thickness.

The optical characterization of the bare substrates and of the films was performed with two commercial Woollam ellipsometers from 40 meV to 4.13 eV. The Vase model based on a grating monochromator, covers the energy range between 0.62 and 4.13 eV, while the IR-Vase model was used for the range 0.04–0.61 eV. The measurements were carried out in the reflectivity configuration at an angle of incidence of 70° Spectroscopy ellipsometry converts the polarization state of the reflected light in two parameters ψ and Δ, which are related to the optical and structure properties of the samples, and defined by

Where and are the Fresnel reflection coefficients for p- and s- polarized light respectively. The experimental and best-fit calculated ellipsometry spectra for both ψ and Δ are displayed in Fig. 7a and b for the STO substrate, respectively. The corresponding results for SNO films on STO are shown in Fig. 7c and d.

Figure 7
figure 7

Experimental and best-fit calculated ellipsometry spectra of the STO substrate for ψ (a) and Δ (b) and of SNO films on STO for ψ (c) and Δ (d).

Full size image

The complex optical constants (subsequently the complex conductivities) of the SNO films were obtained by fitting numerically the data with a multilayers model involving the STO substrate, the SNO film and the transition layer. As LAO and STO have several far infrared phonons with strong temperature dependence, the samples and the substrates were measured and modeled at the same temperature. This allowed us to deduce accurate values of the complex conductivity of the SNO films from the fit of experimental data.

Additional Information

How to cite this article: Torriss, B. et al. Metal-Insulator Transition of strained SmNiO3 Thin Films: Structural, Electrical and Infrared Optical Properties. Sci. Rep. 7, 40915; doi: 10.1038/srep40915 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.