Optimization-based design of a heat flux concentrator

Abstract

To gain control over the diffusive heat flux in a given domain, one needs to engineer a thermal metamaterial with a specific distribution of the generally anisotropic thermal conductivity throughout the domain. Until now, the appropriate conductivity distribution was usually determined using transformation thermodynamics. By this way, only a few particular cases of heat flux control in simple domains having simple boundary conditions were studied. Thermal metamaterials based on optimization algorithm provides superior properties compared to those using the previous methods. As a more general approach, we propose to define the heat control problem as an optimization problem where we minimize the error in guiding the heat flux in a given way, taking as design variables the parameters that define the variable microstructure of the metamaterial. In the present study we numerically demonstrate the ability to manipulate heat flux by designing a device to concentrate the thermal energy to its center without disturbing the temperature profile outside it.

Introduction

The control of the electromagnetic flux using metamaterials led to major innovations in electronics and communications¹. Taking advantage of the analogies between electromagnetism and thermodynamics, some researchers developed materials with unprecedented thermal properties (the thermal “metamaterials”) for heat flux manipulation, for instance the heat flux inverter by Narayana and Sato².

Compared to the advances in electromagnetism, the design of thermal metamaterials is an emerging research and development area. In a first approach, metamaterials can be empirically designed (e.g., the thermal shield of Narayana and Sato²). More sophisticated thermal metamaterials can be designed using the transformation thermodynamics concept (e.g., the inverter and the concentrator proposed by Narayana and Sato² or the cloaking device of Schittny et al.³, inherited from electromagnetism⁴). A straightforward example of the application of ideas from electromagnetism in thermal problems is the heat flux inverter of Narayana and Sato², derived from the device to rotate electromagnetic fields proposed by Chen and Chan⁵ to rotate electromagnetic fields.

The transformation-based approach has been applied to specific heat control problems. For general problems (i.e., having arbitrary prescribed magnitude and direction of the heat flux, geometry of the manipulating device, geometry and boundary conditions of the domain where the device is embedded) we propose a new, optimization-based approach for the design of thermal metamaterials. A variety of optimization algorithms have been used to design efficient metamaterials but only in the field of photonic^6,7,8,9,10. Here we solve a nonlinear constrained optimization problem where the objective function to minimize is the error in the accomplishment of the given heat manipulation task, and the design variables characterize the spatial distribution of the metamaterial throughout the manipulating device.

We show the capability of the present method by designing a device for thermal concentration, as alternative to the transformation-based design of Chen and Lei¹¹, using an interior point optimization algorithm.

Definition of the heat flux guidance problem

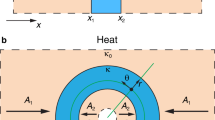
Let us consider the domain Ω in Fig. 1, with boundary ∂Ω divided in two non-overlapping portions: ∂Ω_q (where the heat flux q_wall is prescribed) and ∂Ω_T (where the temperature T_wall is prescribed). In steady state, the heat flux conduction in Ω is governed by the equation

Figure 1

Thermal problem in a macroscopic domain Ω where the effective properties depend on a quantitatively characterized microstructure.

and the boundary conditions:

where T is the temperature, s is the internal heat source, k is the (effective) thermal conductivity tensor, and n is the unit vector normal to and pointing outwards ∂Ω.

Using the finite element method (FEM), the temperature field in Ω is approximated as follows:

where N_j is the shape function associated to the node j of the finite elements mesh (discretized Ω) and T_j is the temperature at node j (unknown). Using a standard (Galerkin) FEM, the nodal temperature T_j is the solution of the algebraic system of equations

where K_ij and F_i are the components of the global conductivity matrix and the nodal heat flux vector respectively, given by

The system of equations (5) is the FEM version of the heat conduction (1) subject to the boundary conditions (2) and (3). This is a classical FEM problem, whose solution has been extensively detailed in classical FEM literature, for instance in the book of Zienkiewicz and Taylor on the basics of FEM¹².

Influence of the inhomogeneous microstructure on the macroscopic thermal response

Let the microstructure vary throughout Ω and be sampled at a series of points x^(μ) ∈ Ω (μ = 1, …, N). Further, let the microstructure at any x^(μ) be characterized by n parameters , grouped in the vector p^(μ). Then, the effective conductivity k at x^(μ) is at last a function of p^(μ), i.e.

The microstructure throughout Ω is characterized by the vector P = [p⁽¹⁾, …, p^(N)]. Then, the global conductivity matrix K (whose components are given by equation (6)) is a function of P, and so they are the nodal temperatures T_j (solution of equation (5)) and the temperature field T (approximated by equation (4) for FEM).

Task accomplishment as an optimization problem

To design the microstructure in the macroscopic domain Ω consists of finding P such that Ω responds in a desired way. In this case, we aim to enforce the heat flux to take the magnitude as well as the direction of the vector at a series of points x^(q) ∈ Ω, q = 1, …, Q, as shown in Fig. 2. The heat flux at any x^(q) is given by

Figure 2

The heat flux guidance problem in the macroscopic domain Ω; denotes the desired heat flux at the point x^(q) ∈ Ω.

Then, we have to find P such that

Let us look for P within a space of admissible solutions. Generally, the task (8) cannot be exactly satisfied by any . So, let us accomplish this task as well as possible by solving the nonlinear constrained optimization problem

where the objective function is the root mean square (RMS) error in the accomplishment of the task (8).

Application to a heat concentration and cloaking problem

Let us apply the proposed optimization-based approach to design a device for heat concentration as alternative to that designed by Chen and Lei¹¹ based on transformation thermodynamics. This device, embedded in a plate with prescribed heat flux, is designed to concentrate the thermal energy at its center while keeping the outer flux unaltered (i.e., cloaking the device).

The Ω domain is the entire plate, a square of sides L_x = L_y = 14 cm subject to the following boundary conditions: T = T_max = 100 °C for x = −L_x/2, T = T_min = 0 °C for x = L_x/2, and q ⋅ n = 0 for y = ±L_y/2 (see Fig. 3). The heat flux normal to the plate is neglected. The plate is made of 40%-nickel steel with homogeneous and isotropic thermal conductivity k_ns = 10 W/(mK). Without the device, the heat flux in the plate is

Figure 3

Domain of analysis for the heat concentration and cloaking problem.

The considered device is the ring Ω_free ⊂ Ω with inner and outer radii r = 1 cm and R = 5 cm, see Fig. 3. This ring is designed to thermally concentrate the heat flux in the region Ω_fixint. A further design requirement on the device is to keep the heat flux outside it (i.e., in the remainder portion of the plate, Ω_fixext) unaltered.

The domain Ω is discretized using a mesh of 70 × 70 bilinear rectangular finite elements, as shown in Fig. 4(a). Each blue element, belonging to the device Ω_free, has a microstructure sampling point. In the other elements, the material is nickel steel.

Figure 4

(a) Finite element mesh of the analyzed domain Ω; the blue elements belong to the device, and the red ones have prescribed heat flux. (b) Representative volume element (RVE) of the microstructure at a point x^(μ) in the the heat flux manipulating device Ω_free.

Regarding the mesh refinement, it is well known that it affects the optimal result, as it is widely discussed in the book of Bendsøe and Sigmund¹³. Normally, the finer the mesh, the more optimal the solution. The current choice was found to be a good deal between optimality and computational cost.

Definition of the metamaterial for anisotropic heat conduction

Following Narayana and Sato², the anisotropy in the effective conductivity of the device Ω_free is achieved by using a stacked composite or laminate made of alternating sheets of materials A and B with different isotropic conductivities. As pointed out by Schittny et al.¹⁴, a laminate is a metamaterial because its effective conductivity, being anisotropic, goes beyond the conductivities of its constituents, which are isotropic.

Like Chen and Lei¹¹, we adopted A = copper and B = polydimethylsiloxane (PDMS), with isotropic conductivities k_copper = 398 W/(mK) and k_PDMS = 0.27 W/(mK). The use of laminates of materials with markedly distinct conductivity at the microstructural level leads to a highly anisotropic effective conductivity, which is a key issue for guiding the heat flux. Actually, it is a popular choice in the literature^2,11,15,16.

As shown in Fig. 4(b), the representative volume element (RVE) of the microstructure of such composite at the sampling point x^(μ) ∈ Ω_free is a unit square characterized by the vector p^(μ) of components (thickness of sheet of material A) and (orientation of the sheets); the thickness of the sheet of material B is d_B = l_μ − d_A, where l_μ = 1 is the thickness of the RVE. The effective thermal conductivities at x^(μ) in the direction of the sheets (λ) and normal to the sheets (τ) are¹⁷

These are principal conductivities, to be arranged in the matrix

Now, the matrix of tensorial components of the effective conductivity referred to the fixed Cartesian frame x-y at the point x^(μ) can be computed as

where R is the rotation matrix

The equation (10) explicitly defines the effective conductivity at a point as a function of the microstructure at that point.

Optimization settings

To design the current device implies to solve the optimization problem given by equation (9). The cloaking task is prescribed by setting at the center of the elements in Ω⁽¹⁾ and Ω⁽²⁾, while the heat concentration task is forced by setting at the center of elements in Ω_fixint, with R/r = 5 in this case. Note that the vector P contains as variables only the vectors p^(μ) characterizing the microstructure at the N = 1896 elements of Ω_free, with and , μ = 1, 2, … N.

For the chosen metamaterial, the current optimization problem is subject to the following box constraints:

Here, this nonlinear constrained optimization problem was solved using the IPOPT interior point algorithm¹⁸. Additional constraints may serve to avoid “complications”¹³: dependence on the finite element mesh, numerical instabilities, non-uniqueness of the solution, presence of multiple minima, etc. For the purpose of the current work, only the above box constraints are considered.

Results

The optimal solutions for d_A (that is in fact the fraction of copper since the RVE was assumed to be a unit square) and θ (the orientation of the sheets) in the device are plotted in Fig. 5, together with the corresponding temperature distribution. Note that the device accomplished the combined task up to an RMS error equal to = 1.67 kW/m² = 0.23||q₀||.

Figure 5

Optimal solutions without density filtering for the distribution of the fraction of copper (d_A), the orientation of copper and PDMS sheets (θ), and the temperature T in the concentrator device.

Although we considered this error to be small enough, the solution is seriously affected by “checkerboard”-type instabilities, mainly in the orientation field (Fig. 5 at the center). This is a well-known and widely studied defect in material distribution problems (see the book of Bendsøe and Sigmund¹³ and references therein), which can be avoided using the density filter technique proposed by Sigmund¹⁹. The components of the vector P are still the design variables for the optimization problem (8), but the objective function in equation (9) as well as the constraints (11) and (12) are evaluated for the vector of physical or filtered parameters . Then, the microstructure at the finite element e in Ω_free is actually characterized by the vector , which is defined as

where is the filter radius (to be adopted), measured from the center of the finite element e, p⁽ⁱ⁾ is the vector of design variables associated to the finite element i, Δ_ei is the distance between the centers of the elements e and i, and 〈x〉 is the ramp function (〈x〉 = x for x > 0, and 〈x〉 = 0 for x ≤ 0).

Now, solving the optimization problem (9) using density filtering with (i.e., five times the finite element size), we obtain the metamaterial distribution shown in Fig. 6, which is completely checkerboard-free. The so-obtained device Ω_free has a crosslike structure, with horizontal arms (parallel to q₀) mostly made of highly-conductive copper and vertical arms (normal to q₀) mostly made of poorly-conductive PDMS.

Figure 6

Optimal solutions using density filtering for the distribution of the fraction of copper (d_A), the fraction of PDMS (d_B), and the orientation of copper and PDMS sheets in the concentrator device.

As consequence of the metamaterial distribution depicted in Fig. 6, the effective thermal conductivity varies inside the device as shown in Fig. 7, being generally anisotropic. Thanks to this conductivity distribution in the device, the temperature field in the whole plate is that shown in Fig. 8(a). There, it can be qualitatively realized how well the given combined cloaking and concentration task was accomplished: First, isotherms are almost parallel and equally spaced outside the device, as it would be the case without the device. Secondly, inside the device, the isotherms are significantly bent towards the inner region (Ω_fixint), clearly demonstrating the strong energy concentration. This could be quantitatively appreciated in Fig. 8(b): The temperature along the center line y = 0, that where the heat flux is the most altered by the device, is slightly modified outside the device, while it has a gradient 4.58 times greater than the original one in the center of the device. Let us remark that, as solution of the optimization problem, the combined cloaking and concentration task was accomplished up to an RMS error equal to 2.04 kW/m² = 0.29 ||q₀||; individually, the RMS error for the concentration task in Ω_fixint was 3.34 kW/m² = 0.09 (R/r)||q₀||, while the RMS error for the cloaking task in Ω⁽¹⁾ and Ω⁽²⁾ was equal to 0.39 kW/m² = 0.05 ||q₀||. Although the minimization problem (9) accounts only for the portions Ω⁽¹⁾ and Ω⁽²⁾ of Ω_fixext, the heat flux is practically unaltered all around Ω_fixext: it approaches q₀ with a RMS error equal to 0.07 ||q₀||.

Figure 7

Distribution of the Cartesian components of the effective thermal conductivity in the concentrator device, given in W/(mK).

Figure 8

(a) Temperature distribution in the plate, in °C; the difference between isotherms is 2 °C. (b) Temperature profile along (a–d).

Chen and Lei¹¹ defined a concentration efficiency index as f = |(T_b − T_c)/(T_a − T_d)|, where b and c are points located in the boundary of the heat concentration region Ω_fixint, and a and d are points located at the outer boundary of the device Ω_free (see Fig. 8(b)). For the current device, we obtain f = 94.2%, close to the ideal f = 100%. Let us recall that the device designed by Chen and Lei based on the transformation approach, made of 100 radial copper-PDMS laminates, had a theoretical efficiency f = 96.3%, which fell to f = 88.1% for the finally fabricated device.

Comparing the current device to Chen and Lei’s one, it appears a crucial advantage of the current optimization-based design with respect to the transformation-based design: the device is designed just for the desired task (to manipulate an originally one-direction heat flux), avoiding to “oversize” it by performing unwanted or unprescribed tasks (in the case of Chen and Lei’s device, to manipulate the heat flux coming from any direction). Further, if the task is only to concentrate heat, the cloaking task is just a collateral result of applying the transformation-based approach.

Note that the current device can be seen as a neutral inclusion because of its cloaking effect. A priori, according to the theory of neutral inclusions (see chapter 7 in the book of Milton²⁰ and references therein), it would be possible to determine in an analytical way a homogeneous isotropic material to make the cloaking device, a solution that is considerably more convenient than the current one using a heterogeneous metamaterial. However, let us remark that this trivial solution is not applicable to the current case. Actually, applying the Hashin-Shtrikman formula²¹ with the regions outside and enclosed by the device having the same isotropic conductivity k_ns, we determine that the only way of keeping the exterior flux unaltered is choosing the isotropic conductivity inside the device also equal to k_ns, which leads to completely ignore the heat flux concentration task.

Conclusions

We presented a novel method for designing metamaterials to control the diffusive heat flux in ways that were inconceivable using ordinary materials. This method consists in solving an optimization problem where the objective function to be minimized is the error in the accomplishment of a given heat flux control task, and the design variables define the microstructure in a heat flux manipulating device. Its potentiality was proved by designing a device for energy concentration that has close-to-ideal efficiency and, at the same time, leaves the external heat flux practically unaltered.

We expect these results may create opportunities to develop new advanced engineered materials for enhancing the efficiency of thermal devices in solar thermal collectors, for instance.

Future work will be devoted to ensure the manufacturability of these optimization-based designs.