Entanglement and nonclassicality in four-mode Gaussian states generated via parametric down-conversion and frequency up-conversion

Abstract

Multipartite entanglement and nonclassicality of four-mode Gaussian states generated in two simultaneous nonlinear processes involving parametric down-conversion and frequency up-conversion are analyzed assuming the vacuum as the initial state. Suitable conditions for the generation of highly entangled states are found. Transfer of the entanglement from the down-converted modes into the up-converted ones is also suggested. The analysis of the whole set of states reveals that sub-shot-noise intensity correlations between the equally-populated down-converted modes, as well as the equally-populated up-converted modes, uniquely identify entangled states. They represent a powerful entanglement identifier also in other cases with arbitrarily populated modes.

Introduction

Since the discovery of quantum mechanics, entanglement has been considered a very peculiar and purely quantum feature of the physical systems. Its fundamental importance emerged when the experiments showing the violation of the Bell inequalities^1,2,3, implementing quantum teleportation^4,5 or demonstrating dense coding were performed. Nowadays, entanglement is undoubtedly considered as the key resource of modern and emerging quantum technology, including quantum metrology, quantum computation⁶ and quantum communications^7,8,9.

For this reason, a great deal of attention has been devoted to the construction of practical sources of entangled light, both in the domains of discrete and continuous variables. While individual entangled photon pairs arising in spontaneous parametric down-conversion are commonly used in the discrete domain¹⁰, single-mode as well as two-mode squeezed states originating in parametric down-conversion and containing many photon pairs represent the sources in the domain of continuous variables¹¹. Even more complex nonlinear optical processes, including those combining simultaneous parametric down-conversion and frequency up-conversion, have been analyzed as sources of more complex entangled states. This approach has been experimentally implemented in refs 12 and 13 considering three-mode entanglement and in ref. 14 where the four-mode entanglement has been analyzed.

Here, we consider a four-mode system composed of two down-converted modes and two up-converted modes. In the system, parametric down-conversion and frequency up-conversion involving both down-converted modes simultaneously occur in the same nonlinear medium¹⁵. While parametric down-conversion serves as the primary source of entanglement¹⁶, frequency up-conversion is responsible for the transfer of the entanglement to the up-converted modes.

This transfer operation is interesting from the fundamental point of view, as it generalizes the well-known property of ‘one-mode’ frequency up-conversion pumped by a strong coherent field, in which the statistical properties of the incident field are transferred to the frequency up-converted counterpart, also including the nonclassical ones (for example, squeezing,¹⁷). We note that such properties are important for the applications of the up-conversion process: For instance, it has been used many times for ‘shifting’ an optical ‘one-mode’ field to an appropriate frequency where its detection could be easily achieved^18,19.

In the general analysis of the four-mode system, we quantify its global nonclassicality via the Lee nonclassicality depth²⁰. Since the four-mode system under consideration cannot exhibit nonclassicality of individual single modes, the global nonclassicality automatically implies the presence of entanglement among the modes for a two-mode Gaussian system involving parametric down-conversion, (see ref. 21). The analysis of ‘the structure of entanglement’ further simplifies by applying the Van Loock and Furusawa inseparability criterion²² that excludes the presence of genuine three- and four-partite entangled states. This means that in the system discussed here there are only bipartite entangled states. It is thus sufficient to divide the analyzed four-mode state into different bipartitions to monitor the structure of entanglement. Then, the well-known entanglement criterion based on the positive partial transposition of the statistical operator^23,24, which gives the logarithmic negativity as an entanglement quantifier, is straightforwardly applied^25,26.

The experimental detection of two-mode (-partite) entanglement is in general quite challenging, as it requires measurements in complementary bases. Here, we theoretically show that, for the considered system with the assumed initial vacuum state, any two-mode partition exhibiting sub-shot-noise intensity correlations is also entangled. As a consequence, the measurement of intensity auto- and cross-correlations in this system is sufficient to give the evidence of the presence of two-mode entangled states through the commonly used noise reduction factor.

Finally, we note that the Hamiltonian of the analyzed four-mode system formally resembles that describing a twin beam with signal and idler fields divided at two beam splitters. This analogy results in similar properties of the four-mode states obtained in the two cases, though the processes of down-conversion and up-conversion occur simultaneously in our system, at variance with the system with two beam splitters, which modify the already emitted twin beam. We note that the system with two beam splitters has been frequently addressed in the literature as a prototype of more complex devices based on two multiports that are used to have access to intensity correlation functions for the detailed characterization of the measured fields²⁷, also including their photon-number statistics^{28,29,30,31,32,33}.

The paper is organized as follows. In Section Four-mode nonlinear interaction the model of four-mode nonlinear interaction including parametric down-conversion and frequency up-conversion is analyzed. Nonclassicality of the overall system is addressed in Section Nonclassicality. In Section Four-mode entanglement, the entanglement of the overall system is investigated considering the partitioning of the state into different bipartitions. Two-mode entangled states obtained after state reduction are analyzed in Section Two-mode entanglement and noise reduction factor, together with two-mode sub-shot-noise intensity correlations. Suitable parameters of the corresponding experimental setup can be found in Section Experimental implementation. Section Conclusions summarizes the obtained results.

Four-mode nonlinear interaction

We consider a system of four nonlinearly interacting optical modes (for the scheme, see Fig. 1). Photons in modes 1 and 2 are generated by parametric down-conversion with strong pumping (coupling constant g₁). Photons in mode 1 (2) can then be annihilated with the simultaneous creation of photons in mode 3 (4). The two up-conversion processes are possible thanks to the presence of two additional strong pump fields with coupling constants g₂ and g₃. The overall interaction Hamiltonian for the considered four-mode system is written as¹⁵:

Figure 1: Optical fields in modes 1 and 2 interact via parametric down-conversion described by the nonlinear coupling constant g₁.

Photons from mode 1 (2) are converted into photons of mode 3 (4) thanks to the frequency up-conversion characterized by the coupling constant g₂ (g₃); t stands for the interaction time. In the symmetric case we have g₂₃ = g₂ = g₃.

where the operators and create an entangled photon pair in modes 1 and 2 and the creation operators and put the up-converted photons into modes 3 and 4, respectively. Symbol H.c. replaces the Hermitian conjugated terms.

The Heisenberg-Langevin equations corresponding to the Hamiltonian in Eq. (1) are written in their matrix form as follows:

where and . The matrix U introduced in Eq. (2) is expressed as

in which γ_j stands for the damping coefficient of mode j, j = 1, …, 4. The Langevin operators , j = 1, …, 4, obey the following relations:

The Kronecker symbol is denoted as δ_ij and the symbol δ(t) means the Dirac function. The mean numbers n_dj corresponding to noise reservoir photons have been used in Eq. (4). We note that for the noiseless system the following quantity is conserved in the interaction.

Introducing frequencies ω_j and wave vectors of the mutually interacting modes, we formulate the assumed ideal frequency and phase-matching conditions of the considered nonlinear interactions in the form:

In Eq. (5), ω_p12 () stands for the pump-field frequency (wave vector) of parametric down-conversion, whereas ω_p13 [ω_p24] []) means the frequency (wave vector) of the field pumping the up-conversion process between modes 1 [2] and 3 [4].

The solution of the system of first-order linear operator stochastic equations (2) can be conveniently expressed in the following matrix form:

where the evolution matrix M is written in Eq. (18) of Appendix for the noiseless case and vector arises from the presence of the stochastic Langevin forces. More details can be found in ref. 34. When applying the solution (6), we consider the appropriate phases of the three pump fields such that the coupling constants g_j, j = 1, 2, 3, are real.

The statistical properties of the optical fields generated both by parametric down-conversion and up-conversion are described by the normal characteristic function defined as

where Tr denotes the trace and β ≡ (β₁, β₂, β₃, β₄)^T. Using the solution given in Eq. (6), the normal characteristic function attains the Gaussian form:

and c.c. replaces the complex conjugated terms. The coefficients occurring in Eq. (8) are derived in the form:

We note that the two-mode interactions characterized by the coefficients D_ij and in Eq. (8) attain specific forms. While the coefficients D_ij reflect the presence of photon pairs in modes i and j, coefficients describe mutual transfer of individual photons between modes i and j.

The normal characteristic function can be rewritten in the matrix form exp(β^†A β/2) by introducing the normally-ordered covariance matrix A:

where the 2 × 2 matrices are defined as:

The covariance matrix σ related to the symmetric ordering and corresponding to the phase space is needed to perform easily partial transposition. It has the same structure as the covariance matrix A written in Eq. (10) with the blocks A_i (D_jk) replaced by the blocks σ_i (ε_jk) defined as:

Symbol Re (Im) denotes the real (imaginary) part of the argument.

In what follows, we consider the situation in which all four modes begin their interaction in the vacuum state. Moreover, we focus on the specific symmetric case in which g₂ = g₃ ≡ g₂₃. A note concerning the general case g₂ ≠ g₃ is found at the end.

Nonclassicality

We first analyze the global nonclassicality of the whole four-mode system as it is relatively easy and, for the considered initial vacuum state, it implies entanglement (see below). Nonclassicality of the whole four-mode state described by the statistical operator is conveniently quantified by the Lee nonclassicality depth τ²⁰. This quantity gives the amount of noise, expressed in photon numbers, needed to conceal nonclassical properties exhibited by the Glauber-Sudarshan P function, which attains negative values in certain regions or even does not exist as an ordinary function. The Glauber-Sudarshan P function is determined by the Fourier transform of the normally-ordered characteristic function given in Eq. (8). Technically, the Lee nonclassicality depth is given by the largest positive eigenvalue of the covariance matrix A defined in Eq. (10). So, it can be easily determined.

The Lee nonclassicality depth τ as a function of the coupling parameters g₁t and g₂₃t is shown in Fig. 2. The increasing values of g₁t result in larger values of the nonclassicality depth τ, as the number of photons simultaneously generated in modes 1 and 2 increases. We note that this pairing of photons in the process of parametric down-conversion is the only source of nonclassicality in the analyzed four-mode system. On the contrary, nonzero values of parameter g₂₃t only lead to the oscillations of the nonclassicality depth τ. This behavior occurs as the frequency up-conversion moves photons, and so also photon pairs, from modes 1 and 2 to modes 3 and 4 and vice versa (see the scheme in Fig. 1). This results in the nonclassical properties of modes 3 and 4, at the expenses of the nonclassical properties of modes 1 and 2.

Figure 2

Nonclassicality depth τ as a function of the parameters g₁t and g₂₃t.

The maximum value of the Lee nonclassicality depth τ = 0.5 is reached for g₂₃t = 0 and ideally in the limit g₁t → ∞, i.e. when only the strong parametric down-conversion occurs. This is in agreement with the analysis of nonclassical properties of twin beams reported in ref. 35. The value τ = 0.5 can also be asymptotically reached in the limit g₂₃t → ∞, in which we have

with B₃ → B₁, B₄ → B₂ and D₃₄ → D₁₂. It is worth noting that formula (13) applies also for g₂₃t = 0.

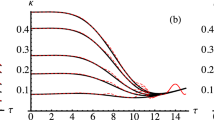
Nonclassicality is also strongly resistant against damping in the system. This means that even a low number of photon pairs is sufficient to have a nonclassical state. We demonstrate this resistance by considering the damping constants γ proportional to the nonlinear coupling constant g₁, which quantifies the speed of photon-pair generation. The graphs in Fig. 3 show that the generated states remain strongly nonclassical even though a considerable fraction of photon pairs is broken under these conditions. The comparison of graphs in Fig. 3(a,b) reveals that the damping is more detrimental in the down-converted modes 1 and 2 than in the up-converted modes 3 and 4.

Figure 3

Nonclassicality depth τ as a function of the parameters g₁t and g₂₃t for (a) γ₁t = γ₂t = g₁t, γ₃t = γ₄t = 0; (b) γ₁t = γ₂t = 0, γ₃t = γ₄t = g₁t, assuming n_dj = 0 for j = 1, …, 4.

At variance with nonclassicality, the determination and quantification of entanglement is more complex and it is technically accomplished by considering all possible bipartitions of the four-mode system (see the next Section). On the one side all bipartitions considered below are in principle sufficient to indicate entanglement, on the other side the application of the Van Loock and Furusawa inseparability criterion²² to our system excludes the presence of genuine three- and four-mode entanglement. The analyzed Hamiltonian written in Eq. (1) together with the incident vacuum state also excludes the presence of nonclassical states in individual modes. In what follows, the bipartite entanglement is thus the only source of the global nonclassicality in the analyzed system. This situation considerably simplifies the possible experimental investigations as positive values of the Lee nonclassicality depth directly imply the presence of entanglement somewhere in the system.

Four-mode entanglement

In quantifying the entanglement in our four-mode Gaussian system, we rely on the following facts applicable to an arbitrary (m + n)-mode Gaussian state. It has been proven that positivity of the partially transposed (PPT) statistical operator describing any 2 × 2 or 2 × 3 bipartition of the state is a necessary condition for the separability of the state^23,24. Moreover, it has been shown that the violation of PPT condition occurring in any 1 × (m + n − 1) bipartitions or m × n bisymmetric bipartitions for m > 2 and n > 3 is a sufficient condition for the entanglement in the analyzed (m + n)-mode state^36,37. For continuous variables systems, the PPT is simply accomplished when the symmetrically-ordered field operators are considered allowing to perform the PPT only by changing the signs of the momenta ³⁶. Moreover, symplectic eiganvalues of the symmetrically-ordered covariance matrix σ can be conveniently used to quantify entanglement in bipartite systems via the logarithmic negativity E²⁶, defined in terms of eigenvalues :

where max gives the maximal value.

In the four-mode Gaussian state sketched in Fig. 1, we have two kinds of bipartitions. Either a single mode forms one subsystem and the remaining three modes belong to the other subsystem, or two modes are in one subsystem and the remaining two modes lie in the other subsystem. Due to the symmetry, only two members of each group are of interest for us. Namely, these are bipartitions 1 × 234 and 3 × 124 from the first group and bipartitions 12 × 34 and 13 × 24 from the second one. We note that, while the bipartition 12 × 34 is bisymmetric in our interaction configuration (provided that g₂t = g₃t), the bipartition 13 × 24 is not bisymmetric. Nevertheless, positive values of both the logarithmic negativities E_12×34 and E_13×24 reflect entanglement as both bipartitions involve two modes on both sides. Similarly, positive values of the logarithmic negativities E_1×234 and E_3×124 guarantee the presence of entanglement.

We first pay attention to the entanglement expressed in the logarithmic negativities E_1×234 and E_3×124. As suggested by the graphs in Fig. 4(a,b), the oscillating behavior of negativity E_1×234 is complementary to that of negativity E_3×124. This means that the larger values of negativity E_1×234 are accompanied by the lower values of negativity E_3×124 and vice versa. Such a result is a consequence of the fact that the entanglement is due to the presence of photon pairs and a photon created in mode 1 can move to mode 3 and later return back to mode 1. This movement leads to the oscillations with frequency g₂₃, which are clearly visible in Fig. 4(a,b). This explanation also suggests that no entanglement is possible between modes 1 and 3. Indeed, if we also determine the negativity E_1×24 (or E_3×24), we will get the same values already obtained for the negativity E_1×234 (E_3×124).

Figure 4

Logarithmic negativities E_1×234 (a), E_3×124 (b), E_12×34 (c), and E_13×24 (d) as functions of parameters g₁t and g₂₃t for different bipartitions indicated in the subscripts.

The negativity E_12×34, characterizing the entanglement between the twin beam in modes 1 and 2 and the up-converted beams in modes 3 and 4, is plotted in Fig. 4(c). It reflects the gradual movement of photon pairs from modes 1 and 2, where they are created, to modes 3 and 4. Note that the maxima of negativity E_12×34 along the g₂₃t-axis occur inbetween the maxima of negativities E_1×234 and E_3×124. The origin of entanglement in photon pairing is confirmed in the graph of Fig. 4(d), showing that the negativity E_13×24 is independent of parameter g₂₃t and that the negativity E_13×24 increases with the increasing parameter g₁t. In certain sense, the independence of negativity E_13×24 from parameter g₂₃t represents the conservation law for nonclassical resources, as the negativities of the different two-mode reductions derived from this bipartition (E_1×2, E_1×4, E_3×2, and E_3×4) do depend on parameter g₂₃t.

The developed model also allows us to study the role of damping in the entanglement creation. The investigations based on equal damping constants γ and noiseless reservoirs (n_d = 0) just reveal the deterioration of entanglement in all the considered bipartitions with the increase of damping constants see (Fig. 5).

Figure 5: Logarithmic negativity E as a function of the damping coefficient γt for different bipartitions: 1 × 234 (dashed red line), 3 × 124 (brown dotted line), 12 × 34 (dashed-dotted green line), and 13 × 24 (solid blue line).

We set g₁t = g₂t = g₃t = 0.7, γ ≡ γ₁ = γ₂ = γ₃ = γ₄; n_dj = 0 for j = 1, …, 4.

Two-mode entanglement and noise reduction factor

The results of the theoretical analysis suggest that, from the experimental point of view, the observation of entanglement between pairs of modes is substantial for the characterization of the emitted entangled states. Formally, the theory describes such observations through the reduced two-mode statistical operators. The analysis shows that the behavior of two-mode negativities E_1×2, E_3×4, and E_1×4 with respect to parameters g₁t and g₂₃t is qualitatively similar to that of four-mode negativities E_1×234, E_3×124, and E_12×34 plotted in Fig. 4(a–c). This similarity originates in possible ‘trajectories’ of photon pairs born in modes 1 and 2 and responsible for the entanglement.

Additional insight into the generation of entanglement in the analyzed system is provided when the entanglement is related to the intensities of the interacting fields. As quantified in the graphs of Fig. 6, both mean photon numbers B₁ ≡ B₂ and B₃ ≡ B₄ are increasing functions of parameter g₁t and oscillating functions of parameter g₂₃t. This oscillating behavior is particularly interesting, as it reflects the flow of photons from modes 1 and 2 to modes 3 and 4, respectively, and vice versa. As we will see below, this is in agreement with the ‘flow of the entanglement’ among the modes.

Figure 6

Mean photon numbers B₁ (a) and B₃ (b) plotted as functions of parameters g₁t and g₂₃t.

The graph in Fig. 7(a) shows that the negativity E_1×2 is on the one side an increasing function of the mean photon number B₁, on the other side it only weakly depends on the mean photon number B₃. This confirms that pairing of photons in parametric down-conversion is the only resource for entanglement creation. On the contrary, as shown in Fig. 7(b), the negativity E_3×4 is an increasing function of the mean photon number B₃, whereas it weakly depends on the mean photon number B₁. This indicates that the entanglement in modes 34 comes from modes 12 through the transfer of photon pairs: The stronger the transfer is, the larger the value of negativity E_3×4 is. Moreover, optimal conditions for the observation of entanglement in modes 1 and 4 occur provided that there is the largest available number of photon pairs with one photon in mode 1 and its twin in mode 4. According to the graph in Fig. 7(c) this occurs when the mean photon numbers B₄ (B₄ ≡ B₃) and B₁ are balanced, independently of their values.

Figure 7

Logarithmic negativities E_1×2 (a), E_3×4 (b) and E_1×4 (c) as functions of the mean photon numbers B₁ and B₃.

In general, the experimental identification of two-mode entanglement is not easy, as it requires the simultaneous measurement of the entangled state in two complementary bases. Alternatively, entanglement can be inferred from the reconstructed two-mode phase-space quasi-distribution, which needs two simultaneous homodyne detectors³⁸, each one endowed with a local oscillator. However, the detection of entanglement, at least in some cases, can be experimentally accomplished by the observation of sub-shot-noise intensity correlations. This is a consequence of the detailed numerical analysis, which reveals that the majority of the reduced two-mode entangled states also exhibits sub-shot-noise intensity correlations. Nevertheless, it should be emphasized here that, in the analyzed system, there are also two-mode entangled states not exhibiting sub-shot-noise intensity correlations. On the contrary, we note that the reduced two-mode separable states do not naturally exhibit sub-shot-noise intensity correlations.

Sub-shot-noise intensity correlations are quantified by the noise reduction factor R^39,40, that is routinely measured to recognize nonclassical intensity correlations of two optical fields. The noise reduction factor R expressed in the moments of photon numbers n_j and n_k of modes j and k, respectively, is defined by the formula:

Sub-shot-noise intensity correlations are described by the condition R < 1. We note that there exists the whole hierarchy of inequalities involving higher-order moments of photon numbers (or intensities)^27,33,41,42 that indicate nonclassicality and, in our system, also entanglement. We mention here the inequality derived by Lee⁴³ as a practical example that is sometimes used in the experimental identification of nonclassicality. We note that this criterion is stronger than the noise reduction factor R in revealing the nonclassicality³⁹.

The noise reduction factors R_1×2, R_3×4 and R_1×4 describing the reduced two-mode fields with their negativities plotted in Fig. 7 are drawn in Fig. 8 for comparison. We can see complementary behavior of the negativities E and noise reduction factors R in the graphs in Figs 7 and 8. An increase of the negativity E is accompanied by a decrease in the noise reduction factor R. A closer inspection of the curves in these graphs shows that the condition R < 1 identifies very well entangled states when the noise reduction factor is measured in modes 1 × 2 and 3 × 4. Nevertheless, there are entangled states with R_1×4 > 1, as shown in the graph of Fig. 9, in which the values of parameters g₁t and g₂₃t appropriate for this situation occur in the areas I and III. On the other hand, the entangled states found in the area II in the graph of Fig. 9 have R < 1. It is worth noting that the relative amount of entangled states not detected via R < 1 increases with the increasing coupling constant g₁t and so with the increasing overall number of photons in the system.

Figure 8

Noise reduction factors R_1×2 (a), R_3×4 (b) and R_1×4 (c) as functions of the mean photon numbers B₁ and B₃. In (c), the plane defined as R_1×4 = 1 is represented by the blue mesh.

Figure 9: Solutions of the equations for logarithmic negativity E_1×4 = 0 (blue dashed line) and noise reduction factor R_1×4 = 1 (red solid line) in the plane spanned by parameters g₁t and g₂₃t.

The two-mode field is entangled (E_1×4 > 0) inbetween the blue dashed lines, i.e. in the areas I, II, and III, whereas it is sub-shot-noise (R_1×4 < 1) in between the red solid lines, i.e. in the area II.

The observed relation between the entangled states and those exhibiting sub-shot-noise intensity correlations can even be explained theoretically, due to the specific form of the reduced two-mode Gaussian states analyzed in ref. 35. According to ref. 35 entangled states in modes i and j are identified through the inequality B_iB_j < |D_ij|². On the other hand, the noise reduction factor R_ij defined in Eq. (15) attains for our modes the form:

that assigns the sub-shot-noise intensity correlations to the states obeying the inequality . Thus, the inequality implies that the states with sub-shot-noise intensity correlations form a subset in the set of all entangled states. Moreover, if B_i = B_j, both sets coincide as we have . Thus, the noise reduction factors R₁₂ and R₃₄ are reliable in identifying entangled states in the symmetric case, in which B₁ = B₂ and B₃ = B₄.

We note that, according to the theory developed for the modes without an additional internal structure³⁵, the logarithmic negativity E_ij can be determined along the formula³⁵

where |D_ij|² = 〈Δn_iΔn_j〉. According to Eq. 17 the logarithmic negativity E_ij can, in principle, be inferred from the measured mean intensities in modes i and j and the cross-correlation function of intensity fluctuations in this idealized case.

At the end, we make a note about the entanglement in the general four-mode system with different up-conversion coupling constants (g₂ ≠ g₃). This is relevant when non-ideal phase-matching conditions of the three nonlinear interactions are met in the experiment (see below). According to our investigations, the largest values of negativities E_1×2 and E_3×4 are found in the symmetric four-mode system (g₂ = g₃) considered above. On the contrary, the largest values of negativities E_1×4 and E_2×3 are obtained for unbalanced g₂ and g₃ interactions.

Similarly to the symmetric case, separable states, entangled states without sub-shot-noise intensity correlations and entangled states exhibiting sub-shot-noise intensity correlations are found in the whole three-dimensional parametric space spanned by variables g_jt for j = 1, 2, 3. As an example, the distribution of different kinds of reduced two-mode states found in the up-converted modes 3 and 4 in this space is plotted in Fig. 10. The graphs in Fig. 10 indicate that, in accord with the symmetric case, the larger the value of constant g₁t, the larger the relative amount of entangled states that cannot be identified through sub-shot-noise intensity correlations.

Figure 10

Planes given by g₁t = 0.5 (a), g₁t = 1 (b) and g₁t = 5 (c) in the ‘phase diagram’ identifying classical states (white areas), entangled states without sub-shot-noise intensity correlations (blue) and entangled states with sub-shot-noise intensity correlations (red) in the space spanned by the coupling constants g_jt, j = 1, 2, 3.

Experimental implementation

A possible experimental implementation of the four mode interaction described above can be achieved by using a BaB₂O₄ crystal as the nonlinear medium, a ps-pulsed laser (a mode-locked Nd:YLF laser regeneratively amplified at 500 Hz, High-Q Laser Production) to get the pump fields and hybrid photodetectors (mod. R10467U-40, Hamamatsu Photonics) as the photon-number-resolving detectors. A typical experimental setup can be built in analogy with other previous experiments³³. The phase-matching conditions can be chosen so as to have ω₁ = ω₂ and a common pump field for both up-conversion processes so that ω₃ = ω₄. In this specific symmetric case we have g₂ = g₃ ≡ g₂₃.

We can estimate the range of coupling constants achievable in this setup based on the above-mentioned laser source. Let us consider the following parameters: wavelength of the pump for down-conversion λ_p1 = 349 nm, λ₁ = λ₂ = 698 nm, wavelength of the pump for up-conversion λ_p2 = 1047 nm, λ₃ = λ₄ = 418.8 nm, length of the BaB₂O₄ crystal L = 4 mm, diameters of the pumps 0.5 mm, pulse duration 4.5 ps. The coupling constants g₁ and g₂₃ are linearly proportional to the corresponding pump field amplitudes so that g₁t = κ₁A_p1L and g₂₃t = κ₂₃A_p2L, where κ_j (j = 1, 23) are the nonlinear coupling coefficients and A_j (j = p1, p2) are the pump amplitudes. For the considered parameters we can estimate κ_j ≈ 10⁻¹³s^1/2. The useful range of energies per pulse is up to 66 μJ in the UV and up to 240 μJ in the IR, corresponding to maximum values g₁t ≈ 5.9 and g₂t ≈ 7. The theoretical results discussed above predict an interesting behavior for this range of parameters, including the transfer of entanglement into the up-converted modes.

Conclusions

Four-mode Gaussian states generated via parametric down-conversion and frequency up-conversion have been analyzed in terms of nonclassicality, entanglement and entanglement transfer among the modes. While nonclassicality of the state has been described by the easily-computable Lee nonclassicality depth, logarithmic negativity for different bipartitions has been applied to monitor the occurrence of entanglement among different modes. It has been shown that whenever the analyzed system is nonclassical, it is also entangled. Moreover, the entanglement is present only in the form of bipartite entanglement. The analysis of the noise reduction factor identifying sub-shot-noise intensity correlations, in parallel with the logarithmic negativity quantifying two-mode entanglement, has shown that the noise reduction factor is a powerful indicator of the entanglement in the analyzed system. This is substantial for the experimental demonstration of the transfer of entanglement from the down-converted modes to the up-converted ones.

The evolution matrix M

The evolution matrix M describing the operator solution of the Heisenberg equations written in Eq. (2) is derived in the form:

where x = (a + b)/2, x₁ = (a₁ + b)/2, y = (a − b)/2, y₁ = (a₁ − b)/2, , , , , , , and .