Introduction

It is well known that scalar optical vortices having a spatially distributed skew phase front exp(iφ) have an orbital angular momentum (OAM) of ħ per photon, where is topological charge1. Light-carrying OAM has some practical applications, such as optical communication2 and remote sensing3. Additionally, if the states of polarization (SOP) of light are space-variant, vectorial vortex beams (VVBs) with polarization singularities appear. A polarization singularity occurs around a point where a scalar vortex is centered in one of the scalar component of VVBs4. One interesting property of VVBs is that they can have OAM if a Pancharatnam phase is embedded on the beam5. The Pancharatnam phase, also called the Pancharatnam–Berry geometrical phase, usually occurs in the polarization manipulation of ligh6,7. Some optical devices such as q-plates8 or subwavelength elements9 based on the Pancharatnam–Berry phase can generate VVBs with the Pancharatnam phase, leading to the carrying of OAM. Recently, the potential for use of VVBs in optical communication has been demonstrated experimentally10,11.

In principle, VVBs are constructed by superimposing two orthogonally polarized OAM eigenstates with different topological charges. Nowadays, various methods are employed to generate VVBs by using a liquid crystal spatial light modulator (SLM)12,13,14. However, most previous works on this topic discuss cases where the magnitudes of the two topological charges and weights of the two OAM eigenstates are equal14,15. Although experimental results pertaining to unequal topological charge magnitudes are available, the OAM of light has not been investigated adequately16. In this paper, we apply a similar technique as that proposed by Moreno et al.15,17 to study cases where both the topological charges and the weights of two OAM eigenstates are unequal. It is shown that using these degrees of freedom, independent control of polarization patterns and OAM charges of VVBs is possible. In addition, the generated VVBs with a Pancharatnam phase correspond to a coordinate on the hybrid-order Poincaré sphere18, which is proposed to describe the evolution of polarization states in inhomogeneous anisotropc media. In the experiment, the panel of a reflective SLM is divided into equal areas, and each of them displays a helical phase hologram to encode OAM eigenstates onto the x- and y-polarized components of incident light, respectively. Next, a quarter-wave plate (QWP) is used to transform the two linear polarization states into another pair of orthogonal polarization states; this step yields two orthogonally polarized OAM eigenstates that further span the VVB subspace. The weighting factors of the two eigenstates can be controlled by adjusting the polarization angle of the incident linearly polarized beam, while the topological charge of each eigenstate can be controlled independently by two separate halves of a single SLM. To evaluate the properties of the generated VVBs, we successively apply two measurement procedures. First, we use Stokes polarimetry8,19 to study the polarization patterns of the generated beams. Second, we use a Shack–Hartmann wavefront sensor to demonstrate the existence of OAM and further infer the actual OAM charge of beams20. Theoretical and experimental results pertaining to SOP and OAM charges are in good agreement.

Results

Theoretical description of vectorial vortex beams

The normalized Jones vector of a VVB propagating along the +z direction can be expressed as follows18,21

where (i = 1, 2) denotes one of orthogonally polarized OAM eigenstates with a topological charge of mi, φ is the azimuthal coordinate of the beam, and the weighting factors of each eigenstate are governed by two complex constants ci = |ci|. Field normalization requires that

For the benefit of the reader, we briefly outline the approach to constructing VVBs by using equation (1). For simplicity, we first consider a special case where = and = , that is, two orthogonal linear polarization eigenstates. By substituting equation (1) into the definition of Stokes parameters, we obtain

whereδ ≡ δ1 − δ2 is the phase difference between the two complex constants of ci, and it is related to the choice of origin of the azimuthal φ-coordinate. Equations (4)–(6), , imply that all SOP on the transverse plane can be described completely by a geodesic path with a radius of 2|c1||c2|, located on the plane of intersection of S1 = |c2|2 − |c1|2 with the Poincaré sphere, as shown in Fig. 1(a). Moreover, both S2 and S3 depend only on the value of (m1 − m2) and, therefore, SOP does, too. The fact of SOP depend only on (m1 − m2) can also be found in equation (1) because the sum of m1 and m2 is only relevant to the common phase factor of the two orthogonal eigenstates. To control SOP, one can adjust the coefficients of ci, which would result in shifting of the geodesic path on the sphere, or adjust the value of (m1 − m2). Figure 1(b–d) show the simulated results of the orientation angle (ψ) and the ellipticity angle (χ) of SOP for c1 = 0.5 and c2 = 0.87, but different values of (m1 − m2) = 1, −3, and 3. These results were obtained by substituting equations (4)–(6), , into equations (23) and (24), where the angle ψ (−π/2 ≤ ψ ≤ π/2) determines the direction of the major axis of the polarization ellipses, and χ (−π/4 ≤ χ ≤ π/4) determines the ratio of the minor to the major axes of the ellipses. In addition, χ is positive for right-handed polarizations (blue ellipses) but negative for left-handed (red ellipses). By comparing Fig. 1(b–d), it can be seen that the azimuthal gradient of SOP depends on the absolute value of (m1 − m2) while the distribution of handedness depends on its sign. Furthermore, the distribution of SOP depends only on the azimuthal angle of φ because there is only one spatial variable of φ in equation (1). Although we discuss only orthogonal linear polarization eigenstates, similar discussions can be applied to another pair of orthogonally polarized eigenstates. For detailed discussions, please refer to the supplementary information.

Figure 1: Illustration of using equation (1) to construct VVBs.
figure 1

(a) In this example, polarization eigenstates of in equation (1) are chosen as linearly polarized states, denoted by and , respectively. The two weighting coefficients are c1 = 0.5 and c2 = 0.87, respectively. The geodesic path (green line) marked on the Poincaré sphere describes the SOP on the transverse plane. (b–d) Simulation results of ellipticity and orientation angles of polarization ellipses. The blue and red ellipses on the color maps represent right- and left-handed polarizations, respectively.

Full size image

The average OAM charge in equation (1) can be found by examining the ratio of the z component of OAM to its energy over the transverse plane of light22. This is given as follows

where c is the speed of light in free space, ω is the angular frequency of light, jz is the z component of OAM density, pz is the z component of linear momentum density, and α and β are complex amplitudes of the x and y electric field components of the VVBs22. In fact, it is shown in the supplementary information that the average OAM charge in equation (1) is independent of the selection of polarization eigenstates of . As proved in the supplementary information, the average OAM charge is

One can also find the Pancharatnam phase φp in equation (1) from the following definition5,22,23

where is the reference field, and the operator “arg” denotes the argument of the inner product. By comparing equations (10) and (11), it can be found that if c1 = c2 and m1 = −m2, either the Pancharatnam phase or the OAM charge vanishes, while other opposite cases are true. From above discussions, we conclude that SOP depend on the value of (m1 − m2), as well as on the two selected orthogonal polarization eigenstates, whereas OAM charge depends not only on the weighting coefficients but also on the values of m1 and m2. Consequently, independent control of OAM charges and polarization patterns of VVBs can be achieved by manipulating various parameters. Details of the relationship between the OAM charge and the Pancharatnam phase can be found in the literature22.

Experimental setup

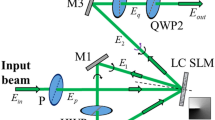
The double modulation scheme is shown in Fig. 2. A diode-pumped solid-state (DPSS) laser beam (Verdi, λ = 532 nm) is filtered and expanded by the first telescope consisting of lens L1 (f1 = 15 mm) and L2 (f2 = 150 mm) and then passes through a polarizer (P1) and an HWP. P1 is introduced to generate a linearly polarized beam, and the HWP is used to adjust the polarization plane of the linearly polarized beam. The beam with its polarization making an angle θ with the x-axis is then incident on the half panel of a phase-only reflective SLM (Holoeye Photomics, PLUTO-VIS, 1920 × 1080 pixels) with LC molecules aligned in the x direction. The extinction ratio of the SLM is about −18 dB. Two different helical phase holograms with 900 × 900 pixels are simultaneously displayed side by side onto the SLM to independently encode the x and y electric field components of the incident beam. After the first reflection is generated on area 1, where only the x component is modulated, the beam is then imaged onto area 2 through a reflective type 4f (f3 = 75 cm) system in which QWP1 is inserted to spatially rotate the polarization state by 90°. After reflection from area 2, where, again, only the x component is modulated, the beam is then imaged onto QWP2 by using a second telescope consisting of L4 (f4 = 20 cm) and L5 (f5 = 30 cm). QWP2 may be rotated to transform two linearly polarized OAM eigenstates into another pair of orthogonally polarized OAM eigenstates and attain the VVBs. Finally, the generated beams are passed through Stokes polarimetry consisting of QWP3 and polarizer P2, the transmission axis of which is fixed on the x-axis. QWP3 is electrically controlled by a computer, and the resolution is set to be 3°. A CCD camera (Newport LBP-4-USB) is used to record the variation of intensity distributions as QWP3 is rotates by 360°. Hence, the point-to-point Stokes parameters on the beams cross section can be obtained. Afterwards, Stokes polarimetry is removed and the CCD camera is replaced by a Shack-Hartmann wavefront sensor (Throlabs, WFS150-5C camera mounted with AR coated lens arrays at a pitch 300 μm and effective focal length of 14 mm) to measure the OAM charge of VVBs.

Figure 2: Experimental setup of the double modulation scheme.
figure 2

L: lens, P: polarizer, HWP: half-wave late, QWP: quarter-wave plate, M: mirror. The inset at right-top corner shows an example of displaying two helical phase holograms with different topological charges of (m1, m2) = (8, −4) onto the SLM.

Full size image

Theoretical modeling of vectorial vortex beam generation

To begin with, we briefly review the fundamental principle of the double modulation scheme17. Because of the phase-only modulation effect of reflective SLM, the LC molecules are aligned in a parallel fashion in the x-direction relative to the laboratory reference frame. As a result, only the x component of the reflected modulated beam carries the designed phase information, while the y component does not. To encode the y component, the polarization state must be rotated by 90° so that the x and y components are inverted. This explains why the modulation scheme uses both a SLM that is divided into two equal areas to modulate the incident beam twice and a reflective-type 4f system combined with a QWP to rotate the polarization state, as shown in Fig. 2. It should be mentioned that the extinction ratio of our calibrated SLM is about −18 dB (shown in the supplementary information) and, therefore, the y component will also be phase modulated in each modulation process. This may cause small errors in our experimental results.

As demonstrated in the supplementary information, the Jones vector of the resultant modulated-beam after passing through the double modulation system is given by

where and are two orthogonally polarized OAM eigenstates with topological charges of m1 and m2, respectively. Δφ denotes the relative phase offset between the eigenstates; thus, it is related to the choice of origin of the azimuthal φ-coordinate. As described in Fig. 2, θ is the angle between the polarization of the initial linearly polarized beam and the x-axis, and it controls the weights of the two orthogonal eigenstates. A comparison of equations (1) and (12) reveals that c1 = cos θ and c2 = sin θ, respectively; therefore, a theoretical OAM charge can be obtained by substituting c1 and c2 into equation (10). The polarization patterns of the VVBs generated based on equation (12) are measured experimentally by Stokes polarimetry. The point-to-point Stokes parameters over the transverse plane can be retrieved from several intensity patterns recorded using a CCD camera (details are given in the methods section). For measuring the OAM charge, Stokes polarimetry is replaced with a Shack–Hartmann sensor. The sensor consists of an array of lenses of the same focal length such that each microlens generates a spot on the sensor. The spot shift between the actual spot position and its corresponding reference position is proportional to the local skew angle of the Poynting vectors with respect to a beam axis20,24,25. Thus, this non-interferometric technique enables us to infer an actual OAM charge of VVBs.

Generation results and discussion

As mentioned previously, the QWP2 in Fig. 2 is employed to control the polarizations of two orthogonal OAM eigenstates, and the HWP controls their weighting factors. The experimental results of three different polarization eigenstates are presented in the following subsections.

Circular polarization eigenstates

In this subsection, the slow axis of QWP2 in Fig. 2 is set to 45° such that and in equation (12) are the right-handed circular polarization (RCP) and left-handed circular polarization (LCP) states, respectively. Figure 3 shows the corresponding experimental results obtained using different parameters. Here, black and blue marks in the first, second, and third columns represent the ideally linear and right-handed polarization states, respectively. The first row of the figure shows a generally polarized CVB. The second and third rows show the results obtained using higher indexes of m1 and m2. A comparison of simulated and experimentally measured SOP reveals that they are in good qualitative agreement for all results. At the same time, we also show the measured results of orientation and ellipticity angles of polarization ellipses in the second and third columns. The fourth column shows the intensity patterns of light behind a polarizer. The patterns obtained exhibit three extinction regions on the beam cross section. Our simulations indicate that, as a general rule, the total number of angularly distributed extinction regions around the beam axis is |m1 − m2|. Moreover, when the value of θ deviates from 45°, the contrast of the intensity pattern in the fourth column reduces because of the impurity of the linear polarization states. The last column shows the intensity patterns of light without passing through a polarizer; all of the intensity patterns obtained display a donut-shaped distribution.

Figure 3: VVBs constructed by circularly polarized OAM eigenstates.
figure 3

The first column shows simulated SOP, where the black and blue marks represent linear and right-handed polarization states, respectively. The second and third columns show measured SOP with angles of orientation and ellipticity of polarization ellipses. The fourth column shows the transmitted intensity patterns of light behind a polarizer with its transmission axis in the x direction. The last column shows intensity patterns of light without passing through a polarizer. Associated parameters in each row are (a) (m1, m2) = (−1, 1), θ = 45°, and Δφ = 90°, (b) (m1, m2) = (3, 6), θ = 45°, and Δφ = 0°, (c) (m1, m2) = (3, 6), θ = 30°, and Δφ = 0°.

Full size image

Linear polarization eigenstates

In this subsection, the slow axis of QWP2 in Fig. 2 is set to 0° such that and are the y- and x- linearly polarized eigenstates, respectively. To understand how SOP is affected by Δφ, Fig. 4(a,b) show the experimental results obtained using (m1, m2) = (1, 2), θ = 45°, and different Δφ values. Figure 4(c,d) show the experimental results obtained with higher indexes of (m1, m2). In addition, we consider the effect of swapping the indexes of (m1, m2) on SOP. A comparison of Fig. 4(a,b) reveals that a change in Δφ influences the spatial rotation of SOP with respect to a beam axis. We carried out a series of simulations (results not shown) and found that the polarization distribution on the beam rotates through an angle Δφ/(|m1 − |m2|) about a beam axis for a given shifted value of Δφ; this distribution shows counterclockwise and clockwise rotations, respectively, for positive and negative values of Δφ. A comparison of Fig. 4(c,d) reveals that swapping the indexes of (m1, m2) leads to inversion of the handedness of SOP, but the intensity patterns remain the same regardless of the presence of a polarizer. A comparison of the simulated and experimentally obtained SOP reveals that they are in good qualitative agreement. The fourth and fifth columns show the intensity patterns of light behind a polarizer with its transmission axis at 45° and 0°, respectively. As can be seen, when the polarizer axis is set to 45°, which is orthogonal to some local linear polarization states on the beam, the contrast of the intensity patterns is high. However, as indicated in the fifth column, this contrast disappears when the polarizer is oriented to 0° because the polarizer is no longer orthogonal to any local polarization state. The last column shows the intensity patterns of light that has not passed through a polarizer. As in the case of circular eigenstates, all obtained patterns feature a donut-shaped intensity distribution.

Figure 4: VVBs constructed by linearly polarized OAM eigenstates.
figure 4

The first column shows simulated SOP, where the blue and red ellipses, respectively, represent the right- and left-handed polarization states. The second and third columns show measured SOP with angles of orientation and ellipticity of polarization ellipses. The fourth and fifth columns show transmitted intensity patterns of light behind a polarizer with its transmission axis in the 45° and 0° directions, respectively. The last column shows intensity patterns of light without passing through a polarizer. Associated parameters in each row are (a) (m1, m2) = (1, 2), θ = 45°, and Δφ = −90°, (b) (m1, m2) = (1, 2), θ = 45°, and Δφ = 0°, (c) (m1, m2) = (3, 6), θ = 45°, and Δφ = 0°, (d) (m1, m2) = (6, 3), θ = 45°, and Δφ = 0°.

Full size image

Elliptical polarization eigenstates

In this subsection, the slow axis of QWP2 in Fig. 2 is set to 22.5°, and the corresponding eigenstates are sketched in the supplementary Fig. S5 online. The effect of introducing Δφ is similar (results not shown) to those of the linear eigenstates. The experimental results of different indexes of (m1, m2) where θ = 45° and Δφ = 0° are shown in Fig. 5. There is a good agreement between the simulated and experimentally measured SOP in the figure. The fourth and fifth columns show the intensity patterns of light behind a polarizer with its transmission axis respectively set to 45° and 0° with respect to the x-axis. The intensity patterns depend on the orientation of a polarizer, as in the case of linear eigenstates. The last column shows the intensity patterns of light that has not passed through a polarizer. Similar to previous results, there is a donut-shaped intensity distribution when a polarizer is not used.

Figure 5: VVBs constructed by elliptically polarized OAM eigenstates.
figure 5

The first column shows the simulated SOP, where the blue and red ellipses are the right- and left- handed polarization states, respectively. The second and third columns show measured SOP with angles of orientation and ellipticity of polarization ellipses. The fourth and fifth columns show transmitted intensity patterns of light behind a polarizer with its transmission axis in the 45° and 0° directions, respectively. The last column shows intensity patterns of light without passing through a polarizer. Associated parameters in each row are (a) (m1, m2) = (1, 2), θ = 45°, and Δφ = 0°, (b) (m1, m2) = (3, 6), θ = 45°, and Δφ = 0°.

Full size image

Thus far, we have considered only the SOP of VVBs. Another important characteristic of light is the OAM charge. As pointed out in equation (11), the Pancharatnam phase can be divided into two independent parts, and each of which is discussed in the following subsections.

• Case with θ = 45°.

In the case of θ = 45°, equally weighted eigenstates leading the Pancharatnam phase and OAM charge are as follows

The experimental results of different sets of (m1, m2) are shown in Fig. 6. Figure 6(a,b) correspond to the same differences but different sums of (m1, m2); in particular, the sum of m1 and m2 in Fig. 6(b) is zero. Figure 6(c,d) correspond to another pair of values of sums and differences. The first two columns of Fig. 6 show the measured SOP, as well as the orientation and ellipticity angles of the polarization ellipses. Those figures with the same values of (m1 − m2) reveal the same SOP, as indicated by equation (1). In practice, referring to Fig. 2, the distance from QWP3, in which the VVBs are generated, through Stokes polarimetry to the CCD camera is about 8 cm; hence, SOP evolution during propagation cannot be ignored13. This condition is confirmed by the measured phase difference δ (x, y) on the transverse plane shown in the third column, which is obtained by substituting the measured Stokes parameters into supplementary equations (S4) and (S5). The structure of δ (x, y) around the beam center is distorted for  ≠ 0, but it remains stable otherwise. The fourth column shows the displacement of focal spots between the actual spot position and its corresponding reference position, as measured by the Shack–Hartmann sensor. A substantial amount of curl around the beam axis for  ≠ 0 may be observed; the opposite is true when is zero. The length and direction of each arrow correspond to the projection of the local Poynting vector onto the wavefront sensor plane, which is perpendicular to the beam axis20. Hence, for higher values of , the azimuthal component of the local Poynting vector is larger, yielding longer displacement of the spot shifts pointing toward the azimuthal direction. A comparison of Fig. 6(a,c) reveals that the opposite sign of yields the reverse spatial evolution of the Poynting vector. The last column shows the intensity patterns obtained by using a conventional CCD camera instead of Stokes polarimetry. These patterns show that the size of the central dark spot increases with increasing sum of the modulus of m1 and m2, as will be discussed in the next subsection. The screw angle (γ ≡  = ), which is the angle between the φ- and z- components of the Poynting vectors20, can be obtained by projecting the transverse displacement of the focused spots onto the φ direction with respect to the beam axis, and subsequently dividing it by the focal length of the lens arrays of the wavefront sensor. A comparison between the theoretical and the measured screw angles at different beam radii is shown in Fig. 7, where the dashed lines (square points) are theoretical (measured) values of γ, and each color corresponds to each row of Fig. 6. As can be seen, there is good agreement between the theoretical and the measured results at all positions other than those close to the central singularity of a beam. The average OAM charge obtained by averaging the measurements for radii of 0.2 mm to 2 mm together with the corresponding standard deviation (SD) are listed on the side of Fig. 7. It can be found that the value of SD is proportional to due to the larger central dark spot at the beam center yielding to inaccurate measurement.

Figure 6: SOP and Poynting vector distributions of VVBs at elliptical eigenstates for θ = 45°.
figure 6

The first two columns show the measured SOP, as well as the orientation and ellipticity angles of polarization ellipses. The blue and red ellipses are the right- and left-handed polarization states, respectively. The third column shows the distribution of δ (x, y). The fourth column shows the displacements of focal spots on the Shack–Hartmann sensor plane. The last column shows the intensity patterns of light without passing through a polarizer. Associated parameters in each row are (a) (m1, m2) = (−3, −7),  = −5, (b) (m1, m2) = (2, −2),  = 0, (c) (m1, m2) = (4, 6),  = 5, (d) (m1, m2) = (2, 4),  = 3. All of the above parameters correspond to the same values of θ = 45° and Δφ = 0°.

Full size image
Figure 7: Measured skew angle γ of Poynting vectors at different beam radii.
figure 7

Each curve corresponds to each row of Fig. 6. The average OAM charge and standard deviation are listed on the side.

Full size image

• Case with m1 = −m2.

In the case of m1 = −m2, the Pancharatnam phase and OAM charge are

Both of them now depend on the weighted coefficients as well as the values of (m1, m2). The experimental results of different sets of (m1, m2) are shown in Fig 8. Figure 8(a,b) correspond to completely different values of (m1 − m2). Figure 8(b,c) correspond to equal but opposite signs of (m1 − m2). By contrast, the value of θ in Fig. 8(d) is specifically set to 45°, and the theoretical value of is zero. The first two columns of Fig. 8 show the measured SOP. The second column shows the distribution of δ (x, y) on the transverse plane. No distortion of δ (x, y) around the beam center is observed, regardless of the value of ; by contrast, as seen in the third column of Fig. 6, only when is zero δ (x, y) is not distorted. Actually, this distortion is due to the different Gouy phases of the two OAM eigenstates26,27. The fourth column of Fig. 8 shows the displacement of focal spots as measured by the Shack–Hartmann sensor. As expected, higher values of result in larger amounts of curl around a beam axis. The opposite sign of also leads to the reverse spatial evolution of the Poynting vectors. The last column presents the intensity patterns of light without passing through a polarizer. Similar to the previous fifth columns of Fig. 6, the size of the central dark spot increases as the sum of the modulus of m1 and m2 increases, likely because of the diffraction behavior of each OAM eigenstate. Based on the diffraction theory28, the larger the topological charge of the OAM mode, the larger is the local spatial frequency and the more likely it is that rays with larger skew angles with respect to the z-axis will be produced during propagation. Thus, larger values of |m1 + m2| yield larger radii of the central dark spot. This inference can be verified by comparing the fourth columns of Figs 6(b) and 8(d). These two cases correspond to the zero value of and show no obvious azimuthal component of the Poynting vectors. However, the energy spread of light in the radial direction is significant in the latter case because of the larger value of |m1 + m2|. Figure 9shows the measured screw angles of Poynting vectors at different beam radii, where different colors correspond to the respective rows of Fig. 8. As can be seen, there is good agreement between the theoretical (dashed lines) and the measured results (square points). The fluctuation for each curve is larger when the measurements are close to the central point, where the intensity is too low yielding to inaccurate measurement. Finally, it should be mentioned that while only VVBs constructed by two orthogonally polarized elliptical OAM eigenstates are described in this work, similar results can also be obtained for another pair of orthogonal polarization states.

Figure 8: SOP and Poynting vector distributions of VVBs at elliptical eigenstates for m1 = −m2.
figure 8

The first two columns show the measured SOP, as well as the orientation and ellipticity angles of polarization ellipses. The blue and red ellipses are the right- and left-handed polarization states, respectively. The third column shows the distribution of δ (x, y). The fourth column shows the displacements of focal spots on the Shack–Hartmann sensor plane. The last column shows the intensity patterns of light without passing through a polarizer. Associated parameters in each row are (a) (m1, m2) = (6, −6), θ = 30°, and  = 3, (b) (m1, m2) = (10, −10), θ = 30°, and  = 5, (c) (m1, m2) = (−10, 10), θ = 30°, and  = −5, (d) (m1, m2) = (10, −10), θ = 45°, and  = 0. All of the above parameters correspond to the same value of Δφ = 0°.

Full size image
Figure 9: Measured skew angle γ of Poynting vectors at different beam radii.
figure 9

Each curve corresponds to each row of Fig. 8. The average OAM charge and standard deviation are listed on the side.

Full size image

Conclusion

In this paper, we successfully generated a variety of VVBs with different polarization patterns and OAM charges based on the double reflection of a single SLM. The polarization patterns of the generated fields were analyzed by using Stokes polarimetry, while OAM charge was measured using a Shack–Hartmann wavefront sensor. We confirmed that the SOP around the beam axis becomes unstable during wave propagation if the Gouy phases of the two OAM eigenstates are unequal. Both the experimentally measured SOP and OAM charge of the generated VVBs are close to the theoretical values. In addition, we demonstrated that both polarization patterns and OAM charges can be controlled individually by using the proposed system.

Methods

Measurement of the Stokes parameters

The passage of light through an optical element may change its polarization state. Using Stokes parameters, the action of optical elements on the Stokes parameters can be completely described in the Stokes space. In this representation, a polarization state is represented by a Stokes vector, as expressed in equation (17), and the matrix of the optical element is represented by the Mueller matrix. Therefore, the Stokes vector of the outgoing beam can be obtained by carrying out matrix multiplication, as given in equation (18).

where Si (i = 0, …, 3) in equation (17) are the Stokes parameters of the incident light. As shown in Fig. 2, VBBs to be analyzed is sent through a rotating QWP3 and then through a polarizer P2 whose transmission axis is fixed along the x-axis. Subsequently, a CCD camera is used to record the beam intensity as a function of the rotation angle of QWP3. Thus, the Stokes vector of the outgoing beam passing through Stokes polarimetry can be obtained by

where and in equation (19) can be written as,

where and represent the Stokes vectors of the incident and outgoing beams, respectively, is the Muller matrix of the polarizer P2, is the Mueller matrix of the QWP3, the phase retardation Γ of which is π/2, and the slow axis of which makes an angle θ with the x-axis. The intensity pattern of I(θ) recorded on the camera is closely related to the first element of . After some algebra, the intensity variation versus rotation angle of θ presents the following form

Therefore, the Stokes parameters of VVBs can be obtained by using Fourier series analysis of the intensity pattern I(θ). We emphasize here that, because VVBs possess different SOP on the transverse plane, point-to-point Fourier series analysis must be performed over the entire x–y plane. When the Stokes parameters are obtained, other polarization parameters, such as the orientation and ellipticity angles of polarization ellipses, ψ and χ, can also be obtained by

Additional Information

How to cite this article: Yang, C.-H. et al. Independent Manipulation of Topological Charges and Polarization Patterns of Optical Vortices. Sci. Rep. 6, 31546; doi: 10.1038/srep31546 (2016).