Abstract
Recently, the layered semimetal WTe2 has attracted renewed interest owing to the observation of a non-saturating and giant positive magnetoresistance (~105%), which can be useful for magnetic memory and spintronic devices. However, the underlying mechanisms of the giant magnetoresistance are still under hot debate. Herein, we grew the stoichiometric and non-stoichiometric WTe2 crystals to test the robustness of giant magnetoresistance. The stoichiometric WTe2 crystals have magnetoresistance as large as 3100% at 2 K and 9-Tesla magnetic field. However, only 71% and 13% magnetoresistance in the most non-stoichiometry (WTe1.80) and the highest Mo isovalent substitution samples (W0.7Mo0.3Te2) are observed, respectively. Analysis of the magnetic-field dependent magnetoresistance of non-stoichiometric WTe2 crystals substantiates that both the large electron-hole concentration asymmetry and decreased carrier mobility, induced by non-stoichiometry, synergistically lead to the decreased magnetoresistance. This work sheds more light on the origin of giant magnetoresistance observed in WTe2.
Similar content being viewed by others
Introduction
Magnetoresistance (MR) is the change of electrical resistance under the application of a magnetic field. The materials with large MR can generate great potential applications in magnetic sensors1, magnetic information storage2 and so on. Recently, giant (~1.5 × 105% at 2 K and 9 Tesla magnetic field) and non-saturated MR is observed in two-dimensional (2D) layered transition-metal dichalcogenides WTe23. It leads to a series of works to study the novel physical properties of WTe2, such as superconductivity with Tc as high as 7 K under external mechanical pressure4 and possible quantum spin Hall effect in monolayer WTe2 with bulk electronic energy band-gap as large as 100.0 meV5. Certainly, the origin of extremely large MR is not only an important physical problem, but also valuable to device application of WTe2. As it was proposed, the main physical origin of giant MR is attributed to the nearly perfect compensation of electron and hole pockets3. This opinion is supported by subsequent Fermi surface determination by angle-resolved photoemission spectroscopy (ARPES)6, as well as suppressed MR under external mechanical pressure7.
However, recent work based on detailed ARPES claims that there are more subtle details in electronic band structure and abstract Fermi surface morphology in WTe28. Quantum oscillation of MR (Shubnikov-de-Haas oscillation) substantiates that there are multiple fermion pockets9. Some studies find evidences for spin-orbit split bands in WTe2. Spin-orbit split bands suppress the inter- and intra-band backscattering10. In addition, a latest study implies that the large MR in WTe2 also may be related to the crystal quality or carrier mobility11 and the more apparent decreased effect of MR to aliovalent doping (Re and Ta) over simple isovalent substitution (Mo-doping) and the different growth method also support it12. The physical origin of extremely large MR observed in WTe2 therefore is still an open question.
In this work, considering the above-mentioned confusion, we intentionally introduce the non-stoichiometry and isovalent doping Mo in WTe2 to investigate the dependence among electron-hole asymmetry, carrier mobility and MR. Our systematic MR and Hall effect measurements substantiate the extremely large MR in stoichiometric WTe2. But large MR is disappeared in non-stoichiometric and isovalent Mo substitution WTe2 crystals. Based on analysis of magnetic-field dependent MR, both enlarged electron-hole concentration asymmetry and decreased mobility synergistically lead to the decreased MR in doped WTe2. From the viewpoint of real application, our result suggests that significant MR is strongly dependent on the stoichiometry of WTe2.
Results
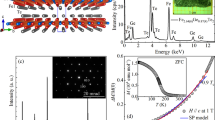
The optical micrograph of the synthesized crystals is shown in Fig. 1(a). The crystals show metallic luster and sheet-shape morphology. And the largest sample can be reached to 9 × 5 × 0.5 mm3. The XRD patterns of single crystal W1−xMoxTe2−y samples are depicted in Fig. 1(b). Only the (00l) reflections are observed in these curves. It suggests that the exposed surface of crystals (see Fig. 1(a)) belongs to ab-plane and the thinnest dimension is along the c-axis. To show the effect of Mo substituted and non-stoichiometric on the lattice constant clearly, we plot the c-axis lattice parameter dc for all W1−xMoxTe2−y samples in Fig. 1(c). It displays that the c-axis lattice parameter dc decreases monotonically with increasing y or x. As a result, we suggest that the Mo4+ ions enter into W-sites, due to the ionic radius of Mo4+ ions (0.65 Å) being smaller than that of W4+ (0.66 Å), which gives rise to the decrease in the lattice parameter dc13. By the same mechanism, the lack of Te element also can lead to the decrease of the lattice parameters (see the black line of Fig. 1(c)). Figure 1(d) plots the EDS spectra of three representative samples of WTe2, WTe1.80 and W0.7Mo0.3Te2 crystals. These results prove that the samples with varied chemical composition are obtained.
(a) The representative optical micrograph of the as-grown W1−xMoxTe2−y single crystals. (b) The XRD patterns of the single crystal W1−xMoxTe2−y samples. (c) The c-axis lattice parameter dc as a function of Mo-substituting level x and non-stoichiometric level y, respectively. (d) The EDS spectra of three representative samples (WTe2, WTe1.80 and W0.7Mo0.3Te2).
Figure 2(a) depicts the typical temperature-dependent ab-plane resistivity ρxx, measured from 2 K to 300 K, for the stoichiometric and non-stoichiometric WTe2 crystals. They all show the metallic behavior but with different residual resistance. Quantitatively, the residual resistance of WTe2, WTe1.90, WTe1.85 and WTe1.80 are 8.0 × 10−6, 5.4 × 10−5, 5.9 × 10−5 and 7.4 × 10−5 Ω·cm, respectively. One can see that stoichiometric WTe2 sample has the minimum residual resistance. It infers that non-stoichiometry does induce the high density of defects/impurities, which in turn increases the residual resistance in non-stoichiometric WTe2 crystals14. The temperature-dependent resistances of stoichiometric and Mo substituted WTe2 crystals are presented in Fig. 2(b). As the same as the non-stoichiometric WTe2−y, they also demonstrate the metallic behavior and raising the Mo-substituting concentration increases the residual resistance of W1−xMoxTe2 samples too. The relationship between the residual resistance ρres, as well as the residual resistivity ratio (RRR) and Mo-substituting concentration x and non-stoichiometric concentration y are presented in Fig. 2(c). It substantiates that upon raising the Te deficiency and the Mo concentration, the density of defects/impurities in non-stoichiometric WTe2 samples gradually increases.
(a) The temperature-dependent ab-plane resistivity ρxx (from 2 K to 300 K) of the stoichiometric and non-stoichiometric WTe2 crystal samples. (b) The temperature-dependent resistivity ab-plane ρxx (from 2 K to 300 K) of the stoichiometric and Mo substituted WTe2 crystals. (c) The residual resistance ρres (red line) and the RRR value (green line) as a function of Mo-substituting level x and non-stoichiometric level y, respectively.
In order to study the influence of the chemical composition changes on the MR property of WTe2, the transport properties of stoichiometric WTe2 crystals were investigated firstly. Figure 3(a) shows the curves of MR vs external magnetic field for WTe2 crystals under variable temperatures. The MR is defined as
(a) The relationship between magnetoresistance (MR) and magnetic field of stoichiometric WTe2 single crystals under several temperatures, with magnetic field applied along the c-axis and scanned from 0 to 9 T. (b) Fast Fourier Transform (FFT) spectra at 2 K. The six major frequencies are observed. (c) The relationship between Hall resistivity (ρxy) along ab-plane of stoichiometric WTe2 crystal and magnetic-field measured at variable temperatures. (d) ρxy–B curve measured at 2 K and the corresponding fitting by two-band model.

where ρxx and B are longitudinal resistance and magnetic field, respectively. One can see that curves of the MR are parabola-like up to 9 T. And the most impressive feature is that the MR of stoichiometric WTe2 reaches around 3100% at 2 K and 9 T. Though this value is smaller than that in the first paper reporting the giant MR (~105%) in WTe23, it is quite comparable to results in other reports4,15,16. As can be seen in Fig. 3(a), distinct Shubnikov-de-Haas oscillations are observed in MR-magnetic field curve measured at 2 K, which is related to the quantum behavior of the electrons or holes. And it is inferred that there is high enough carrier mobility in this crystal to observe the quantum oscillation17. After subtracting the smooth background of the MR measured at 2 K, the fast Fourier transform (FFT) analysis was carried out on the Shubnikov-de-Haas oscillations18. As shown in Fig. 3(b), we have identified four peaks: F1 ≈ 86.4 T, F2 ≈ 129.6 T, F3 ≈ 146.2 T and F4 ≈ 159.6 T, which are consistent with the previous results9. In accordance with previous analysis, the oscillations of F1 and F4 come from hole, while the left two oscillations do electrons9. The observed peaks of 247.9 T and 274.6 T can be attributed to sum frequencies F1 + F4 and F2 + F3, respectively. Accordingly, by assuming isotropic parabolic dispersion, the electron and hole’s concentrations can be extracted as 3.2 × 1019 cm−3 and 3.7 × 1019 cm−3, respectively. To quantify the degree of the mismatch of electron and hole concentrations, we define the electron-hole concentration asymmetry factor k as

where ne and nh represent the electron and hole concentration, respectively. The small dimensionless value of asymmetry factor k represents the small mismatch between the electron and hole concentrations. The value of k in as-grown stoichiometric WTe2 can be calculated as 0.0725.
To further support above discussion, magnetic-field dependent Hall resistivity (ρxy) is presented in Fig. 3(c) at variable temperatures. The negative and linear magnetic-field-dependent ρxy at high temperature (above 50 K) reveals that the dominant carrier is electron. According to the formula RH = B/ne (where RH, n and e represent the Hall resistivity14, carrier concentration and electron charge, respectively), the electron carrier concentration of WTe2 at 300 K is 3.0 × 1020 cm−3. But with the temperature decreasing, the dependence of ρxy on magnetic field obviously deviates from the linear relationship (below around 50 K). This suggests that hole and electron carriers contribute together for the electrical transport in WTe2 crystal. This is consistent to the result of the Shubnikov-de-Haas oscillation. So a classical two-band model was used to fit the non-linear relationship between Hall resistivity and magnetic field at 2 K (Fig. 3(d)). In two-band model, the Hall resistivity is described as14:

where μe and μh are the carrier mobility of electron and hole, respectively. Here, with the best fitting shown in Fig. 3(d), the values of electron and hole mobility are 4.0 × 103 cm2V−1s−1 and 5.2 × 103 cm2V−1s−1, respectively. In the fitting, the electron and hole concentrations extracted from Shubnikov-de-Haas oscillation are used. It should be noted that below around 50 K, the Hall curves deviate from the linear relationship gradually. Simultaneously, the MR is increased gradually up to 3100% at 2 K. It strongly suggests that extremely large MR is coincident to high carrier mobility and comparable concentration of electron and hole at low temperatures.
The non-stoichiometric and Mo substituted WTe2 samples provide a platform to adjust the Fermi level and enhanced impurity scattering. It in turn affects the mismatch degrees of the electron and hole concentrations, as well as carrier mobility14. Compared with the stoichiometric WTe2 single crystals, the MR of non-stoichiometric WTe2−y (y = 0.10, 0.15, 0.20) and Mo substituted WTe2 W1−xMoxTe2 (x = 0.05, 0.10, 0.15, 0.30) single crystals is smaller (Fig. 4). Quantitatively, the MR of WTe2−y (y = 0.10, 0.15, 0.20) and W1−xMoxTe2 (x = 0.05, 0.10, 0.15, 0.30) measured at 2 K and 9 T magnetic field are 640%, 86%, 71%, 210%, 33%, 31% and 13%, respectively.
Here we analyze the physical origin of MR evolution in stoichiometric and non-stoichiometric WTe2 crystals. According to the two-band model with electrons and holes, the MR can be written as14:

The meanings of symbols are the same as those described above. For simplifying this complex equation, we assume that electron and hole have same carrier mobility, so μe = μh = μ (μ is the mean mobility). This approximation is often used to describe the MR in the semimetals19. Thus, Eq. (4) can be simplified as

So we firstly used this formula to fit all the curves at various temperatures and get the value of asymmetry factor k and the mean mobility μ for stoichiometric WTe2 (shown in Fig. 3(a)), summarized in Fig. 5(a). One can see that the mobility μ remains fairly steady below 10 K but gradually decreases with increasing the temperature above 20 K. On the contrary, the asymmetry factor k has a reverse trend. With the decrease of μ and the enlarging of k, the MR of stoichiometric WTe2 gradually decreases. Thus we speculate the large MR effect in WTe2 material may be related to both electron-hole concentration asymmetry and the carrier mobility. In order to verify the assumption, we further used the equation (5) to fit all the curves at 2 K and get the value of asymmetry factor k and the mean mobility μ for each composition W1−xMoxTe2−y (shown in Fig. 4). As depicted in Fig. 5(b), upon raising the lack of Te element or increasing Mo-substituting concentration, the electron-hole concentration asymmetry enlarges and carrier mobility decreases. Both these two factors lead to the decreased MR in non-stoichiometric and Mo substituted WTe2. Figure 5(c) shows the asymmetry factor k and the mean mobility μ dependent MR colored picture, which is calculated from the equation (5). As shown in Fig. 5(c), one can find that the highest MR is observed at the bottom-right region with the equal electron-hole concentration and the largest mobility. In the real material systems, the colored discrete points of each composition distributes along the dash line in Fig. 5(c). Thus, one can conclude that electron-hole concentration asymmetry, induced by both non-stoichiometric and Mo-substituting, leads to the dramatically depressed MR in WTe2 system. Furthermore, the new lesson we learned here is that decreased carrier mobility also can lead to the depressed MR. Quantitatively, there is only 13% MR in W0.7Mo0.3Te2. In this case, the corresponding electron-hole concentration asymmetry (k) and mobility (μ) are 0.68, 5.7 × 102 cm2V−1s−1, respectively. Compared with stoichiometric WTe2 crystal, μ of W0.7Mo0.3Te2 is much smaller than stoichiometric one. Thus it suggests that both electron-hole concentration and carrier mobility play the crucial role on the MR in WTe2 material.
(a) Temperature dependence of MR (i), squared mobility μ2 (μ ≈ μe ≈ μh, the unit of μ is m2V−1s−1) (ii) and squared electron-hole concentration asymmetry factor k2  (iii) for stoichiometric WTe2 crystal (shown in Fig. 4(a)). (b) The MR (i), μ2 (ii) and k2 (iii) for each composition W1−xMoxTe2−y (shown in Fig. 4). (c) The dependence of MR on k2 and μ2 at 2 K calculated by
(iii) for stoichiometric WTe2 crystal (shown in Fig. 4(a)). (b) The MR (i), μ2 (ii) and k2 (iii) for each composition W1−xMoxTe2−y (shown in Fig. 4). (c) The dependence of MR on k2 and μ2 at 2 K calculated by  . Colored spots are experimental data extracted from Fig. 5(b).
. Colored spots are experimental data extracted from Fig. 5(b).
Here we’d like to compare aforementioned work to current available similar works. Flynn, et al. also found that the significant MR in 1% Mo, Re or Ta doped WTe2 is nearly lost, which is attributed to the large electron-hole asymmetry induced by Re or Ta-doping12. But it can be seen that the specimens in this work are ceramic ones. We suspect that the low carrier mobility in ceramic samples also contributes the decreased MR therein. Ali, et al. compared the MR of WTe2 synthesized by both chemical vapor transport and self-flux methods11. It claimed that WTe2 synthesized by self-flux method has larger mobility than one by chemical vapor transport, which leads to larger MR in WTe2 synthesized by flux method. Compared these works to current one, it is obvious that based on our systematic single crystals W1−xMoxTe2−y samples, the relationship among MR, electron-hole asymmetry and carrier mobility is clearly revealed.
Conclusions
In summary, we intentionally synthesized the non-stoichiometric and Mo substituted WTe2 single crystals to study the effect of electron-hole concentration asymmetry on the MR of WTe2. It is substantiated that no matter in non-stoichiometric or in Mo substituted WTe2 single crystals, there is dramatically decreased magnetoresistance. The quantitative magnetoresistance fitting substantiates that non-stoichiometric and Mo-substituting not only induces the electron-hole concentration asymmetry, but also generates the decreased mobility. These two factors synergistically lead to the dramatically decreased magnetoresistance in non-stoichiometric WTe2 crystals. Thus, it is crucial to obtain high purity single samples to realize the equal amount of electrons and holes, as well as high carrier mobility. Our work will provide an important clue for the exploring of such large MR materials.
Methods
Single crystals of W1−xMoxTe2−y were grown by a chemical vapor transport method using Br2 as the transport agent. All polycrystalline samples of W1−xMoxTe2−y were synthesized from high purity elemental powders W (99.99%), Mo (99.99%) and Te (99.999%) by solid state reaction in evacuated quartz tubes. It is worthwhile to mention that in nominal stoichiometric WTe2 sample described below, the mole ratio of W and Te in raw materials is set as 1:2. Afterwards, mixtures of as-prepared polycrystalline W1−xMoxTe2−y and Br2 (about 5 mg/L) were loaded into the sealed evacuated quartz tube and then placed at a double zone furnace with a temperature gradient between hot end 850 °C and cold end 750 °C to grow crystals for 10 days. Then all the crystals samples were characterized by X-ray diffraction (XRD) measurement in an X-ray diffractometer (Ultima III Rigaku) using Cu-Kα radiation with 2θ scanned from 10° to 70°. The detailed elemental compositions of the as-grown crystals were determined by a scanning electron microscope (SEM, FEI-Quanta) equipped with an energy-dispersive spectroscopy (EDS) spectrometer. Standard six-probe method was used for the electrical resistivity, MR and Hall resistance measurements. These characterizations were performed in a 9 T physical properties measurement system (PPMS, Quantum Design). The magnetic field was perpendicular to the ab-plane in our magneto-transport measurements.
Additional Information
How to cite this article: Lv, Y.-Y. et al. Dramatically decreased magnetoresistance in non-stoichiometric WTe2 crystals. Sci. Rep. 6, 26903; doi: 10.1038/srep26903 (2016).
References
Daughton, J. et al. Magnetic Field Sensors Using GMR Multilayer. IEEE Trans. Magn. 30, 4608–4610 (1994).
Prinz, G. A. Magnetoelectronics. Science 282, 1660–1663 (1998).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2 . Nature 514, 205–208 (2014).
Pan, X. C. et al. Pressure-driven dome-shaped superconductivity and electronic structural evolution in tungsten ditelluride. Nat. Commun. 6, 7805 (2015).
Qian, X. F., Liu, J. W., Fu, L. & Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344–1347 (2014).
Pletikosić, I., Ali, M. N., Fedorov, A. V., Cava, R. J. & Valla, T. Electronic Structure Basis for the Extraordinary Magnetoresistance in WTe2 . Phys. Rev. Lett. 113, 216601 (2014).
Cai, P. L. et al. Drastic Pressure Effect on the Extremely Large Magnetoresistance in WTe2: Quantum Oscillation Study. Phys. Rev. Lett. 115, 057202 (2015).
Jiang, J. et al. Signature of Strong Spin-Orbital Coupling in the Large Non-saturating Magnetoresistance Material WTe2 . Phys. Rev. Lett. 115, 166601 (2015).
Zhu, Z. W. et al. Quantum Oscillations, Thermoelectric Coefficients and the Fermi Surface of Semimetallic WTe2 . Phys. Rev. Lett. 114, 176601 (2015).
Rhodes, D. et al. Role of spin-orbit coupling and evolution of the electronic structure of WTe2 under an external magnetic field. Phys. Rev. B. 92, 125152 (2015).
Ali, M. N. et al. Correlation of crystal quality and extreme magnetoresistance of WTe2 . EPL, 110, 67002 (2015).
Flynn, S., Ali, M. & Cava, R. J. The Effect of Dopants on the Magnetoresistance of WTe2. arXiv:1506.07069 (2015).
Shannon, R. D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. A32, 751–767 (1976).
Ziman, J. M. Electrons and phonons-the theory of transport phenomena in solids pp. 490–495 (Oxford University Press, 1960).
Kong, W. D. et al. Raman scattering investigation of large positive magnetoresistance material WTe2 . Appl. Phys. Lett. 106, 081906 (2015).
Xiang, F. X., Veldhorst, M., Dou, S. X. & Wang, X. L. Multiple Fermi pockets revealed by Shubnikov-de Haas oscillations in WTe2 . EPL, 112, 37009 (2015).
Xiang, F. X., Wang, X. L., Veldhorst, M., Dou, S. X. & Fuhrer, M. S. Observation of topological transition of Fermi surface from a spindle torus to a torus in bulk Rashba spin-split BiTeCl. Phys. Rev. B. 92, 035123 (2015).
Singleton, J. Band theory and electronic properties of solids pp. 91–97 (Oxford University Press, 2001).
Zhang, L. Y. et al. Tunable semimetallic state in compressive-strained SrIrO3 films revealed by transport behavior. Phys. Rev. B. 91, 035110 (2015).
Acknowledgements
We’d like to acknowledge the financial support from the National Natural Science Foundation of China (51032003, 51472112, 11374149 and 10974083), the Major State Basic Research Development Program of China (973 Program) (2015CB921203) and the Program for New Century Excellent Talents in University (NCET-09-0451). Y.-Y. Lv acknowledges the financial support from the Graduate Innovation Fund of Nanjing University (2015CL11). We acknowledge very helpful discussions with Hongtao Yuan.
Author information
Authors and Affiliations
Contributions
S.-H.Y. and Y.-Y.L. performed the crystal growth in assist of D.-J.L., Y.-Y.L. and F.Z. determined the structure content and the elemental composition of the crystals. B.-B.Z. and Y.-Y.L. conducted the transport measurements. Y.-B.C., B.-B.Z. and Y.-Y.L. analyzed the data and refined the measurements. J.Z., Y.-F.C. and Y.L.C. contributed to the result analysis. Y.-B.C., B.-B.Z. and Y.-Y.L. co-wrote the manuscript. S.-H.Y., S.-T.Z., M.H.L. and Z.K.L. revised the manuscript. B.P. and X.L. did some additional experiments in reviewing manuscripts. All authors discussed the results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Lv, YY., Zhang, BB., Li, X. et al. Dramatically decreased magnetoresistance in non-stoichiometric WTe2 crystals. Sci Rep 6, 26903 (2016). https://doi.org/10.1038/srep26903
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep26903
This article is cited by
-
Strong modulation of carrier effective mass in WTe2 via coherent lattice manipulation
npj 2D Materials and Applications (2022)
-
Composition and temperature-dependent phase transition in miscible Mo1−xWxTe2 single crystals
Scientific Reports (2017)
-
Investigation on the phase-transition-induced hysteresis in the thermal transport along the c-axis of MoTe2
npj Quantum Materials (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.