Non-commutativity measure of quantum discord

Abstract

Quantum discord is a manifestation of quantum correlations due to non-commutativity rather than entanglement. Two measures of quantum discord by the amount of non-commutativity via the trace norm and the Hilbert-Schmidt norm respectively are proposed in this paper. These two measures can be calculated easily for any state with arbitrary dimension. It is shown by several examples that these measures can reflect the amount of the original quantum discord.

Introduction

The characterization of quantum correlations in composite quantum states is of great importance in quantum information theory^1,2,3,4,5,6. It has been shown that there are quantum correlations that may arise without entanglement, such as quantum discord (QD)⁴, measurement-induced nonlocality (MIN)⁶, quantum deficit⁷, quantum correlation induced by unbiased bases^8,9 and quantum correlation derived from the distance between the reduced states¹⁰, etc. Among them, quantum discord has aroused great interest in the past decade^{11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30}. It is more robust against the effects of decoherence¹³ and can be a resource in quantum computation^31,32, quantum key distribution³³ remote state preparation^34,35 and quantum cryptography³⁶.

Quantum discord is initially introduced by Ollivier and Zurek⁴ and by Henderson and Vedral⁵. The idea is to measure the discrepancy between two natural yet different quantum analogs of the classical mutual information. For a state ρ of a bipartite system A + B described by Hilbert space H_a ⊗ H_b, the quantum discord of ρ (up to part B) is defined by

where, the minimum is taken over all local von Neumann measurements Π^b, is interpreted as the quantum mutual information, is the von Neumann entropy, , and with , k = 1, 2, …, dim H_b. Calculation of quantum discord given by Eq. (1) in general is NP-complete since it requires an optimization procedure over the set of all measurements on subsystem B³⁷. Analytical expressions are known only for certain classes of states^{15,16,20,38,39,40,41,42,43,44,45}. Consequently, different versions (or measures) of quantum discord have been proposed^{19,24,25,46,47}: the discord-like quantities in⁴⁶, the geometric measure⁴⁷, the Bures distance measure²⁴ and the trace norm geometric measure¹⁹, etc. Unfortunately, all of theses measures are difficult to compute since they also need the minimization or maximization scenario.

Let {|i_a〉} be an orthonormal basis of H_a. Then any state ρ acting on H_a ⊗ H_b can be represented by

where E_ij = |i_a〉〈j_a| and . That is, assume that Alice and Bob share a state ρ, if Alice take an ‘operation’

on her part, then Bob obtains the local operator B_ij (Note here that, the ‘operation’ Θ_ij is not the usual quantum operation which admits the Kraus sum respresentation). Quantum discord is from non-commutativity: D(ρ) = 0 if and only if B_ijs are mutually commuting normal operators^47,48. It follows that the non-commutativity of the local operators B_ijs implies ρ contains quantum discord. The central aim of this article is to show that, for any given state written as in Eq. (2), its quantum discord can be measured by the amount of non-commutativity of the local operators, B_ijs. In the following, we propose our approach: the non-commutativity measures. We present two measures: the trace norm measure and the Hilbert-Schmidt norm one. Both of them can be calculated for any state directly via the Lie product of the local operators. We then analyze our quantities for the Werner state, the isotropic state and the Bell-diagonal state in which the original quantum discord have been calculated. By comparing our quantities with the original one, we find that our quantities can quantify quantum discord roughly for these states.

Results

The amount of non-commutativity

Let X and Y be arbitrarily given operators on some Hilbert space. Then [X, Y] = XY − YX = 0 if and only if ||[X, Y]|| = 0, ||·|| is any norm defined on the operator space. That is, ||[X, Y]|| ≠ 0 implies the non-commutativity of X and Y. In general, ||[X, Y]|| reflects the amount of the non-commutativity of X and Y. Furthermore, for a set of operators Γ = {A_i : 1 ≤ i ≤ n}, the total non-commutativity of Γ can be defined by

In ref. 49, N(Γ) is used for measure the ‘quantumness’ of a quantum ensemble Γ when ||·|| is the trace norm ||·||_Tr, i.e., . We remark here that any norm can be used for quantifying the amount. It is a natural way that, for any state as in Eq. (2), the amount of its non-commutativity can be considered as the total non-commutativity of {B_ij}, N({B_ij}).

Non-commutativity measure of quantum discord

Let be a state acting on H_a ⊗ H_b as in Eq. (2). We define a measure of QD for ρ by

Similarly, we can define

where ||·||₂ denotes the Hilbert-Schmidt norm, i.e., . That is, if Alice takes Θ_ijs on her part, 1 ≤ i, j ≤ dim H_a, then Bob can calculate the amount of non-commutativity through the reduced operators B_ijs. By definition, it is obvious that i) D_N(ρ) ≥ 0, , both D_N and vanish only for the zero quantum discord states, i.e., iff D(ρ) = 0; ii) both D_N and are invariant under the local unitary operations as that of the quantum discord, i.e., and for any unitary operator U_a/b acting on H_a/b (this implies that D_N and are independent on the choice of the local orthonormal bases: if with respect to the local orthonormal basis {|i_a〉 |j_b〉} and with respect to another local orthonormal basis , then and for some local unitary operators U_a and U_b); iii) for any ρ. By the definitions, it is clear that both D_N and can be easily calculated for any state.

Let |ψ〉 be a pure state with Schmidt decomposition . Then

where Ω = {(k, l): either i < k ≤ j ≤ l or k = i and l = j if i < j; i ≤ k < l if i = j}, Ω′ = {(k, l): i < k ≤ j ≤ l if i < j; i ≤ k < l if i = j}. Therefore, D_N(|ψ〉〈ψ|) = 0 (or ) if and only if |ψ〉 is separable. For the maximally entangled state in a d ⊗ d system, it is straightforward that whenever d = 2, whenever d = 3 and 4 whenever d = 4, whenever d = 2, whenever d = 3 and whenever d = 4. D_N and reach the maximum values only on the maximally entangled one.

It is worth mentioning here that both D_N and are defined without measurement, so the way we used is far different from the original quantum discord and other quantum correlations (note that all the measures of the quantum correlations proposed now are defined by some distance between the state and the post state after some measurement). In addition, it is clear that D_N(ρ) and are continuous functions of ρ since both the trace norm and Hilbert-Schmidt norm are continuous. In²⁸, a set of criteria for measures of correlations are introduced: (1) necessary conditions ((1-a)–(1-e)), (2) reasonable properties ((2-a)–(2-c)) and (3) debatable criteria ((3-a)–(3-d)). One can easily check that our quantity meets all the necessary conditions as a measure of quantum correlation proposed in²⁸ (note that the condition (1-d) in²⁸ is invalid for D_N(ρ) and ). The continuity of D_N and meets the reasonable property (2-a) (note: (2-b) and (2-c) are invalid since these two conditions are associated with measurement-induced correlation). (7) and (8) guarantee the debatable property (3-a). (3-c) and (3-d) are not satisfied as that of the original quantum discord while (3-b) is invalid for D_N and . That is, all the associated conditions that satisfied by the original quantum discord are met by our quantities. From this perspective, D_N and are well-defined measures as that of the original quantum discord.

Comparing with the original quantum discord

In what follows, we compare the non-commutativity measures D_N and with quantum discord D for several classes of well-known states and plot the level surfaces for the Bell-diagonal states. These examples will show that D_N and reflect the amount of quantum discord roughly: D_N and increase (resp. decrease) if and only if D increase (resp. decrease) for almost all these states (see Figs 1, 2, 3). D_N ≥ D and for almost all these states while there do exist states such that D_N < D and (see Fig. 3(a,b)). In addition, D_N and characterize quantum discord in a more large scale than that of D roughly. For the two-qubit pure state , we can also calculate that whenever λ₁ > a with a ≈ 0.3841 while whenever λ₁ < a and whenever λ₁ > b with b ≈ 0.4279 while whenever λ₁ < b.

Figure 1

The measures D, D_N and as a function of α for the Werner state when (a-1) d = 2, (b-1) d = 3 and (c-1) d = 4 and that of the isotropic state when (a-2) d = 2, (b-2) d = 3 and (c-2) d = 4. For both the Werner state and the isotropic state, D_N and are monotonic functions of D.

Figure 2

The surfaces of constant D_N and as a function of c₁, c₂ and c₃ for: (a) D_N = 0.05, (b) D_N = 0.1 and (c) D_N = 0.3; (a′) , (b′) and (c′) .

Figure 3

The measures D, D_N and as a function of p for (a) ρ₁, (b) ρ₂, (c) ρ₃ and (d) ρ₄.

Werner states

The Werner states of a d ⊗ d dimensional system admit the form⁵⁰,

where and are projectors onto the symmetric and antisymmetric subspace of respectively, is the swap operator. Then

and

The three measures of quantum correlation, i.e., D_N, and D, are illustrated in (a-1), (b-1) and (c-1) in Fig. 1 for comparison, which reveals that the curves for D_N and have the same tendencies as that of D.

Isotropic states

For the d ⊗ d isotropic state

where is the maximally entangled pure state in . Then

and

The three measures of quantum correlation, i.e., D_N, and D, are illustrated in (a-2), (b-2) and (c-2) in Fig. 1 for comparison. We see from this figure that the curves for D_N and have the same tendencies as that of D. It also implies that i) for both the Werner states and the isotropic states, D_N and are close to each other, ii) D is close to D_N and with increasing of the dimension d for the Werner states, which in contrast to that of the isotropic states.

Bell-diagonal states

The Bell-diagonal states for two-qubits can be written as

where the σ_js are Pauli operators, {|β_ab〉} are four Bell states . Then

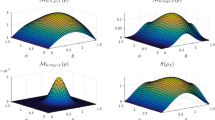
In Fig. 2, the level surfaces of D_N and are plotted respectively. By comparing them with that of D in ref. 51, we find that the trends of D_N and are roughly the same as that of D: D_N and increase when D increases roughly and vice versa. (The geometry of the set of the Bell-diagonal states is a tetrahedron with the four Bell states sit at the four vertices, the extreme points of tetrahedron (i.e., (−1, 1, 1), (1, −1, 1), (1, 1, −1) and (−1, −1, −1)), see Fig. 1 in ref. 51 for detail.)

Especially, we consider

and

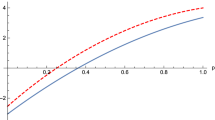
The three measures of quantum correlation, i.e., D_N, and D, are compared in Fig. 3. For ρ₁, ρ₃ and ρ₄, the variation trends of D_N and coincide with that of D while for ρ₂ the curves of D_N and have the same tendency as that of D roughly. In addition, one can see that i) D_N and can both lager than and smaller than D, namely, there is no order relation between D and the two previous measures, ii) while the behavior of both measures D_N and is quite similar, they are quite different from that of D.

Going further, we can quantify the symmetric quantum discord, i.e., the quantum discord up to both part A and part B. Let {|k_b〉} be an orthonormal basis of H_b, then any ρ acting on H_a ⊗ H_b admits the form

with F_kl = |k_b〉〈l_b|. Here, A_kl = Tr_b(1_a ⊗ |l_b〉〈k_b|ρ) are local operators on H_a. Let

where ||·|| is the trace norm, or the Hilbert-Schmidt norm, or other norms. Then i) and if and only if it is a classical-classical state (ρ is called a classical-classical state if with p_ij ≥ 0 and ); ii) is invariant under the local unitary operations. We can conclude that quantifies the amount of the symmetric quantum discord of ρ.

Discussion

New measures of quantum discord has been proposed by means of the amount of the non-commutativity quantified by the trace norm and the Hilbert-Schmidt norm. Our method provides two calculable measures of quantum discord from a new perspective: unlike the original quantum discord and other quantum correlations were induced by some measurement, the two non-commutativity quantities we presented were not defined via measurements. Both of them can be calculated directly for any state, avoiding the previous optimization procedure in calculation. The nullities of our measures coincide with that of the original quantum discord and they are invariant under local unitary operation as well. The examples we analyzed indicate that, when comparing our quantities with the original quantum discord, although they are different and even have large difference for some special states, the non-commutativity measures reflect the original quantity roughly overall. We can conclude, to a certain extent, that our approach can reflect the original quantum discord for the set of states with arbitrary dimension. On the other hand, the non-commutativity measures reflect quantum discord in a larger scale than that of the original quantum discord, we thus can use these measures to find quantum states with limited quantum discord or the maximal discordant states (especially for the states represented by one or two parameters), etc.

As usual, only the trace norm and the Hilbert-Schmidt norm are considered. In fact we can also use the general operator norm or other norms in the definitions of D_N and . In addition, Fig. 2 shows that the level surfaces of are nearly symmetric up to the four Bell states directions, which is very close to that of the quantum discord D (the level surfaces of D are symmetric up to the four Bell states directions⁵¹). Also note that the Hilbert-Schmidt norm is more easily calculated than the trace norm one, we thus use the Hilbert-Schmidt norm measure in general.