Abstract
We performed an unbiased structure search for low-lying energetic minima of neutral and charged palladium PdnQ (n = 2–20, Q = 0, + 1 and –1) clusters using CALYPSO method in combination with density functional theory (DFT) calculations. The main candidates for the lowest energy neutral, cationic and anionic clusters are identified and several new candidate structures for the cationic and anionic ground states are obtained. It is found that the ground state structures of small palladium clusters are more sensitive to the charge states. For the medium size Pdn0/+/– (n = 16–20) clusters, a fcc-like growth behavior is found. The structural transition from bilayer-like structures to cage-like structures is likely to occur at n = 14 for the neutral and cationic clusters. In contrast, for the anionic counterparts, the structural transition occurs at Pd13–. The photoelectron spectra (PES) of palladium clusters are simulated based on the time-dependent density functional theory (TD-DFT) method and compared with the experimental data. The good agreement between the experimental PES and simulated spectra provides us unequivocal structural information to fully solve the global minimum structures, allowing for new molecular insights into the chemical interactions in the Pd cages.
Similar content being viewed by others
Introduction
There is active interest in the synthesis and electrochemical applications of palladium-based nanomaterials1. Of particular commercial potential is the replacement of platinum-based electrocatalysts with palladium-based ones. Overall, palladium clusters have attracted considerable attention in recent years. Fields of particular interest are hydrogen storage2, catalysis3,4, sensors5 and biomedicine6. Clusters are considered a new and challenging kind of molecular architecture, enabling the transition from few-atom assemblies, to nanoparticles and the bulk. Molecular science is facing unique problems, especially in the determination of stable structures and therefore explanations of the variation of the physicochemical properties. Several experiments7,8,9 confirm that small palladium clusters exhibit a novel ferromagnetism, although there is no magnetic moment both in the atomic state and in the bulk, due to the closed shell electronic (4d105s0) configuration of the atom. Recent breakthrough work10,11,12 clearly suggests that synthesized subnanometer palladium clusters can be stabilized. In practice, they exhibit enhanced catalytic properties in synthesis and in situ characterization methods of ultra-small metal clusters. Understandably, the stability of the molecular architectures and their electronic configuration is seen as a very important in the study of the ground state of palladium clusters.
The growth behavior and respective patterns of palladium clusters have been systematically studied. Kumar et al.13 presented an icosahedral growth pattern for neutral palladium clusters (n = 2–23, 55 and 147). Futschek et al.14 investigated the structure of small Pdn (n = 2–13) clusters and suggested that the favorable structures of Pd11, Pd12 and Pd13 clusters are the fcc fragments of bulk palladium. Zhang et al.15 examined closely four types of possible structural motifs (fcc like, decahedron based, icosahedron based and prolate ellipsoid-based) and advanced the view that medium-sized Pdn (n = 15–25) clusters prefer fcc-like structures. The case of the Pd13 cluster merits particular attention. Reddy et al.16 suggested the ground state of this cluster favors a compact packing. A lower energy buckled biplanar structure was predicted by Chang and Chu17. An even lower energy structure than the above was found in a distorted hexagonal bilayer-like structure by Piotrowski et al.18. Subsequently, through an integrated theoretical and experimental analysis, a bilayer ground-state structure was determined by Köster et al.19 Two more studies are particularly interesting. Nava et al.20 presented a reference study on neutral, large Pdn (n = 2–309) clusters; and the average bond length in Pdn (n = 4–309) clusters was investigated by Krüger et al.21
Most of the theoretical studies focus on neutral palladium clusters. Few studies are available for the cationic and anionic species22,23,24. We deem essential a systematic investigation of neutral and charged medium-sized palladium clusters Pdn0/+/– (n = 2–20). The present study on medium-sized clusters is not restricted to molecular geometries and stabilities but also investigates electric and magnetic properties. In addition, we have calculated for the first time the relevant photoelectron spectra. As these are directly comparable to experimental data, this comparison constitutes a valuable test of the reliability of our computational strategy.
The central aim of our work is the systematic, in-depth study of the structural evolution and properties of palladium (neutral, cationic and anionic) clusters by combining the unbiased CALYPSO method with density functional theory techniques. Thus, we are able to advance a fundamental understanding of the ground state geometric configurations of neutral, cationic and anionic Pdn0/+/– (n = 2–20) clusters. Subsequently, we reexamine carefully the structure of specific neutral, cationic and anionic low-energy isomers of palladium clusters that have been the target of previous investigations by other workers. Finally, we explore closely the physical mechanism of the growth behavior of palladium clusters and provide new insights that should be of importance to further theoretical and experimental studies. The paper is organized as follows: we present and discuss the findings pertaining to geometrical structures, photoelectron spectra, relative stabilities, magnetic properties and polarizabilities of the ground state structures in the following. Then, our conclusions are summarized. Finally, details of the computational method are concisely described.
Results and Discussion
Geometric structures
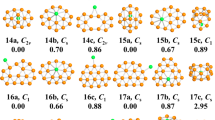
The global minimum structures for the lowest energy neutral and charged palladium clusters in the size range of n = 2–20 are displayed in Fig. 1. Previously reported isomers, from experiment and theory, are successfully reproduced with our structure search method. Representative metastable isomers of neutral and charged clusters, together with their point group symmetries and relative energies are displayed in Figs S1–S3 in the Supporting Information (SI). The corresponding electronic state, point group symmetry, binding energy (Eb) and HOMO−LUMO gap (Egap) of the ground state structures are also determined and listed in Table S1 (see SI).
Previous findings22,24 on small (n ≤ 7) clusters revealed that the neutral and corresponding charged palladium clusters have similar geometric configurations and follow the same structural evolution. The respective ground state structures found in our searches are in accord with those previously reported experimental and theoretical findings, which corroborates the reliability of our theoretical method. We then carefully investigate small PdnQ clusters to pinpoint the characteristic transformations brought by the addition or removal of an electron. In the case of n = 2–4, 6 and 7, neutral palladium clusters often have the same or quite similar structures to the corresponding charged palladium clusters. A striking structural transformation occurs at n = 5. Neutral and anionic Pd50/– clusters have similar trigonal bipyramid structures, while the cationic Pd5+ cluster is a pyramid with a bent base. It is worth mentioning that the new structure of cationic Pd5+ is 0.06 eV lower in energy than the trigonal bipyramid structure reported by Kalita et al.22.
Although such small PdnQ clusters have been extensively studied, relatively few studies are available for medium or large size PdnQ. As is well known, the true ground state structures for neutral palladium clusters in the range of n = 8–20 have been the object of some controversy. The marked disagreement between early studies confirms the existing difficulty in reliably identifying the structural characteristics of medium and large PdnQ clusters. Turning our attention to the range of n = 8–20, we observe a fcc-like growth pathway for neutral Pdn (n = 16–20) clusters, in agreement with the related findings of Zhang et al.15 and Mu et al.25 For charged clusters, we note a significant structural transformation. This structural evolution of medium-sized charged Pdn+/– (n = 16–20) clusters has, to our knowledge, not been noticed before. Neutral and charged clusters display three entirely different structures for n = 10, 11 and 14. For n = 10 and 11, the charged clusters favor corresponding distorted neutral structures. It is clear that the neutral Pd14 cluster favors a bilayer-like structure with two face centered hexagonal surfaces. This configuration lies 0.13 eV lower than the cage-like structure with three capped atoms of the metastable cluster in Fig. S1 (see SI). The cationic Pd14+ cluster is most stable in a face-centered bilayer-like configuration that has not been reported previously. In the case of the anionic Pd14– cluster, the ground state structure is found to be the cage-like structure that is the metastable Pd14 structure. The anionic Pd14– cluster is thus the first cage-like structure amongst Pd clusters as the size of the clusters increases. More generally, all neutral and charged clusters can be viewed as cage-like structures for n ≥ 15. It is safe to conclude that for medium-sized palladium clusters there exists a structural transition point from bilayer-like structures to cage-like structures. The transition occurs at n = 14 for the neutral and cationic clusters and at n = 13 for the anionic cluster.
As discussed above, we find that small palladium clusters are more sensitive to the charge state than the larger clusters. Several new lowest-energy structures are identified and shown here for cationic and anionic clusters. These promising candidates have never been reported as ground state structures. To the best of our knowledge, there are few findings about medium-sized cationic and anionic palladium clusters to compare with ours or to be considered for a reexamination. Hence, our results for these clusters should provide a valuable basis for further investigations.
Photoelectron spectra
To verify the accuracy of the ground state structures of palladium clusters we have calculated the adiabatic detachment energies (ADEs = Eoptimized neutral – Eoptimized anion) and the vertical detachment energies (VDEs = Eneutral at optimized anion geometry – Eoptimized anion). The computed results are summarized in Table 1, along with available theoretical and experimental values. As shown in Table 1, the calculated ADE and VDE values are in good agreement with the experimental values26,27 for all cases with the notable exception of n = 3. There, the discrepancy between our theoretical and experimental values is almost 0.50 eV, but our calculations agree well (deviate by only 0.14 eV) with other theoretical results24. For the larger size clusters (n = 16–20), unfortunately, no experimental data are available to compare with our results.
A deeper understanding of the cluster’ electronic properties is obtained through the simulation of the photoelectron spectra (PES) of anionic palladium clusters (n = 2–20) as obtained using TD-DFT. The theoretical along with the experimental PES spectra26,27 are shown in Fig. 2. In this work, the full width at half maximum of Gaussian function of anionic Pdn– (n = 2–20) clusters is in the range of 0.05–0.40 eV. Restricted by experimental conditions, the overall experimental PES is mainly used to estimate the position of the first strong maximum peak. From an experimental viewpoint, the binding energy of first major peak represents the vertical detachment energy (VDE). In particular, the experimental PES for anionic Pdn– (n = 7–13) clusters show only one prominent peak in the region 1.0–3.0 eV. To make the comparison with experimental PES, we align the VDE of simulated spectra with the experimental spectra. From Fig. 2, the VDE values of simulated PES are found to be in quite good agreement with the experimental data for anionic clusters (n = 2–13), while there is a discrepancy for n = 3. This may be due to that palladium has a variety of isotopes (102Pd, 104Pd, 105Pd, 106Pd, 108Pd and 110Pd), which increase the difficulty of precise measurement for experimental PES. The theoretical PES for the anionic clusters (n = 16–20) show several recognizable peaks in the range of binding energy 3.0–4.0 eV. In general, the PES data should also provide a definitive electronic fingerprint for the ground state structures. We hope that the theoretical PES values together with the calculated ADE and VDE of Pdn– (n = 16–20) clusters will provide valuable information for future experimental investigations.
The calculated photoelectron spectra of Pdn– (n = 2–20) clusters, together with the available experimental data for comparison.
The first major peaks are marked with vertical arrows. The experimental PES of Pdn– (n = 3–8) clusters come from ref. 26, while the rest of experimental PES come from ref. 27.
Relative stability
The inherent stability of the palladium clusters studied in this work is determined by computing the binding energy per atom (Eb), defined as

E is the total energy of the clusters. The average binding energy (Eb) of a cluster is a measure of its thermodynamic stability. For Pdn0/+/– clusters, the calculated results of Eb as a function of cluster size n are displayed in Fig. 3(a). As evidenced from Fig. 3(a), the Eb values of neutral Pdn cluster are always much lower than their charged counterparts. In addition, the Eb values of neutral and charged clusters increase monotonically with cluster size, except for a dip found for cationic and anionic clusters at n = 7. As expected, the difference between the binding energy of clusters and bulk gets smaller with increasing cluster size and the average binding energy approaches the cohesive energy of 3.89 eV/atom of bulk palladium28.
Another important parameter to measure the relative stabilities of the most stable clusters is the size-dependent second energy difference (∆2E), which can be calculated by

The calculated results of ∆2E as a function of cluster size are shown in Fig. 3(b). It is well-known that a maximum of ∆2E relative to its immediate neighbors indicates an enhanced stability of a particular cluster. Therefore, the values of ∆2E can be considered as an alternative measure of the stability of clusters, where the most stable clusters are identified from the maxima of ∆2E. Figure 3(b) reveals conspicuous odd-even oscillations for each state. For neutral clusters, the odd size clusters show a greater stability compared to their even counterparts for Pdn (7 < n < 15) clusters. Moreover, several pronounced peaks are found at n = 4, 6, 9, 11, 13 and 16, implying strong relative stability. A similar oscillatory trend is found for anionic Pdn– clusters in the size range of n > 8, while cationic Pdn+ (2 ≤ n ≤ 8) clusters present an opposite oscillating behavior. In addition, some local maxima of ∆2E are observed at n = 4, 6, 8, 11, 14 and 17 for cationic clusters as well as n = 3, 6, 9, 11, 13, 15 and 17 for anionic clusters.
The electronic energy gap (Egap) reflects the energy cost for an electron to jump from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). A large Egap usually correlates with remarkable kinetic stability. The calculated values of HOMO–LUMO energy gaps for the ground state of Pdn0/+/– (n = 2–20) clusters are listed in Table S1. We plot the Egap values as a function of cluster size n in Fig. 3(c). It is interesting to notice that the curves for neutral and charged clusters show a fluctuant downward trend, indicating that small clusters are more stable than the larger clusters. At the same time, we find some conspicuous peaks, Pd5, Pd7, Pd10, Pd13, Pd17 and Pd19 for neutral clusters, Pd4+, Pd8+, Pd11+, Pd15+ and Pd17+ for cationic clusters, as well as Pd3–, Pd6–, Pd9–, Pd11–, Pd13–, Pd17– and Pd19– for anionic clusters. These peaks reflect stronger local stability of the clusters compared to their neighbors.
Note that the Pd4+ cluster corresponds to a maximum of the ∆2E, the second energy difference, but also to a remarkable peak of Egap, the HOMO–LUMO gap. This suggests its stability among neutral and charged clusters. We have calculated the one-electron energy levels and the corresponding molecular orbitals for the Pd4+ cluster (see Fig. 4). Despite their different shapes, there are three kinds of orbitals: s-type molecular orbital, p-type molecular orbital and d-type atomic orbital. We also observe that d-type atomic orbital dominate the molecular orbitals diagram of the cluster. From Fig. 4, we infer that the HOMO and LUMO of Pd4+ occupy an s-type molecular orbital and d-type atomic orbital, respectively. Regarding the lower occupied levels, the HOMO-1 possesses s-type molecular orbital, while HOMO-2 to -6 resemble d-type atomic orbitals. The LUMO + 1 and LUMO + 2 levels resemble d-type atomic orbitals, while higher LUMO + q (q = 3–6) levels occupy p-type molecular orbitals. In addition to Td symmetry, the Pd4 + cluster displays characteristic degeneration which may give rise to the largest Egap (2.58 eV).
We performed a chemical bonding analysis based on the localized orbitals resulting from the AdNDP algorithm. The AdNDP approach is an ideal tool for deciphering the nature of bond localization and delocalization in clusters; in short it takes advantage of the electron pair as the unit of chemical bonding by partitioning the electron density matrix into nc−2e terms (n ranges from 1 to the maximum number of atomic centers). The AdNDP analysis of Pd4+ cluster is shown in Fig. 5. The AdNDP analysis indicates eight lone pairs (LPs) with an occupation number ON = 1.996 |e|, four other LPs with ON = 1.994 |e|, six 2c–2e Pd-Pd σ bonds with ON = 1.996 |e| and one 4c–2e σ bond with lower ON = 1.844 |e|. It is interesting to note that each atom has three lone pair localized bonds.
To further advance our understanding of the dynamical stability of the Pd4+ cluster, show its vibrational IR and Raman spectra in Fig. S4 (see SI). The insets show the eigenvectors of the Pd4+ cluster for the modes with the highest IR intensity or Raman activity. It is worth noting that both can be considered as spectroscopic fingerprints to confirm the existence of Pd4+ cluster between different species and different isomers in future experiments.
Fragmentation channels
It is known that fragmentation processes may involve dissociation barriers. However, from a purely energetic point of view, the fragmentation energies (Ef) of the most stable clusters can be expressed as

In this work, we have considered all possible fragmentation channels for neutral and charged clusters and the respective values for Ef are listed in Table S2–S4 (see SI). By definition, the preferred dissociation channels are those yielding the lowest Ef29. In the case of negative Ef for particular fragmentation channels, the initial clusters are unstable and could dissociate spontaneously by releasing a |Ef| amount of energy. In our calculations, the energy of all possible fragmentation channels is positive, indicating that the initial clusters are stable and must absorb energy to induce the fragmentations. The Pdn0/+/– → Pdn-10/+/– + Pd channels are then the routes favored by all palladium clusters (n = 2–20). I.e., the neutral and charged palladium clusters tend to lose individual atoms when absorbing energy.
The Ef values for the respective most favorable fragmentation channels are plotted as a function of cluster size in Fig. 3(d). Highest stability, associated with an energy maximum, is evidenced for Pd4 for neutrals and Pd17– for anions as well as Pd4+ for cations. Moreover, several local maximums compared to their neighbors are observed: Pd6, Pd9, Pd11, Pd13, Pd16 and Pd18 for neutrals, Pd6+, Pd8+, Pd11+, Pd14+ and Pd17+ for cations and Pd6–, Pd11–, Pd13– and Pd15– for anions. It should be stressed again that the Pd4+ cluster is characterized by remarkable stability. This is in accordance with the above analysis based on the second energy difference ∆2E and the energy gap Egap. As a consequence, an analysis of the ∆2E, Egap and Ef values, provides the following magic numbers: (i) n = 13 for neutral clusters; (ii) n = 4, 8, 11 and 17 for cationic clusters; (iii) n = 6, 11, 13 and 17 for anionic clusters.
Magnetic properties
The total spin magnetic moments of Pdn0/+/– clusters as a function of cluster size n are shown in Fig. 6(a). In addition to several peaks and troughs, a typical step-like behavior of the total magnetic moment is observed in the lowest-energy state of the neutral clusters, a fact previously reported by other research groups13,25,28. A very similar situation is also observed for cationic and anionic clusters. We regard this striking variation as a consequence of the difference of their geometrical configurations, as the magnetic energy is extremely sensitive to minor geometry changes28. For the sake of comparison, the magnetic moment per atom (μB /atom) is calculated and compared to theoretical values by Kumar et al.13 in Table 1. It is worth mentioning that there is a consensus in the recent theoretical literature15,25 that the highly symmetric icosahedral structures tend to possess large magnetic moments as reported by Kumar et al.13 Although the results of neutral palladium clusters agree very well with those of Kumar et al.13 at n < 8, the various structures of Pdn (n = 8–15) clusters clearly favor lower magnetic moment values. Cox et al.7 reported that Pd13 has a magnetic moment of ~ 0.4 μB at 98 K. This is in excellent agreement with our theoretical value of 0.46 μB at absolute zero. From a purely theoretical point of view, below the Curie temperature an increase in temperature leads to a decrease of the magnetic moment. Our computed value is reasonable. As we mentioned earlier, the bulk magnetic moment of palladium is zero, leading us to expect a decrease of the magnetic moment with increasing cluster size.
In order to probe the origin of the magnetic step-like behavior of palladium clusters, we analyze the total density of states (TDOS) and the projected density of electronic states (PDOS). Because a large magnetic moment jump occurs at n = 14 for cationic clusters, the Pd13+ and Pd14+ clusters are examined and shown in Fig. 7. As evidenced by the diagram, extremely strong hybridization occurs between s, p and d states. By comparing the results of TDOS and PDOS of Pd13+ and Pd14+ clusters, it is observed that the total magnetic moments mainly come from d states below the Fermi level, while the s and p states produce nearly negligible contributions. However, an obvious hybridization between s, p and d states is observed for Pd13+ and Pd14+ clusters in the vicinity of the Fermi level. We also notice that the up-spin and down-spin sub-bands of the d states are substantially split when going from n = 13 to n = 14. This may result in an enhanced magnetic moment. This conclusion can is corroborated by the TDOS and PDOS of anionic Pd9– and Pd10– as well as neutral Pd15 and Pd16 clusters, as plotted in Fig. S4 (see SI).
Polarizabilities
The electric dipole moment and polarizability are closely related to the structural features and electronic properties of clusters. In terms of applications, the site-specific polarizabilities can be used to predict the optimal adsorption sites of an adsorbed molecule29. In this paper, we have calculated the mean polarizability per atom which is defined in terms of the components as  , where n is the number of atoms in the cluster. The calculated results and the electric dipole moments (μ) of the neutral and charged ground states are depicted in Fig. 6(b). The mean polarizability per atom and electric dipole moments of the neutral and charged clusters are also listed in Table S5 and S6 (see SI). On account of their high symmetries, the dipole moments of several clusters (Pd20/+/–, Pd4+/–, Pd6+/– and Pd7+/–) vanish. Notably, the addition or removal of an electron leads, as is the case of n = 4, 6 and 7, to significantly higher symmetry. This is the reason why the dipole moment of the charged clusters is zero. Furthermore, we note that our calculated polarizabilities for neutral and charged clusters are independent (see Fig. 6(b)). For the anionic clusters, the calculated
, where n is the number of atoms in the cluster. The calculated results and the electric dipole moments (μ) of the neutral and charged ground states are depicted in Fig. 6(b). The mean polarizability per atom and electric dipole moments of the neutral and charged clusters are also listed in Table S5 and S6 (see SI). On account of their high symmetries, the dipole moments of several clusters (Pd20/+/–, Pd4+/–, Pd6+/– and Pd7+/–) vanish. Notably, the addition or removal of an electron leads, as is the case of n = 4, 6 and 7, to significantly higher symmetry. This is the reason why the dipole moment of the charged clusters is zero. Furthermore, we note that our calculated polarizabilities for neutral and charged clusters are independent (see Fig. 6(b)). For the anionic clusters, the calculated  /n decrease monotonously with the cluster size n, with the notable exception of a peak occurring at n = 8. The presence of this peak is attributed to the lower symmetry of n = 8 compared to the high symmetry of Pdn– clusters in the range of n = 2–7. For the neutral clusters, owing to the different spin multiplicity, there is an apparent conflict compared to the singlet state value of Pd2 reported by Ma et al.30. As it is well established, relevant experiment findings31 and theoretical results22,32 point to a triplet for the ground state of diatomic palladium. So our result is more accurate. It is worth noting that earlier work by Li et al.33 reported mean dipole polarizability values of 58.3 (singlet) and 83.7 (triplet) e2a02Eh–1 for Pd2 (atomic units, 1 e2a02Eh–1 = 1.648778 × 10–41 C2m2J–1). Relying on a recommended theoretical value34 for the polarizability of the atom, α(Pd) = 32 e2a02Eh–1, we find that the differential-per-atom mean polarizability (DPA)35,36, defined for the Pdn cluster as
/n decrease monotonously with the cluster size n, with the notable exception of a peak occurring at n = 8. The presence of this peak is attributed to the lower symmetry of n = 8 compared to the high symmetry of Pdn– clusters in the range of n = 2–7. For the neutral clusters, owing to the different spin multiplicity, there is an apparent conflict compared to the singlet state value of Pd2 reported by Ma et al.30. As it is well established, relevant experiment findings31 and theoretical results22,32 point to a triplet for the ground state of diatomic palladium. So our result is more accurate. It is worth noting that earlier work by Li et al.33 reported mean dipole polarizability values of 58.3 (singlet) and 83.7 (triplet) e2a02Eh–1 for Pd2 (atomic units, 1 e2a02Eh–1 = 1.648778 × 10–41 C2m2J–1). Relying on a recommended theoretical value34 for the polarizability of the atom, α(Pd) = 32 e2a02Eh–1, we find that the differential-per-atom mean polarizability (DPA)35,36, defined for the Pdn cluster as

reaches a high value for the dimer: DPA(Pd2) ≈ 10 e2a02Eh–1. In the case of cationic clusters, we observe an upward fluctuant trend from n = 2 to n = 14 as well as an evident jump at n = 3. The value of  /n for cationic clusters is around 30.4 e2a02Eh–1 in the range of n = 15 to 20. In addition, we observe a clear convergence of the mean polarizability per atom
/n for cationic clusters is around 30.4 e2a02Eh–1 in the range of n = 15 to 20. In addition, we observe a clear convergence of the mean polarizability per atom  /n of neutral and charged clusters for relative large cluster sizes.
/n of neutral and charged clusters for relative large cluster sizes.
Conclusions
On the basis of the unbiased CALYPSO structure searching method and density functional theory calculations, we report a detailed investigation of neutral and charged palladium clusters. The most stable structures of the neutral clusters are compared with those of the charged clusters in the size range up to 20 atoms. The structure searches show that the ground state structures of small palladium clusters are more sensitive to the charge states than previously thought. A fcc-like growth behavior is found for the medium size Pdn0/+/– (n = 16–20) clusters. The photoelectron spectra of Pdn– clusters are simulated based on TD-DFT and compared with experimental data. The reasonable agreement between them indicates that our structure searches have very likely uncovered the actual ground state structures. The electronic and magnetic properties as well as fragmentation channels for the ground state Pdn (n = 2–20) clusters are also studied in detail for both neutral and charged Pd clusters. The lowest-energy tetrahedral structure of Pd4+ cluster with Td symmetry shows very high stability. The Pdn0/+/– → Pdn0/+/– + Pd channels are the favored fragmentation routes for all neutral, cationic and anionic clusters. Interestingly, a step-like magnetic behavior is observed for neutral and charged palladium clusters.
Methods
We performed an unbiased structure search for the lowest energy neutral, cationic and anionic palladium clusters in the size range of n = 2–20, respectively. We employed the CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) searching method37,38 coupled with DFT calculations for geometry optimization. This combined CALYPSO/DFT computational approach has been previously used to search for low-lying sulphur clusters39, boron clusters40 and boron doped silver clusters41. Within the CALYPSO structure search, we adopted the global version of the particle swarm optimization (PSO) algorithm to finely explore the potential energy surface for each cluster size. This method has been successfully used to predict correctly ground state structures for various systems42,43,44,45. In the CALYPSO structure search, the initial structures are randomly generated with the constraint of symmetries42. When a new structure is generated, the bond characterization matrix is calculated to check the similarity of this structure with others. After all the structures have been generated, the local structural optimizations are performed to eliminate the noise of energy surface and drive the systems to the local minima. We typically followed 30 generations to generate at least 1000 structurally different low-energy isomers for each size. Among the 1000–1200 isomers, the top fifty low-lying isomers are collected as candidates for the lowest-energy structure. Those structures with energy difference from the lowest-lying isomers less than 0.3 eV (usually about 20) are further optimized to identify the lowest-energy structure. The geometry optimizations are performed without symmetry constraints using the Gaussian 09 package46 and the B3LYP (Becke three-parameter-Lee–Yang–Parr)47,48 hybrid exchange-correlation functional. The pseudopotential relativistic LANL2DZ49 basis set for Pd is employed in all calculations. Harmonic vibrational frequencies are calculated at the same level of theory in order to ensure that the obtained optimized structures are true minima (no imaginary frequencies). The photoelectron spectrum of the anionic palladium clusters is simulated by calculating excited energies within the framework of time-dependent density functional theory (TD-DFT)50. The chemical bonding analysis presented here is obtained via the adaptive natural density partitioning (AdNDP) method51,52.
Additional Information
How to cite this article: Xing, X. et al. Insights into the geometries, electronic and magnetic properties of neutral and charged palladium clusters. Sci. Rep. 6, 19656; doi: 10.1038/srep19656 (2016).
References
Wu, P. et al. Multisource synergistic electrocatalytic oxidation effect of strongly coupled PdM (M=Sn, Pb)/N-doped graphene nanocomposite on small organic molecules. Sci. Rep-uk. 5, 14173–14182 (2015).
Langhammer, C., Zorić, I., Kasemo, B. & Clemens, B. M. Hydrogen storage in Pd nanodisks characterized with a novel nanoplasmonic sensing scheme. Nano Lett. 7, 3122–3127 (2007).
Fu, G.-T. et al. Polyhedral palladium-silver alloy nanocrystals as highly active and stable electrocatalysts for the formic acid oxidation reaction. Sci. Rep-uk. 5, 13703–13711 (2015).
Yu, Y. et al. Efficient visible-light photocatalytic degradation system assisted by conventional Pd catalysis. Sci. Rep-uk. 5, 9561–9566 (2015).
Yang, D. C., Carpena-Núñez, J., Fonseca, L. F., Biaggi-Labiosa, A. & Hunter, G. W. Shape-controlled synthesis of palladium and copper superlattice nanowires for high-stability hydrogen sensors. Sci. Rep-uk. 4, 3773–3778 (2014).
Kapdi, A. R. & Fairlamb, I. J. S. Anti-cancer palladium complexes: a focus on PdX2L2, palladacycles and related complexes. Chem. Soc. Rev. 43, 4751–4777 (2014).
Cox, A. J., Louderback, J. G., Apsel, S. E. & Bloomfield, L. A. Magnetism in 4d-transition metal clusters. Phys. Rev. B 49, 12295–12298 (1994).
Taniyama, T., Ohta, E. & Sato, T. Ferromagnetism of Pd fine particles. Physica B 237–238, 286–288 (1997).
Sampedro, B. et al. Ferromagnetism in fcc twinned 2.4 nm size Pd nanoparticles. Phys. Rev. Lett. 91, 237203 (2003).
Lee, S. et al. Oxidative decomposition of methanol on subnanometer palladium clusters: The effect of catalyst size and support composition. J. Phys. Chem. C 114, 10342–10348 (2010).
Judai, K., Abbet, S., Wörz, A. S., Heiz, U. & Henry, C. R. Low-temperature cluster catalysis. J. Am. Chem. Soc. 126, 2732–2737 (2004).
Stefan, V. et al. Subnanometre platinum clusters as highly active and selective catalysts for the oxidative dehydrogenation of propane. Nature Mater. 8, 213–216 (2009).
Kumar, V. & Kawazoe, Y. Icosahedral growth, magnetic behavior and adsorbate-induced metal-nonmetal transition in palladium clusters. Phys. Rev. B 66, 144413 (2002).
Futschek, T., Marsman, M. & Hafner, J. Structural and magnetic isomers of small Pd and Rh clusters: An ab initio density functional study. J. Phys.: Condens. Matter 17, 5927–5963 (2005).
Zhang, H., Tian, D. & Zhao, J. Structural evolution of medium-sized Pdn (n=15–25) clusters from density functional theory. J. Chem. Phys. 129, 114302 (2008).
Reddy, B. V., Khanna, S. N. & Dunlap, B. I. Giant magnetic moments in 4d clusters. Phys. Rev. Lett. 70, 3323–3326 (1993).
Chang, C. M. & Chou, M. Y. Alternative low-symmetry structure for 13-atom metal clusters. Phys. Rev. Lett. 93, 133401 (2004).
Piotrowski, M. J., Piquini, P. & Da Silva, J. L. F. Density functional theory investigation of 3d, 4d and 5d 13-atom metal clusters. Phys. Rev. B 81, 155446 (2010).
Köster, A. M. et al. On the ground state of Pd13 . J. Am. Chem. Soc. 133, 12192–12196 (2011).
Nava, P., Sierka, M. & Ahlrichs, R. Density functional study of palladium clusters. Phys. Chem. Chem. Phys. 5, 3372–3381 (2003).
Krüger, S., Vent, S., Nörtemann, F., Staufer, M. & Rösch, N. The average bond length in Pd clusters Pdn, n=4-309: A density-functional case study on the scaling of cluster properties. J. Chem. Phys. 115, 2082–2087 (2001).
Kalita, B. & Deka, R. C. Stability of small Pdn (n=1–7) clusters on the basis of structural and electronic properties: A density functional approach. J. Chem. Phys. 127, 244306 (2007).
Reveles, J. U., Köster, A. M., Calaminici, P. & Khanna, S. N. Structural changes of Pd13 upon charging and oxidation/reduction. J. Chem. Phys. 136, 114505 (2012).
Moseler, M., Häkkinen, H., Barnett, R. N. & Landman, U. Structure and magnetism of neutral and anionic palladium clusters. Phys. Rev. Lett. 86, 2545–2548 (2001).
Mu, Y. W. et al. Structures and magnetic properties of Pdn clusters (n=3–19) doped by Mn atoms. Phys. Rev. A 84, 053201 (2011).
Ganteför, G. & Eberhardt, W. Localization of 3d and 4d electrons in small clusters: The “Roots” of magnetism. Phys. Rev. Lett. 76, 4975–4978 (1996).
Ganteför, G., Gausa, M., Meiwes-Broer, K.-H. & Lutz, H. O. Photoelectron spectroscopy of silver and palladium cluster anions electron delocalization versus, localization. J. Chem. Soc. Faraday Trans. 86, 2483–2488 (1990).
Rogan, J. et al. The structure and properties of small Pd clusters. Nanotechnology 19, 205701–205709 (2008).
Akman, N., Tas, M., Özdoğan, C. & Boustani, I. Ionization energies, coulomb explosion, fragmentation, geometric and electronic structures of multicharged boron clusters Bn (n=2–13). Phys. Rev. B 84, 075463 (2011).
Ma, L., Wang, J. & Wang, G. Dipole polarizabilities of Pdn (n=2–25) clusters. Eur. Phys. J. D 67, 6–14 (2013).
Ho, J., Ervin, K. M., Polak, M. L., Gilles, M. K. & Lineberger, W. C. A study of the electronic structures of Pd2− and Pd2 by photoelectron spectroscopy. J. Chem. Phys. 95, 4845–4853 (1991).
Masafumi, H. & Hervé, D. Electronic structure of transition metal clusters from density functional theory. 1. transition metal dimers. J. Phys. Chem. 100, 565–572 (1996).
Li, C. S., Cao, Z. X., Wei, W., Lin, M. H. & Zhang, Q. E. DFT studies on the Pdn (n=2–13) clusters. Chem. J. Chin. Univ. 26, 116–120 (2005).
Schwerdtfeger, P. [Atomic static dipole polarizabilites] Atoms, molecules and clusters in electric fields-theoretical approaches to the calculation of electric polarizability [ Maroulis, G. (ed.)] [10–15] (World Scientific, Imperial College Press, 2006).
Maroulis, G., Begue, D. & Pouchan, C. Accurate dipole polarizabilities of small silicon clusters from ab initio and density functional theory calculations. J. Chem. Phys. 119, 794–797 (2003).
Maroulis, G. Dipole (hyper)polarizability and differential (hyper)polarizability in the antimony octamer Sb8 . J. Comput. Theor. Nanosci. 6, 886–893 (2009).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Jin, Y. Y. et al. Geometries, stabilities and fragmental channels of neutral & charged sulfur clusters: SnQ (n=3–20, Q=0, ±1). Phys. Chem. Chem. Phys. 17, 13590–13597 (2015).
Lv., J., Wang, Y. C., Zhu, L. & Ma, Y. M. B38: an all-boron fullerene analogue. Nanoscale 6, 11692–11696 (2014).
Jin, Y. Y. et al. Ab initio search for global minimum structures of pure and boron doped silver clusters. J. Phys. Chem. A 119, 6738–6745 (2015).
Lv, J., Wang, Y. C., Zhu, L. & Ma, Y. M. Particle-swarm structure prediction on clusters. J. Chem. Phys. 137, 084104 (2012).
Wang, Y. C. et al. An effective structure prediction method for layered materials based on 2D particle swarm optimization algorithm. J. Chem. Phys. 137, 224108 (2012).
Lu, S. H. et al. Self-assembled ultrathin nanotubes on diamond (100) surface. Nature Commun. 5, 3666–3672 (2014).
Zhu, L. et al. Reactions of xenon with iron and nickel are predicted in the earth’s inner core. Nature Chem. 6, 644–648 (2014).
Frisch, M. J. et al. Gaussian 09 (Revision C.0), Gaussian, Inc., Wallingford, CT, 2009).
Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Stephens, P. J., Devlin, F. J., Chabalowski, C. F. & Frisch, M. J. Ab-initio calculation of vibrational absorption and circular-dichroism spectra using density-functional force-fields. J. Phys. Chem. 98, 11623–11627 (1994).
Hay, P. J. & Wadt, W. R. Ab initio effective core potentials for molecular calculations. potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 82, 270–283 (1985).
Casida, M. E., Jamorski, C., Casida, K. C. & Salahub, D. R. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold. J. Chem. Phys. 108, 4439–4449 (1998).
Lu, T. & Chen, F. W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 33, 580–592 (2012).
Zubarev, D. Y. & Boldyrev, A. I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys. Chem. Chem. Phys. 10, 5207−5217 (2008).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos 11274235, 11304167 and 11574220), 973 Program of China (2014CB660804), Program for Science & Technology Innovation Talents in Universities of Henan Province (No. 15HASTIT020) and Open Project of State Key Laboratory of Superhard Materials (No. 201405).
Author information
Authors and Affiliations
Contributions
X.Y.K. and C.L. conceived the idea. X.D.X. and C.L. performed the calculations. X.D.X., A.H., M. J., Y.Y.J., X.X.X. and G.M. wrote the manuscript and all authors contributed to revisions.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Xing, X., Hermann, A., Kuang, X. et al. Insights into the geometries, electronic and magnetic properties of neutral and charged palladium clusters. Sci Rep 6, 19656 (2016). https://doi.org/10.1038/srep19656
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep19656
This article is cited by
-
Decrypting the Structural, Electronic and Spectroscopic Properties of GeMgn+(n = 2–12) Clusters: A DFT Study
Journal of Cluster Science (2022)
-
Probing the structural evolution and electronic properties of divalent metal Be2Mgn clusters from small to medium-size
Scientific Reports (2020)
-
Studies on Size Dependent Structures and Optical Properties of CdSeS Clusters
Journal of Cluster Science (2020)
-
Theoretical Study on the Growth Behavior and Photoelectron Spectroscopy of Lanthanum-Doped Silicon Clusters LaSi n 0/− (n = 6–20)
Journal of Cluster Science (2019)
-
Probing the Structural and Electronic Properties of Dirhenium Halide Clusters: A Density Functional Theory Study
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.







 /n) of Pdn0/+/– (n = 2–20) clusters, together with the available theoretical data for comparison.
/n) of Pdn0/+/– (n = 2–20) clusters, together with the available theoretical data for comparison.