Introduction

Recently, searching for Majorana fermions (MFs) in condensed matter systems has attracted much attention1,2,3,4. MFs are their own antiparticles and in condensed matter systems, they can appear as quasiparticle excitations in topological superconductors. Because of their nonlocality and non-Abelian statistics, the zero-energy MFs, also called Majorana zero modes (MZMs) which refer to the zero-energy in-gap excitations, are proposed to be possible to realize fault tolerant topological quantum computation5,6,7. There are several suggestions of physical systems that may support the MZMs8,9,10,11,12,13, among which the one-dimensional p-wave superconducting (SC) model (also called the Kitaev model)5, due to its simplicity and elegance, is the most studied one. Possible realization of the Kitaev model includes quantum wires with a strong spin-orbit coupling (or topologically insulating wires subject to a Zeeman magnetic field) and in proximity to a superconductor11,12. In addition, it can also be realized in cold-atom systems9,14. Other proposals to realize the MZMs include ferromagnetic atomic chains placed in proximity to a conventional superconductor with strong spin-orbit coupling15 and atomic chains with a spatially modulated spin arrangement16,17,18,19,20.

Up to now, most of the theoretical works focus on ideal homogeneous5 or potential-modulated Kitaev chains21,22,23, or Kitaev chains with longer-range hopping and pairing23,24, or even quasi-one-dimensional Kitaev chains with a finite width25,26. Particularly in the periodically potential-modulated case21,22,23, it was found that under time-reversal symmetry, the number of the MZMs can be at most one and if the potential vanishes at certain sites, then the MZM will be very robust and stable for arbitrary strength of the modulation. However, a very important problem unaddressed is the stability and fate of the MZMs under hopping modulation. Naively people may speculate that they are similar under potential and hopping modulations. Whether this is true needs to be verified. Furthermore, if the two modulations result in different topological properties, we want to know what is new the hopping modulation can lead to. Therefore in this work, we investigate the hopping-modulated one-dimensional p-wave SC model which is an extension of the original Kitaev model. We found that, under time-reversal symmetry, the number of the MZMs strongly depends on the period of the modulation. If the period is odd, there can be at most one MZM. However if the period is even, in some parameter regimes the number of the MZMs can be two. Furthermore, the MZMs will disappear as the chemical potential varies no matter the period is odd or even. Therefore the topological properties of the hopping-modulated model are drastically different from those of the potential-modulated one.

Method

We consider a one-dimensional Kitaev p-wave SC model where the hopping is periodically modulated, the Hamiltonian can be written as

where is the periodically modulated hopping integral. Δ ≠ 0 is the p-wave SC pairing gap and V is the chemical potential. Here α = p/q is a rational number with p and q being coprime integers. and , with L being the number of the lattice sites. In addition,

and Q is a unitary matrix that diagonalizes HBdG.

Defining Majorana operators and as

then the quasiparticle operator can be expressed as

with ϕn,i and ψn,i being the amplitudes of the MFs and in the nth eigenstate, respectively. If there exist MZMs, then none of the En in Eq. (1) is zero under periodic boundary condition (PBC) while some of them become zero under open boundary condition (OBC) and the number of the MZMs is the number of the zero En.

Since ti is modulated with a period q (the unit cell is enlarged by q times), therefore under PBC, we have

Using Fourier transform, , . In momentum space, we get

with the nonzero matrix elements of Mk and Δk being and , for . for , while and .

Since we assume ti and Δ in Eq. (1) is real (up to a global phase) throughout the paper, thus Hk respects the time-reversal, particle-hole and chiral symmetries and it can be unitarily transformed to an off-diagonal matrix as26,27,28

here τy is a Pauli matrix acting on the particle-hole space. Then the system belongs to the class BDI which is characterized by the index while the number of the MZMs can be represented by W which is calculated through

In fact, just counts how many times the determinant of Ak crosses the imaginary axis as k evolves from 0 to π/q.

Results and Discussion

First we consider the α = 1/2 case, where t1 = −t2 = −cosδ. Under PBC, we have

Since Det(Ak) is real, W must be zero otherwise Det(Ak) will be zero for some k (which means the bulk energy gap vanishes), therefore, there can be no MZMs.

Generally, the periodic modulation can take many forms. For arbitrary t1 and t2 (t1 ≠ −t2), we have

If V ≠ 0 and , then Det(Ak) will cross the imaginary axis once as k changes from 0 to π/2. In this case, and one MZM exists. Interestingly, at V = 0, we have

In this case, the system can be divided into two separated subsystems A1k and A2k. As k evolves from 0 to π/2, we have

Therefore, if both and are less than zero, then two MZMs will show up in this case and the existence of these two MZMs has been numerically verified (for example, t1 = 0.5, t2 = −0.8 and Δ = 0.5).

For α = 1/3, we have

where t1 = cos(2π/3 + δ), t2 = cos(4π/3 + δ) and t3 = cosδ. In this case,

and (− and + are for k = 0 and π/3, respectively). If , then will cross the imaginary axis exactly once as k evolves from 0 to π/3, which means that and one MZM exists in this case [E1 in Eq. (2) is zero under OBC]. On the contrary, means that the bulk energy gap vanishes and means that Det(Ak) will not cross the imaginary axis as k evolves from 0 to π/3 in such a way that W = 0, in both cases no MZMs exist. 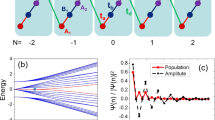Specifically, for δ = (2m + 1)π/6 with m being an integer, we have cos3δ = 0, therefore and no MZMs can exist, irrespective of the values of Δ and V. For example, we set Δ = 1 and L = 1632. In Figs 1 and 2 we plot the energy spectra under OBC and under PBC, respectively. As we can see, at V = 0, MZM exists for any δ, except for δ = π/6, π/2, 5π/6, 7π/6, 3π/2, 11π/6 where the bulk energy gap closes. As V increases, for some δ, MZM vanishes and as δ evolves from 0 to 2π, topologically trivial (without MZM) and nontrivial (with one MZM) phases appear in turn. A typical distribution of the zero-mode MFs is shown in Fig. 3 and we can see that the two MFs and are well separated in real space and are located at the left and right ends, respectively while the actual decay length of these two MFs increases/decreases as the bulk energy gap decreases/increases. Finally when V  > 0.32 where the condition is satisfied, MZM disappears for any δ and there is only topologically trivial phase and indeed for δ = (2m + 1)π/6 with m being an integer, MZMs do not exist for any V.

Figure 1
figure 1

The energy spectra for α = 1/3 under OBC.

Here Δ = 1 and L = 1632. (a–d) are for V = 0, 0.1, 0.2 and 0.3, respectively. Only are plotted.

Full size image
Figure 2
figure 2

Det(Ak=0)Det(Ak=π/3) as a function of δ and V, for α = 1/3 under PBC.

The black solid, red dashed, blue dotted and green dash dotted lines are for V = 0, 0.1, 0.2 and 0.3, respectively. The gray dotted line denotes Det(Ak=0)Det(Ak=π/3) = 0. Here Δ = 1 and L = 1632.

Full size image
Figure 3
figure 3

The distribution of the zero-mode MFs along the one-dimensional lattice for α = 1/3 under OBC.

Here Δ = 1, L = 1632, V = 0.3 and δ = 0.32π, as denoted by the red arrow in Fig. 1(d).

Full size image

For α = 1/4, we have t1 = −t3 = −sinδ and t2 = −t4 = −cosδ. In this case,

At first glance, since Det(Ak) is real, thus, similar to the α = 1/2 case, there should be no MZMs. However, this is not true at V = 0. In the following we set Δ = 1 and L = 1632 as an example. As we can see from Fig. 4, indeed at V = 0.1, there are no MZMs. However at V = 0, MZMs exist for π/4 < δ < 3π/4 and 5π/4 < δ < 7π/4. These MZMs are doubly degenerate [both E1 and E2 in Eq. (2) are zero under OBC] and the distribution of the zero-mode MFs is shown in Fig. 5. The existence of these two MZMs can be explained as follows. At V = 0, we found that the eigenvalues of Hk in Eq. (6) are doubly degenerate, therefore Hk can be divided into two independent subsystems by a unitary transformation as

Figure 4
figure 4

The energy spectra for α = 1/4 under OBC.

Here Δ = 1 and L = 1632. (a) V = 0. (b) V = 0.1. Only are plotted.

Full size image
Figure 5
figure 5

The distribution of the zero-mode MFs along the one-dimensional lattice for α = 1/4 under OBC.

Here Δ = 1, L = 1632, V = 0 and δ = 0.253π. (a) The eigenstate corresponding to E1 = 0. (b) The eigenstate corresponding to E2 = 0.

Full size image

here both H1k and H2k are 4 × 4 matrices while their eigenvalues are exactly the same. The unitary matrix P can be written as

and

At k = 0, while at k = π/4, . If , then both Det(A1k) and Det(A2k) will cross the imaginary axis exactly once as k evolves from 0 to π/4, indicating that there exists one MZM in each subsystem and the number of the MZMs for the whole system is two. Therefore for α = 1/4, at V = 0, the number of the MZMs are either two or zero while at V ≠ 0, there are no MZMs. For general ti, at V ≠ 0, Det(Ak) may not be real and there may exist one MZM. However at V = 0, the system can still be divided into two subsystems. In this case, if the conditions and are satisfied simultaneously, there will be two MZMs.

Furthermore we found that, for general periodic modulation, if the period q is odd, then the number of the MZMs is either zero or one. On the other hand, if q is even, then at V ≠ 0, the number of the MZMs is still zero or one. However at V = 0, the system can always be divided into two independent subsystems and if the conditions

and

are simultaneously satisfied, there will be two MZMs.

In summary, we have studied the number of the MZMs and their stability in the hopping-modulated one-dimensional p-wave SC model. We found that the former strongly depends on the period of the modulation. If the period q is odd, there can be at most one MZM in the system while for an even q, the number of the MZMs can be zero, one and two. The existence of two MZMs can occur only at V = 0, since in this case, Ak in Eq. (7) can always be divided into two independent sub-matrices by a unitary transformation as

At certain conditions, there exists one MZM in each subsystem and the number of the MZMs for the whole system is two. If A1k can be further separated into two subblocks by another unitary transformation R (which is k-independent and real, up to a global k-independent phase) as

then after a tedious calculation we can prove that Det(C1k) and Det(C2k) cannot be complex simultaneously and they can cross the imaginary axis at most once as k varies from 0 to π/q. Therefore, even if A1k can be further separated into two subblocks C1k and C2k, only one of them may host one MZM, making the maximal number of the MZMs in A1k be one. The same argument can be applied to A2k as well. Thus for an even modulation period, there can be at most two MZMs. For the specific modulation form we considered [ti = cos(2πiα + δ) with α = p/q], only at q = 4n can Eqs (19) and (20) be simultaneously satisfied, therefore only in this case can there exist two MZMs. Furthermore, the MZMs will vanish as the chemical potential V varies. In the periodically potential-modulated model considered in Refs. 21, 22, 23, when the time-reversal symmetry is present, there can be at most one MZM and if the potential vanishes at certain sites, then the MZM will be very robust and stable for arbitrary strength of the modulation. Clearly this is not the case in the periodically hopping-modulated model, therefore the topological properties differ drastically between these two models.

At last we would like to emphasize the motivation as well as the physical implications of our study. As we know, exploring various topological properties in different models is of both fundamental and practical importance. From the fundamental point of view, it may help people to understand the mechanism and condition for the existence of the MZMs. As stated in the introduction section, intuitively people may speculate that the topological properties are similar between the hopping-modulated and potential-modulated Kitaev models. However in fact this is not the case as has been demonstrated in our study where both the number and stability of the MZMs differ drastically between these two models and these different behaviors have never been reported before. Furthermore we have demonstrated that, for multiband systems, special caution has to be taken when calculating the number of the MZMs from the index. That is, when the system can be separated into two subsystems, the number of the MZMs may be mistakenly thought to be zero while there are actually two MZMs. On the other hand, from the practical point of view, our work, together with those previous studies concentrating on the potential modulation, may help to guide researchers to fabricate various topological phases with different numbers of the MZMs and to further manipulate them in order to realize topological quantum computation. We expect that our model is most likely to be realized in cold-atom systems and in optical superlattices where the hopping can be adjusted. In solid state devices, the direct modulation of hopping may be difficult. However we notice, the p-wave Kitaev model corresponds to the transverse spin model as29

with , and h = −V/2. Therefore the chemical potential V = 0 can be achieved by setting h = 0 (zero Zeeman field). Furthermore, since t = Jx + Jy and Δ = Jx − Jy, the modulation of hopping may be possible if Jx + Jy varies in space while Jx − Jy is constant. This may be realized in atomic chains with a spatially modulated spin arrangement (see refs. 16, 17, 18, 19, 20). Therefore the ideas in our work are both fundamentally sound and practically applicable.

Additional Information

How to cite this article: Gao, Y. et al. Majorana zero modes in the hopping-modulated one-dimensional p-wave superconducting model. Sci. Rep.5, 17049; doi: 10.1038/srep17049 (2015).