Introduction

Carrier transport in a mesoscopic system is governed by quantum mechanical interference over the spatial phase-coherence range where the interfering phase of carrier waves is determined by the nonlocal response to electromagnetic fields. This nonlocal nature also emerges for the transport of superconducting pair carriers in a laterally extended (width W) superconductor–normal-conductor–superconductor (SNS) proximity junction1,2. Here, the supercurrent density at a position x1 on the interface N/S1 is governed by sum of phase-coherent contributions from positions x2 along the opposite interface N/S2, located within the pair coherence length ξT from x1. For an S1-to-S2 spacing L1 sufficiently shorter than ξT, however, the pair transport depends on the phase difference between the same lateral positions (x1 = x2) only, revealing the local nature of pair coherence3 with highly restricted quasiparticle trajectories in N. Due to this geometric origin of the effect, the local pair coherence has been commonly observed in tunneling Josephson junctions with ultrathin insulating layers. Since a magnetic field spatially modulates the phase of superconducting order, it modifies the Josephson pair current for an extended SNS junction, allowing examination of the locality of pair current modulation.

Fully nonlocal Josephson pair coupling is predicted to show twice the magnetic flux periodicity of the junction critical current for local pair interference4,5 (h/2e). The critical current periodicity of h/e was observed, employing separate extended Josephson junctions of channel length with different L1/W ratios4. A crossover of the Josephson character between local and nonlocal was theoretically proposed, assuming junctions of different physical geometry5. However, since the effective magnetic flux density itself varies in a given magnetic field as L1 and W of a junction change4, due to flux focusing, to trace the nonlocal Josephson characteristics accurately, one needs a scheme of modulating the effective junction aspect ratio for a fixed physical geometry of a junction.

In an SNS proximity junction, the pair coherence can be examined more closely by employing the Andreev interferometry6,7,8,9,10,11,12,13,14,15 (than the Josephson configuration), where the current is biased via the intervening N layer and the potential difference is measured between the N-layer and an S-electrode. In the Andreev interferometry, the detailed carrier coherence effect is revealed in the conductance over a range up to the single-particle phase coherence length lφ (> L1 > ξT). In contrast to studies in the Josephson configuration, in existing pair-coherence studies using Andreev interferometry, the nonlocal character has been commonly observed12,13,15, because the intervening N layer in an Andreev interferometer is bound to be extended. In this study, we attained the local behaviour of the Andreev interferometry by fine tuning ξT marginally close to L1/2. To that end, we adopted an extended S-graphene-S junction consisting of a graphene normal-conductor (N) layer16,17, a single atomic layer of graphite, where backgating allows an effective control of the carrier density and types18 and the range of ξT as adopted in studies of graphene-based Josephson phenomena19,20,21,22,23,24,25. Our graphene-based Andreev interferometer (GAI) also enabled, for the first time, to gate-tune continuously between the local and nonlocal Andreev interference with fixed physical geometry in a device. This accomplishment was only possible by utilising the unparalleled favorable character of graphene such as the absence of band gap at the charge-neutral point (CNP) and the consequent easy gate-tunability of the carrier density. In this sense, graphene incorporating with superconductors provides a truly unique system to meticulously tune and closely examine the locality of pair coherence.

Andreev interferometers adopted in this work consisted of an extended SNS junction with the graphene N layer. We observed Fraunhofer-like magnetoconductance (MC) modulation; with the local (nonlocal) character for a long (short) ξT in highly doped range (near the CNP) in graphene. We continuously adjusted the character of the superconductivity-induced pair coherence in a GAI by changing the effective aspect ratio of the junction along with gate-tuning ξT in the graphene layer. All three GAI devices that we examined exhibited similar features and we present below the data for one particular device. Accurate tracing of the pair-coherence characteristics, in this study, was possible by utilising the highly stable gate tunability of both the carrier density and the corresponding ξT in graphene. The Andreev interferometry adopting graphene offers a convenient and unique platform to investigate the locality of the pair coherence effect.

The GAI consisted of a T-shaped graphene bar (TGB) and an open Al superconducting loop, with the two ends of the Al loop in direct contact with the two arms of the TGB [see Fig. 1(a)]. In the GAI, a propagating electron (hole) could be Andreev-reflected26 as a hole (an electron) at a graphene/Al (G/Al) lateral interface. Two different phase-coherent loops were formed in the device: (i) a closed loop consisting of the open superconducting Al loop and a portion of the TGB and (ii) an Andreev-reflection-mediated closed path for electron- and hole-like carriers inside the phase-coherent region of the graphene layer in the TGB between the two G/Al lateral interfaces. The conductance in the GAI exhibited (i) rapid periodic oscillations with a flux period of h/2e threading the area of loop and (ii) Fraunhofer-type envelop variations of the rapid conductance oscillations, attributed to the magnetic flux threading the closed carrier path in the phase-coherent region of the TGB27. The flux period of the Fraunhofer-type variations gradually shifts between h/2e (local behaviour) and h/e (nonlocal behaviour) along with the gate-dependent variation of ξT. This cannot be due to a change in the flux focusing because the physical geometry of the junction did not vary with gating. The gradual shift of the field periodicity is a consequence of tuning the locality of the superconductivity-induced phase coherence represented by ξT in a GAI.

Figure 1
figure 1

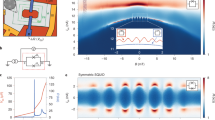
(a) Scanning electron microscopy (SEM) image of the graphene-based Andreev interferometer (GAI), consisting of an open-square Al-loop and a T-shaped monolayer graphene bar within the pair coherence length in the boxed region. The rest part of the graphene below the boxed area acts as measurement leads. (b) Schematic diffusive trajectories of interfering electron- and hole-like partial waves inside the phase-coherent portion of TGB bounded by the dashed line, which extended into the Al wires by the London penetration depth at both G/Al lateral interfaces.

Full size image

Figure 1(a) shows a scanning electron microscopy (SEM) image of the GAI. An open square Al superconducting loop was deposited on the mechanically exfoliated monolayer graphene sheet patterned onto the T-shaped structure (see Methods for details of the fabrication and measurement processes). The carrier mobility in the TGB was ~7,000 cm2/Vs for a backgate voltage Vbg of 50 V at a base temperature of 50 mK. The carrier motion in the TGB was diffusive (L1 > mean free path of le ~ 170 nm; see the supplementary material).

The superconductivity-mediated phase coherence of the carriers was established in the TGB between the two G/Al lateral interfaces. Suppose that an electron is scattered at position P in graphene into two electron-like partial waves. These waves are then Andreev-reflected as hole-like partial waves at different points x1(2) of the left (right) G/Al interface, while each attains the phase of the superconducting order at x1(2). These Andreev-reflected partial waves propagate back to P in a diffusive way to be recombined. The phase value at x1(2) can be expressed as , where ϕ10(20) is the phase at the center of the left (right) G/Al interface and is the phase gradient at the left (right) interface along the x-axis direction.

The phase difference between the ends of the superconducting Al loop was controlled by an external magnetic field with fluxes threading loops (i) and (ii); this induced the above conductance oscillations with a modulated envelope. The total phase difference over loop (i) was Δϕ = ϕ1 − ϕ2 = 2πΦ/Φ0, where Φ0 = h/2e is the flux quantum and Φ is the magnetic flux threading the area, A1 (≈13.3 μm2), enclosed by the centers of the Al-loop wires connected to the left and right G/Al lateral interfaces (Fig. 1(b)). The area of the phase-coherent region (ii), A2, corresponding to the additional phase difference of δϕ, was approximately equal to the TGB area inside the dashed line in Fig. 1(b), which extended into the Al wires by the London penetration depth at both G/Al lateral interfaces12,15. The lower boundary of phase-coherent portion of the TGB also extended by about the electron-hole (e-h) phase coherence length ξT from the bottom ends of the G/Al interfaces. Nonetheless, as shown in the supplementary material, A2 was weakly gate-dependent (~ 0.72 μm2 for Vbg = 50 V).

Results and Discussion

Field dependence of conductance oscillation

Figure 2(a) shows the differential conductance G as a function of the magnetic field B for Vbg = 50 V at T = 50 mK, which resulted from combined contributions of the superconductivity-induced conductance enhancement and the conductance oscillation ΔG below the critical field of Al, Bc = 10.5 mT. The conductance enhancement defined by (GS − GN)/GN was a consequence of the penetration of the Al superconducting order into the graphene at the G/Al interfaces. Here, GS and GN represent the differential conductance of the graphene in contact with the Al ring in the superconducting and normal states, respectively. The maximum of (GS − GN)/GN was ~ 0.18, where G (B = 0 mT) and G (B = 12 mT) were used as GS and GN, respectively. The phase coherence of the GAI over the length L2 was represented by the conductance oscillation of ΔG(B) [ = G(B) − G0(B); G0(B) is the average background value of conductance for a given B]. ΔG(B) consisted of fast h/2e oscillations in Fig. 2(b) and the Fraunhofer-type variations of the envelope in Fig. 2(c). The oscillation period of B in loop (i) was 0.158 mT, which is in good agreement with the value of 0.155 mT estimated from the GAI geometry (see Fig. 1(a)). In Fig. 2(b), ΔG reached its maximum at B = 0, which implies that the graphene did not conserve Berry's phase of π due to the dominant intervalley scattering between the K and K′ valleys28. The maximum amplitude of ΔG (~ 6e2/h) is about an order of magnitude larger than a previous report for a GAI15. We believe that the difference was caused by the difference in the transparency of grpahene/superconductor interfaces and in the geometry of devices. This large conductance oscillation itself was not responsible for the conductance interference behaviour we report. In another device in this study with a much smaller ΔG (~ 0.3e2/h), we obtained similar Fraunhofer behaviour (not shown) as the device with the large value of ΔG.

Figure 2
figure 2

(a) Differential conductance G as a function of the magnetic field B. The solid line is a guide of the averaged background conductance G0. (b) Field dependence of the conductance oscillation ΔG. The oscillation period, ΔB (= 0.158 mT), is in good accordance with the area of the Al loop, 13.3 μm2. The solid line is a fit to multiple Andreev reflection model. (c) Left panel: ΔG vs B at T = 50 mK for different Vbg. Each curve is shifted for clarity. Right panel: the Vbg dependence of resistance of the T-shaped graphene bar, R (≡1/G), with the charge neutral point (CNP) at Vbg = −19 V. (d) Amplitude of the conductance oscillation, ΔG (B = 0), as a function of Vbg. The solid curve is the fit.

Full size image

The ΔG oscillation in Fig. 2(b) is evidently non-sinusoidal. A possible explanation is multiple Andreev reflections at the interfaces. Similar nonsinusoidal conductance modulation has been reported9. Contrary to the case of the report, however, no Josephson-current state was detected between two Al electrodes in our study. From the fast Fourier transform of ΔG(B) in Figure 2(b), we found peaks corresponding to h/2e, h/4e and h/6e oscillations, which led to the field dependence of ΔG as . This relation gives a nice fit to the observed ΔG(B) [solid curve in Figure 2(b)]. Here, the first and third terms (the second term) correspond(s) to the constructive interference of hole (electron) carriers at the point P, which explains the sign of the coefficient of each term, i.e., the constructive interference of hole (electron) carriers implying the diffusion (localisation) of carriers with an increase (a decrease) of the conductance.

The right panel of Fig. 2(c) shows the ambipolar graphene resistance R (≡ 1/G) as a function of Vbg, where Vbg = −19 V is the CNP. ΔG in graphene increased with the electron- or hole-like carrier density by positive or negative gating away from the CNP. The oscillation periods (ΔB) of the ΔG envelope for Vbg = 50, −10, −19, −30 and −50 V were 2.85, ~5, ~6, ~5 and 2.95 mT, respectively. The significant variation in ΔB with the carrier density was caused by the change in the spatial distribution of the e–h phase coherence (between equal and random values of x1 and x2) at the G/Al lateral interfaces (described below), rather than by the change in A2. The weak gate dependence of the phase-coherent TGB area did not induce a significant change in A2 (see the supplementary material).

The e–h phase-coherence length increased with Vbg from the CNP, where is the diffusion constant, is Planck's constant divided by 2π, kB is Boltzmann's constant, Teff(~600 mK) is the effective temperature of the carriers and vF is the Fermi velocity in graphene. ξT was estimated using the relationship ΔG (B = 0) ~ exp(−L2/ξT); ~320 nm for Vbg = 50 V and decreased as Vbg approached the CNP [see Fig. 2(d)]. ΔG (B = 0) remained finite at ~0.1e2/h at the CNP due to e–h puddle-induced fluctuations of the carrier density, which kept ξT finite on the scale of the e–h puddle-induced density fluctuations (a few tens of nm29).

Fraunhofer-type conductance modulation

We now examine Fraunhofer-type variations of the envelope of ΔG, along with the gate-dependent change in the spatial distribution of the e–h phase coherence. We estimate ΔG by adding all of the pair-wise contributions at point P by the carrier partial waves Andreev-reflected at points x1 and x2 at the left and right G/Al interfaces, respectively, with the weighting factor f(x1, x2). Assuming processes involving only a single Andreev reflection from each G/Al interface, the conductance oscillation is given by

Based on the diffusive nature of Andreev reflections4,5, f(x1, x2) can be approximated by a Gaussian-type weighting factor as , which is introduced to simulate the range of pair coherence involved in the interference between carrier partial waves Andreev reflected at x1 in a G/Al interface and x2 in the opposite-side interface. The parameter α simply controls the range of interference. For 2ξT ≈ L1, the overlap of ξT between x1 and x2 is weighted at x1 ≈ x2, thus, the magnitude of the e–h phase coherence at the overlapped region of ξT is much larger than that at the other region and the corresponding effective range of interference is also localised () as shown in Fig. 3(a). Here, we take into account only the time-reversed trajectories before and after the Andreev reflection because other trajectories correspond to strongly differing phases with negligible probability amplitudes. For , however, the magnitude of the e–h phase coherence is strongly suppressed and becomes widely distributed () over the entire range as shown in Fig. 3(b) due to the complete absence of overlap of ξT between x1 and x2. Even in this case, Andreev reflected carrier partial waves retain the macroscopic quantum phase information, obtained from the G/Al interfaces, until they are recombined at the initial scattering point P, because lφ is much longer than L1 and W of the GAI (see the supplementary material).

Figure 3
figure 3

(a) Local pair coherence for 2 ξT ≈ L1. Right panel: f(x1, x2) ≈ δ(x1 − x2), which corresponds to the overlap of ξT between x1 and x2. (b) Nonlocal pair coherence for . Right panel: f(x1, x2) is widely distributed due to the complete absence of overlap of ξT between x1 and x2.

Full size image

Here, we consider two cases: and . For (or 2ξT ≈ L1), f(x1, x2) ≈ δ(x1 − x2), which is 1 for x1 = x2 and 0 otherwise. For this local pair coherence, ΔG(ϕ1, ϕ2) is simplified (see the supplementary material):

where Φ′ = B × A2 is the magnetic flux threading A2. ΔG for Vbg = 50 V, with 2ξT ≈ L1, represents the case of ; the envelope of ΔG, as shown in Fig. 4(a), reveals a typical Fraunhofer-type pattern. The main peak around B = 0 had a zero phase value; the nearest lobes of the pattern had a π phase. This π phase jump alternates between the adjacent lobes [Fig. 4(c)], in agreement with the flux dependence of ΔG given in Eq. (1) [see also the discussion in association with Fig. S5(a)]. The solid curve is the best fit of ΔG to Eq. (2) for Vbg = 50 V.

Figure 4
figure 4

Envelope of ΔG as a function of B for (a) Vbg = 50 V (representing the local pair coherence) and (b) Vbg = −19 V (representing the nonlocal pair coherence) at T = 50 mK. Circular symbols and solid curves represent measured data and the corresponding fits to Eqs. (1) and (2), respectively. Phase information of ΔG vs B is shown for (c) Vbg = 50 V and (d) Vbg = −19 V. Dotted lines denote lobe boundaries of the Fraunhofer-type envelope.

Full size image

For (or ), f(x1, x2) becomes almost constant for all combinations of (x1, x2), leading to nonlocal pair coherence. In this case, an Andreev-reflected hole at a point x1 of the left G/Al interface interferes, with equal probability, with an Andreev-reflected hole at any value of point x2 of the right interface and vice versa12. Thus, ΔG(ϕ1, ϕ2) is given by (see the supplementary material)

ΔG at the CNP, with , represents the case of in Fig. 4(b), where the solid curve is the best fit to Eq. (3). Notably, in comparison with Fig. 4(a), the oscillation period is doubled (ΔΦ′ = 2Φ0). Here, as ΔG is proportional to the square of the sine function, ΔG has a zero phase value for any magnetic field B (Fig. 4(d); see also the discussion in association with Fig. S5(b)), which confirms the sharply contrasting nonlocal interference feature in Fig. 4(b). In the intermediate values of Vbg, the envelope shows a transitional feature between that of Figs. 4(a) and (b) [see Figs. S4(b) and (d) of the supplementary material].

Uniqueness of Fraunhofer-type conductance modulation

Magnetoconductance (MC) modulation has recently been observed in S-graphene-S-type Andreev interferometers15. In the highly doped regime of graphene (but, in contrast to our measurements, the device was still in the nonlocal pair-coherence regime), in the study, the second lobe of the MC envelope was suppressed when the MC signal was ensemble averaged over different scattering configurations for slightly varied backgate voltages. This feature was claimed to indicate that the MC signal, arising from interference of carrier waves Andreev-reflected at graphene/S interfaces, retained sample-specific characters. In the highly doped regime (in the local pair coherence regime) in our devices, the second and higher-order lobes of the Fraunhofer-diffraction-like MC envelope remained robust with respect to ensemble-averaging (see the supplementary material). This indicates that the MC modulation observed in our devices was not caused by the sample-specific interference dominated by impurity scattering in graphene, but was governed by the variation of superconducting phase at G/Al lateral interfaces. For weakened pair coherence near the CNP, the nonlocal character is bound to contain more impurity-induced sample-specific interference, which is not in contradiction to the nonlocal Franuhofer-type MC modulation observed in this study.

Conclusion

The locality of the pair coherence in a normal conductor in contact with superconductors is at the core of studies on the Josephson coupling in mesoscopic scales. We report the first Andreev-interferometry observation of the local behaviour of the pair coherence as well as the common nonlocal behaviour and a continuous tuning between them using GAIs, which was confirmed by the flux period of the Fraunhofer-type conductance variations and the contrasting B-field-dependent phase relationship. It was accomplished by varying the effective L1/W ratio continuously with fixed physical geometry of the devices along with changing the backgate voltages and the resulting ξT in a given device. The local behaviour was confirmed by fine tuning ξT marginally close to L1/2 in the highly doped range of graphene, while the nonlocal behaviour was obtained for ξT much shorter than L1 close to the CNP of graphene. The close examination of the pair coherence characteristics was made possible using the highly stable and effective gate tunability of both the carrier concentration and the corresponding pair coherence length in graphene. GAI provides a convenient and unique platform to investigate the locality of the pair coherence.

Methods

Device fabrication and measurement

A monolayer graphene sheet was exfoliated from a thin graphite flake onto a heavily electron-doped Si substrate capped with a 300-nm-thick oxidation layer. The Si substrate was used as a backgate to modulate the carrier density and types in the graphene. An open-square Al loop of 400 nm in width was directly coupled to the graphene by electron (e)-beam patterning, e-gun deposition and the lift-off technique. The graphene layer was patterned using e-beam lithography and oxygen-plasma etching into a T-shaped structure having a linewidth of 500 nm. The spacing L1 between the two G/Al lateral interfaces was 550 nm. The spacing L2 between the voltage leads B and C was ~0.8 μm. The Al loop was prepared by in-situ sequential deposition of a Ti/Al/Au (7 nm/70 nm/5 nm thick) tri-layer onto the prepatterned e-beam resist. The Ti and Au layers improved the contact at the G/Al interfaces and protected the Al surface from oxidation, respectively. The high transparency of the G/Al interfaces was confirmed by the almost vanishing (<0.1 Ω) contact resistance. With the interferometer mounted in a dilution fridge (Kelvinox; Oxford Instruments), a bias current I was injected into the interferometer in a symmetrical manner between leads A and D. The voltage difference V was monitored between leads B and C [Fig. 1(a)] using a lock-in technique operating at a frequency of 13.3 Hz.